7 Is Less Than -5x
seoindie
Sep 23, 2025 · 5 min read
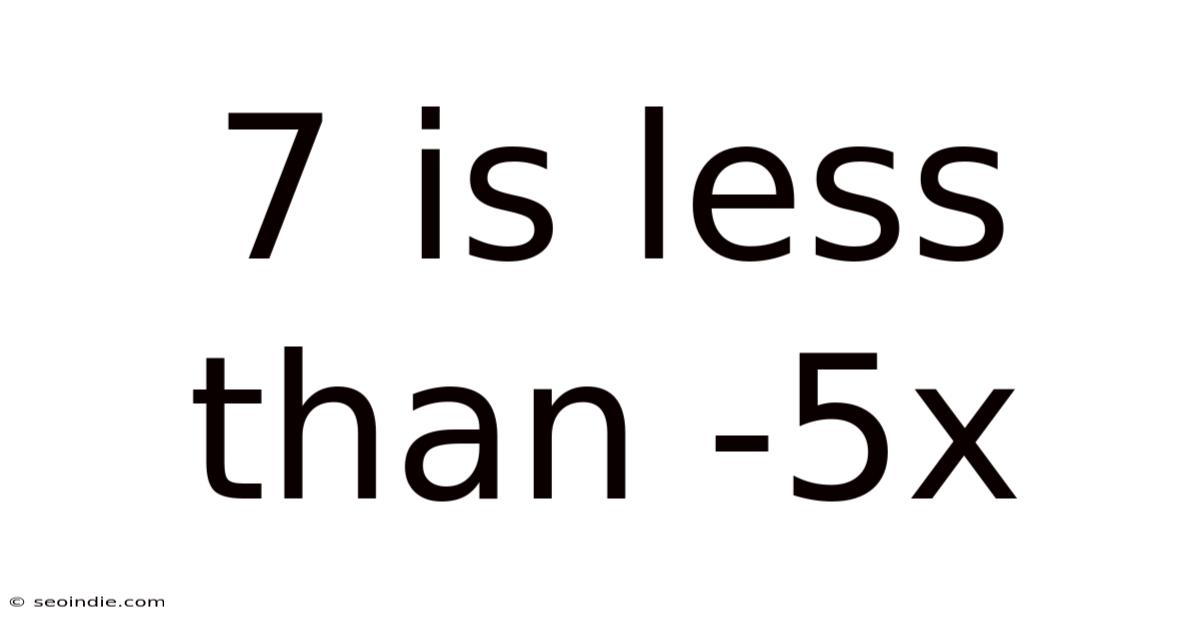
Table of Contents
Solving the Inequality: 7 < -5x
This article will guide you through the process of solving the inequality 7 < -5x, explaining each step clearly and providing additional context to build a strong understanding of algebraic inequalities. We'll explore the principles involved, delve into the solution, and address common misconceptions. This comprehensive guide will equip you with the skills to confidently tackle similar problems.
Introduction: Understanding Inequalities
Before we dive into solving 7 < -5x, let's clarify what an inequality is. Unlike an equation, which uses an equals sign (=) to show that two expressions are equal, an inequality uses symbols like < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to) to show the relationship between expressions that are not necessarily equal. Solving an inequality means finding the range of values for the variable (in this case, x) that makes the inequality statement true.
Steps to Solve 7 < -5x
Our goal is to isolate x on one side of the inequality sign. We'll achieve this by applying inverse operations, remembering a crucial rule: when multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign.
-
Divide Both Sides by -5: To isolate x, we need to divide both sides of the inequality by -5. Remember our crucial rule! Since we're dividing by a negative number, we must reverse the inequality sign.
7 < -5x becomes 7/-5 > x
-
Simplify: Simplifying the fraction, we get:
-1.4 > x
-
Rewrite the Inequality (Optional but Recommended): It's often clearer to rewrite the inequality with the variable on the left side. This doesn't change the meaning, only the presentation. Reversing the inequality gives us:
x < -1.4
Therefore, the solution to the inequality 7 < -5x is x < -1.4. This means any value of x less than -1.4 will make the original inequality true.
Visualizing the Solution: Number Line Representation
A number line is a helpful tool for visualizing the solution to an inequality. To represent x < -1.4 on a number line:
-
Locate -1.4: Find -1.4 on the number line.
-
Draw an Open Circle: Since the inequality is "less than" (not "less than or equal to"), we use an open circle at -1.4. This indicates that -1.4 itself is not included in the solution.
-
Shade to the Left: Shade the number line to the left of -1.4. This represents all the values of x that are less than -1.4.
This visual representation clearly shows the range of values that satisfy the inequality.
Checking the Solution
It's always a good idea to check your solution by substituting a value from the solution set into the original inequality. Let's try x = -2:
7 < -5(-2) 7 < 10
This statement is true, confirming that our solution x < -1.4 is correct. Let's try a value outside the solution set, such as x = -1:
7 < -5(-1) 7 < 5
This statement is false, further validating our solution.
Explanation of the Underlying Mathematical Principles
The process of solving inequalities relies on several key mathematical principles:
-
Additive Inverse: Adding the same number to both sides of an inequality does not change the inequality's truth value. For instance, if a < b, then a + c < b + c.
-
Multiplicative Inverse: Multiplying or dividing both sides of an inequality by the same positive number does not change the inequality's truth value. If a < b, and c > 0, then ac < bc and a/c < b/c.
-
Multiplication/Division by a Negative Number: This is where the crucial rule comes in. Multiplying or dividing both sides of an inequality by a negative number reverses the inequality sign. If a < b and c < 0, then ac > bc and a/c > b/c. This is because multiplying by a negative number essentially reflects the numbers across zero on the number line, changing their relative positions.
Understanding these principles is key to accurately manipulating inequalities and arriving at the correct solution.
Common Mistakes to Avoid
Several common mistakes can arise when solving inequalities:
-
Forgetting to reverse the inequality sign: This is the most frequent error. Remember to reverse the inequality sign whenever you multiply or divide both sides by a negative number.
-
Incorrectly applying order of operations: Always follow the order of operations (PEMDAS/BODMAS) when simplifying expressions on both sides of the inequality.
-
Misinterpreting the solution: Make sure you understand what the solution represents. A number line graph can be very helpful in visualizing the solution set.
Frequently Asked Questions (FAQ)
-
Q: What if the inequality had been 7 > -5x?
A: The process is similar. You would still divide both sides by -5, but again, remember to reverse the inequality sign. The solution would be x > -1.4.
-
Q: Can I solve inequalities with more than one variable?
A: Yes, but the methods become more complex. Techniques such as graphing or linear programming are often used to solve systems of inequalities with multiple variables.
-
Q: What are some real-world applications of inequalities?
A: Inequalities are used extensively in various fields, including:
- Physics: Describing motion, forces, and energy.
- Engineering: Designing structures, circuits, and systems.
- Economics: Modeling supply and demand, profit and loss.
- Computer science: Optimizing algorithms and data structures.
-
Q: What happens if the coefficient of x is zero?
A: If the coefficient of x is zero (-5x becomes 0x), the inequality simplifies to 7 < 0, which is false. There would be no solution in this case.
Conclusion: Mastering Inequalities
Solving inequalities like 7 < -5x involves a systematic approach that requires careful attention to detail. By understanding the underlying principles, following the steps correctly, and avoiding common mistakes, you can confidently solve a wide range of inequalities. Remember the crucial rule about reversing the inequality sign when multiplying or dividing by a negative number, and always check your solution to ensure its accuracy. With practice, you'll develop a strong understanding of inequalities and their applications. This empowers you to confidently tackle more complex mathematical problems and apply this knowledge to various real-world scenarios. Remember that consistent practice is key to mastering this important mathematical skill. Keep practicing, and you will see your understanding and confidence grow.
Latest Posts
Latest Posts
-
Adjectives To Describe A Tree
Sep 23, 2025
-
Meaning Of Non Biodegradable Waste
Sep 23, 2025
-
Verb That Starts With V
Sep 23, 2025
-
How Does Confidence Affect Speeches
Sep 23, 2025
-
1 9 100 As A Percent
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 7 Is Less Than -5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.