657 Thousand Times 1 Thousand
seoindie
Sep 18, 2025 · 6 min read
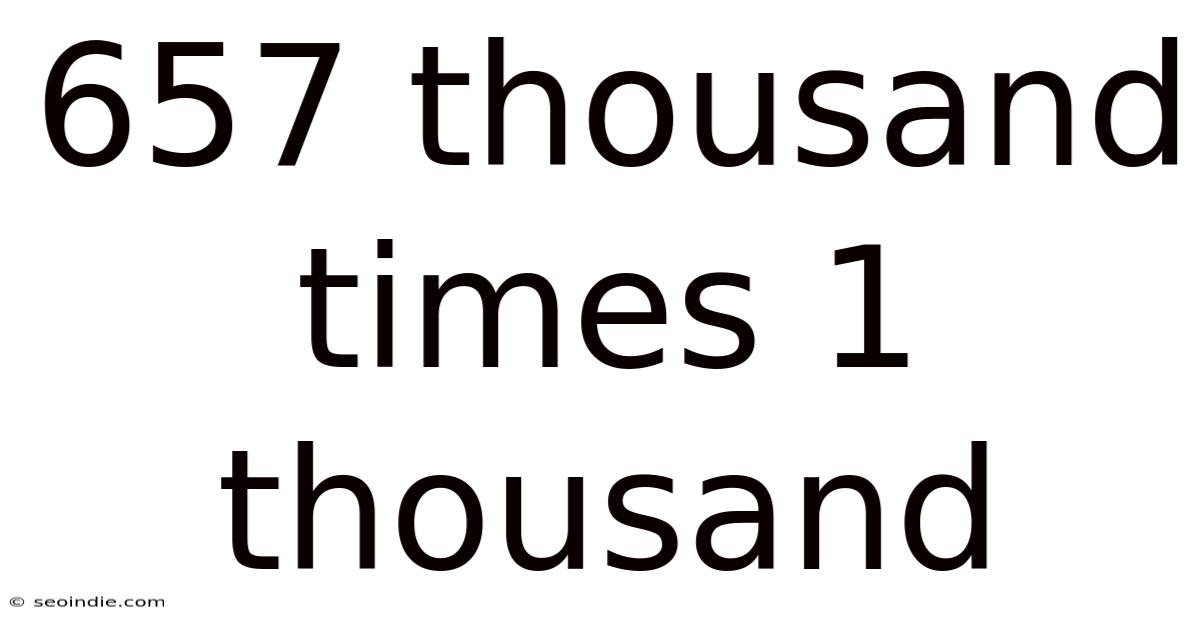
Table of Contents
Decoding 657 Thousand Times 1 Thousand: A Deep Dive into Large Numbers and Their Implications
This article explores the seemingly simple calculation of 657,000 multiplied by 1,000, delving beyond the basic arithmetic to uncover the significance of working with large numbers, their representation, and their applications in various fields. Understanding calculations involving such magnitudes is crucial for comprehending concepts in finance, science, engineering, and many other disciplines. We'll break down the calculation, explore different methods of approaching it, and discuss the implications of dealing with numbers of this scale.
I. The Calculation: 657,000 x 1,000
At its core, the calculation 657,000 x 1,000 is straightforward multiplication. Multiplying by 1,000 is equivalent to shifting the decimal point three places to the right. Therefore:
657,000 x 1,000 = 657,000,000
The result is six hundred fifty-seven million. This seemingly simple calculation serves as a springboard to explore more complex numerical concepts.
II. Understanding Large Numbers and Scientific Notation
Working with large numbers like 657,000,000 often requires specialized tools and notations to enhance readability and manageability. One such tool is scientific notation. Scientific notation expresses numbers as a product of a number between 1 and 10 and a power of 10. In this case:
657,000,000 = 6.57 x 10⁸
This representation significantly simplifies the number, making it easier to compare, manipulate, and understand in various contexts. Scientific notation is particularly useful in fields like astronomy, where distances are often measured in light-years (vast distances requiring numbers with many zeros).
III. Alternative Calculation Methods
While the direct multiplication is straightforward, exploring alternative methods can deepen our understanding of the underlying mathematical principles. Let's consider a couple of approaches:
- Distributive Property: We can break down 657,000 into smaller, more manageable parts. For example: 657,000 = 600,000 + 50,000 + 7,000 Then, we multiply each part by 1,000: (600,000 x 1,000) + (50,000 x 1,000) + (7,000 x 1,000) = 600,000,000 + 50,000,000 + 7,000,000 = 657,000,000
This method highlights the distributive property of multiplication, showing how it works with larger numbers.
- Using Logarithms: While less intuitive for this specific calculation, logarithms provide a powerful tool for simplifying multiplication, especially with very large or very small numbers. Logarithms transform multiplication into addition. By finding the logarithms of 657,000 and 1,000, adding them, and then finding the antilogarithm, we can arrive at the same result. However, for this specific case, direct multiplication is far more efficient.
IV. Real-World Applications: Where Do We Encounter Such Numbers?
Numbers of this magnitude are frequently encountered in many real-world situations:
-
Finance: National budgets, gross domestic product (GDP) figures, and the total market capitalization of major corporations often involve billions. Understanding calculations involving such numbers is essential for financial analysis and economic modeling.
-
Science: In fields like physics and astronomy, dealing with extremely large numbers is commonplace. For example, the number of atoms in a mole of a substance (Avogadro's number, approximately 6.022 x 10²³) or the distance to distant stars are expressed in astronomically large numbers.
-
Engineering: Large-scale engineering projects, such as dam construction, require dealing with massive quantities of materials and energy. Calculations involving such quantities necessitate a clear understanding of working with large numbers.
-
Population Studies: Global population numbers, demographic projections, and population densities often involve billions of individuals. Analyzing these figures requires handling large-scale numerical data.
-
Computer Science: In computer science, data sizes are often measured in gigabytes (GB) and terabytes (TB), representing billions and trillions of bytes. Managing and processing this data effectively necessitates an understanding of large numbers.
V. Error Handling and Significant Figures
When dealing with large numbers, it's crucial to consider the impact of rounding errors and significant figures. While the calculation 657,000 x 1,000 yields a precise result, real-world data often involves approximations. If the initial number 657,000 was itself a rounded figure, the final result should reflect the corresponding uncertainty. Understanding significant figures ensures that the final answer doesn't suggest a higher level of accuracy than the input data allows.
VI. Visualizing Large Numbers
One of the challenges in working with such large numbers is visualizing their scale. While we can easily grasp the magnitude of a few hundred or even a few thousand, comprehending billions becomes significantly more difficult. Several techniques can help visualize these magnitudes:
-
Analogies: Comparing large numbers to familiar concepts can aid in understanding their scale. For instance, we could compare 657 million to the approximate population of a large country or the number of grains of sand on a beach (although the exact numbers vary greatly).
-
Data Visualization: Graphical representations like bar charts, pie charts, or maps can make large numerical data more accessible and easier to understand. Visualizing the data allows for a more intuitive grasp of its proportions and relationships.
VII. Further Exploration: Beyond Simple Multiplication
The seemingly simple calculation of 657,000 x 1,000 opens doors to more complex mathematical concepts. Consider the following extensions:
-
Exponentiation: What if we raised 657,000 to the power of 1,000 (657,000¹⁰⁰⁰)? This would result in an unimaginably large number, requiring specialized tools and mathematical techniques to handle.
-
Compounding Growth: In finance, concepts like compound interest involve repeatedly multiplying a number by a factor. Understanding how this works with larger initial amounts helps in comprehending the power of compounding over time.
-
Large-Scale Simulations: Many scientific and engineering simulations involve working with extremely large datasets and performing calculations on them. The efficiency of these calculations depends on techniques for handling large numbers effectively.
VIII. Frequently Asked Questions (FAQ)
-
Q: What is the best way to calculate 657,000 x 1,000?
- A: The simplest and most efficient method is to shift the decimal point three places to the right, adding three zeros: 657,000,000.
-
Q: Why is scientific notation important when dealing with large numbers?
- A: Scientific notation simplifies the representation of large numbers, making them easier to write, compare, and manipulate, especially in scientific and engineering contexts.
-
Q: How can I visualize the size of 657 million?
- A: Try relating it to familiar concepts like the population of a large country or the number of items in a massive collection. Visual aids, such as graphs and charts, can also be beneficial.
-
Q: Are there any potential errors when working with large numbers?
- A: Yes, rounding errors and considerations regarding significant figures are crucial when dealing with large numbers based on real-world data. The accuracy of the input data directly affects the accuracy of the output.
IX. Conclusion
The seemingly straightforward calculation of 657,000 x 1,000 serves as a gateway to understanding the complexities of working with large numbers. From mastering fundamental arithmetic to utilizing advanced notations like scientific notation and handling potential errors, proficiency in handling large numbers is crucial in various fields. Beyond the basic calculation, this exploration has revealed the broader implications and applications of large numbers in finance, science, engineering, and beyond. Understanding these concepts equips us with essential tools for navigating a world increasingly reliant on large-scale data and complex numerical analyses. The journey from a simple multiplication problem to a deep understanding of numerical scale highlights the interconnectedness of seemingly disparate fields and the power of mathematical reasoning.
Latest Posts
Latest Posts
-
Lcm Of 36 And 45
Sep 18, 2025
-
Hectares In A Square Mile
Sep 18, 2025
-
Baso4 Is Insoluble In Water
Sep 18, 2025
-
The Square Root Of 29
Sep 18, 2025
-
Define Geographic Isolation In Biology
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 657 Thousand Times 1 Thousand . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.