Lcm Of 36 And 45
seoindie
Sep 18, 2025 · 5 min read
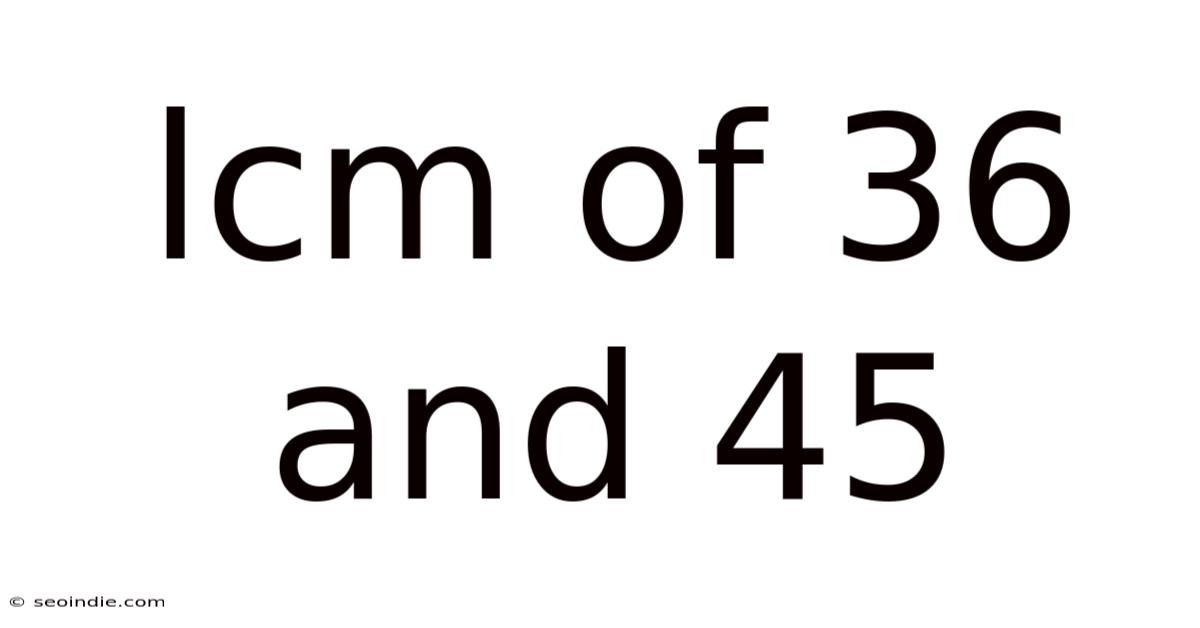
Table of Contents
Finding the LCM of 36 and 45: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a strong foundation in number theory and problem-solving. This article will explore the LCM of 36 and 45 in detail, examining various approaches, explaining the mathematical principles involved, and addressing common questions. We'll delve beyond just the answer to truly grasp the significance of LCMs in mathematics and beyond.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events.
For instance, if you have two gears rotating, understanding their LCM helps determine when they will both return to their starting positions simultaneously. Similarly, in scheduling tasks that repeat at different intervals, the LCM determines the time when all tasks will align again.
Method 1: Listing Multiples
The most straightforward method, although less efficient for larger numbers, involves listing the multiples of each number until a common multiple is found.
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360, ...
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360, ...
Notice that 180 and 360 appear in both lists. The smallest common multiple is 180. Therefore, the LCM(36, 45) = 180. This method is fine for smaller numbers but becomes cumbersome for larger ones.
Method 2: Prime Factorization
This method is more efficient and is based on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
-
Find the prime factorization of each number:
- 36 = 2² × 3²
- 45 = 3² × 5
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3² = 9.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
LCM(36, 45) = 2² × 3² × 5 = 4 × 9 × 5 = 180
This method is far more efficient than listing multiples, especially for larger numbers. It provides a systematic approach to finding the LCM, directly leveraging the fundamental building blocks of numbers – prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. There's a formula that connects them:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where |a × b| represents the absolute value of the product of a and b.
-
Find the GCD of 36 and 45 using the Euclidean algorithm:
- Divide the larger number (45) by the smaller number (36): 45 ÷ 36 = 1 with a remainder of 9.
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (9): 36 ÷ 9 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 9. Therefore, GCD(36, 45) = 9.
-
Apply the formula:
LCM(36, 45) = (36 × 45) / 9 = 1620 / 9 = 180
This method is also very efficient and highlights the interconnectedness between LCM and GCD. The Euclidean algorithm, used to find the GCD, is a powerful and elegant method for finding the greatest common divisor of two integers.
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It finds applications in numerous fields, including:
- Scheduling: Determining when events that repeat at different intervals will coincide. For example, finding when two buses with different schedules will arrive at the same stop simultaneously.
- Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
- Music: Calculating rhythmic patterns and harmonies in music composition. The LCM helps in understanding when different rhythmic patterns will align.
- Physics: Solving problems involving periodic phenomena like oscillations and waves.
- Computer Science: In algorithms and data structures, LCM finds applications in various optimization problems.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. The GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder. They are inversely related; as one increases, the other decreases.
Q: Can the LCM of two numbers be equal to one of the numbers?
A: Yes, if one number is a multiple of the other. For example, LCM(6, 12) = 12.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor present, and multiply them together. You can also use the iterative approach, finding the LCM of the first two numbers, then finding the LCM of that result and the third number, and so on.
Q: Why is the prime factorization method preferred for larger numbers?
A: The listing multiples method becomes impractical for larger numbers as the list of multiples grows exponentially. The prime factorization method provides a more efficient and systematic approach, especially when dealing with large numbers with many factors.
Conclusion
Finding the LCM of 36 and 45, as we've demonstrated, isn't merely about getting the answer (180). It's about understanding the underlying principles of number theory, exploring different computational methods, and appreciating the broader applications of this fundamental concept. By mastering the techniques discussed here – listing multiples, prime factorization, and the GCD method – you equip yourself with valuable tools for tackling more complex mathematical problems across various disciplines. The ability to efficiently find the LCM is a cornerstone of mathematical literacy and problem-solving skills. Remember that the most important aspect is not just memorizing formulas but understanding the why behind the calculations, leading to a deeper appreciation of the beauty and logic within mathematics.
Latest Posts
Latest Posts
-
3 Letter Words With Meaning
Sep 19, 2025
-
How To Write Story Dialogue
Sep 19, 2025
-
Gcf Of 36 And 20
Sep 19, 2025
-
500 Sq Meters To Feet
Sep 19, 2025
-
What Is Roman Numeral Xlviii
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 36 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.