Gcf Of 21 And 28
seoindie
Sep 22, 2025 · 7 min read
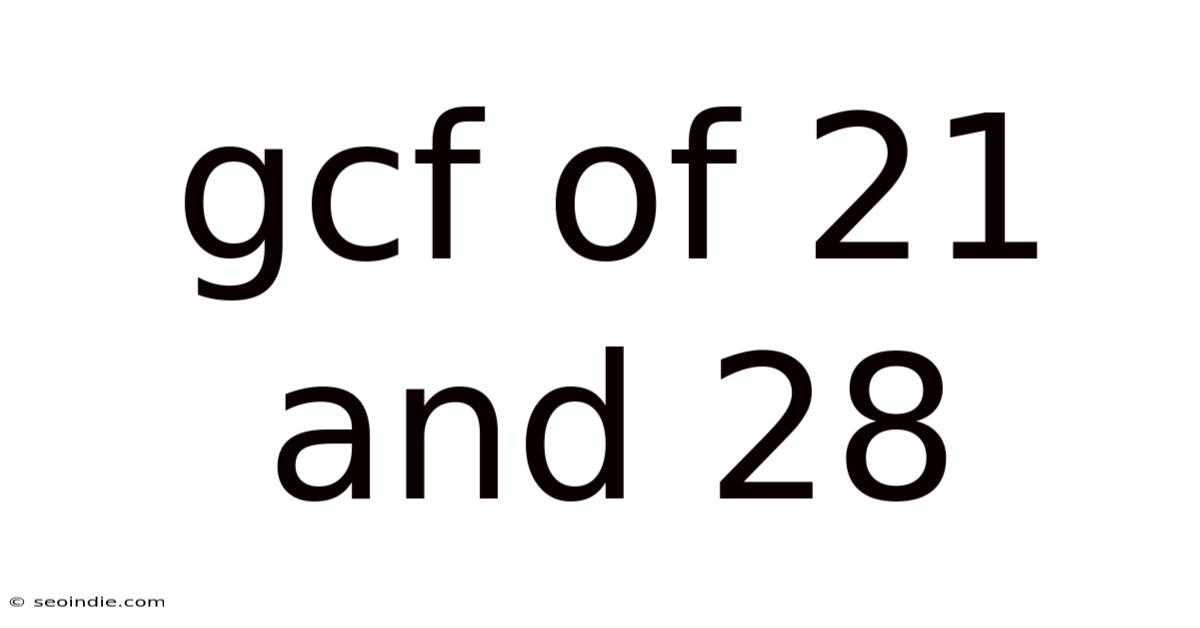
Table of Contents
Finding the Greatest Common Factor (GCF) of 21 and 28: A Deep Dive
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with wide-ranging applications. This article will explore how to find the GCF of 21 and 28, explaining several methods in detail, providing a deeper understanding of the underlying mathematical principles, and answering frequently asked questions. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and even tackling more advanced mathematical concepts. Let's dive in!
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both (or all) numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest number that appears in both lists is 6, so the GCF of 12 and 18 is 6. This article focuses on finding the GCF of 21 and 28.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 21 and 28, involves listing all the factors of each number and identifying the largest common factor.
Factors of 21: 1, 3, 7, 21 Factors of 28: 1, 2, 4, 7, 14, 28
Comparing the two lists, we see that the common factors are 1 and 7. The greatest of these common factors is 7. Therefore, the GCF of 21 and 28 is 7.
This method is simple and intuitive, making it ideal for beginners. However, it becomes less efficient as the numbers get larger. Imagine trying to list all the factors of 147 and 252!
Method 2: Prime Factorization
Prime factorization is a more robust method that works effectively for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 21 and 28:
- 21: 3 x 7 (3 and 7 are both prime numbers)
- 28: 2 x 2 x 7 (2 and 7 are prime numbers; 2 x 2 is often written as 2²)
Now, we identify the common prime factors. Both 21 and 28 share a factor of 7. The GCF is the product of the common prime factors raised to the lowest power they appear in either factorization. In this case, the only common prime factor is 7, and it appears to the power of 1 in both factorizations. Therefore, the GCF of 21 and 28 is 7.
This method is more efficient than listing factors, particularly for larger numbers, as it systematically breaks down the numbers into their fundamental building blocks.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 21 and 28:
- Start with the larger number (28) and the smaller number (21).
- Subtract the smaller number from the larger number: 28 - 21 = 7
- Replace the larger number with the result (7) and keep the smaller number (21). Now we have 21 and 7.
- Repeat the subtraction: 21 - 7 = 14
- Now we have 14 and 7.
- Repeat: 14 - 7 = 7
- Now we have 7 and 7. Both numbers are equal, therefore, the GCF is 7.
The Euclidean algorithm provides a systematic and efficient way to determine the GCF, regardless of the size of the numbers. It's a powerful tool in number theory and has significant practical applications in computer science and cryptography.
Visual Representation: Venn Diagram
We can visualize the GCF using a Venn diagram. The Venn diagram represents the factors of each number as circles, with overlapping areas representing common factors.
[Imagine a Venn diagram here. One circle labeled "Factors of 21" containing 1, 3, 7, 21. Another circle labeled "Factors of 28" containing 1, 2, 4, 7, 14, 28. The overlapping area contains 1 and 7.]
The overlapping area represents the common factors. The largest number in the overlapping area is the GCF, which, as we've seen, is 7. This visual representation aids understanding, particularly for students who benefit from visual learning.
Mathematical Explanation: Divisibility Rules and Prime Factorization
The GCF is deeply connected to the concepts of divisibility and prime factorization. Understanding these concepts strengthens the foundation of number theory.
Divisibility rules offer shortcuts for determining if a number is divisible by another. For example:
- A number is divisible by 2 if it's an even number.
- A number is divisible by 3 if the sum of its digits is divisible by 3.
- A number is divisible by 5 if it ends in 0 or 5.
- A number is divisible by 7 doesn't have a simple rule, but we can use long division.
Prime factorization, as explained earlier, involves expressing a number as a product of prime numbers. This decomposition is unique for every number (Fundamental Theorem of Arithmetic). The GCF is easily obtained from the prime factorization by selecting the common prime factors and multiplying them together.
Applications of GCF
The GCF has numerous applications across various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 21/28 can be simplified by dividing both the numerator and denominator by their GCF (7), resulting in the equivalent fraction 3/4.
-
Algebra: The GCF is used to factor algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and solving equations.
-
Geometry: GCF is used in problems related to area, volume and measurement. For instance, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 21 units by 28 units.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for numerous theorems and algorithms.
-
Cryptography: GCF and related concepts play a crucial role in modern cryptography, particularly in public key cryptography.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be greater than the smaller number?
A: No. The GCF is always less than or equal to the smaller of the two numbers.
Q: Is there a limit to how large the numbers can be for which we can find the GCF?
A: Theoretically, no. The Euclidean algorithm and prime factorization methods work for numbers of any size, although computational limitations might exist for extremely large numbers.
Q: What are some real-world examples of using GCF?
A: Imagine you're making gift bags for a party. You have 21 candies and 28 cookies. You want to put the same number of candies and cookies in each bag without any leftovers. The GCF (7) tells you can make 7 bags, each with 3 candies and 4 cookies.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with practical applications in various fields. This article explored several methods—listing factors, prime factorization, and the Euclidean algorithm—to determine the GCF of 21 and 28, highlighting their strengths and limitations. Understanding GCFs not only helps in solving mathematical problems but also strengthens your grasp of fundamental number theory concepts. Mastering this concept opens doors to a deeper appreciation of the beauty and logic inherent in mathematics. Remember that practice is key to solidifying your understanding and improving your efficiency in finding the GCF of any two numbers.
Latest Posts
Latest Posts
-
Difference Between Ester And Ether
Sep 22, 2025
-
How Much Is 7 5 Cm
Sep 22, 2025
-
What Is 34 Divisible By
Sep 22, 2025
-
Example Of A Compressional Wave
Sep 22, 2025
-
Relationship Between Energy And Wavelength
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 21 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.