4 Square Root Of 81
seoindie
Sep 24, 2025 · 6 min read
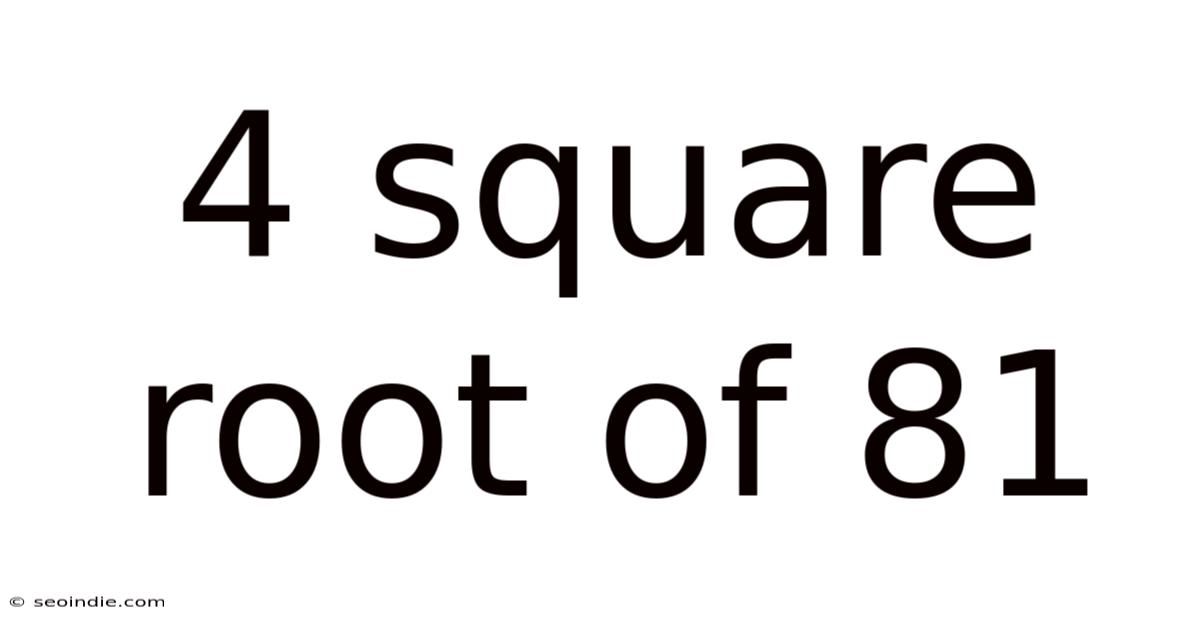
Table of Contents
Unveiling the Mysteries of the Fourth Root of 81: A Deep Dive into Radical Expressions
Understanding the fourth root of 81 might seem like a simple mathematical problem, but it opens a door to a fascinating world of radical expressions, exponents, and their practical applications. This comprehensive guide will not only solve the problem but also explore the underlying concepts, providing you with a solid foundation in this area of mathematics. We'll delve into the meaning of roots, the relationship between roots and exponents, and explore various methods for solving similar problems. This will equip you to tackle more complex problems confidently and appreciate the elegance of mathematical principles.
Introduction: What Does the Fourth Root Mean?
Before we tackle the specific problem of finding the fourth root of 81 (⁴√81), let's establish a clear understanding of what a root represents. In simpler terms, finding the nth root of a number 'x' means finding a number that, when multiplied by itself n times, equals 'x'. For example, the square root (²√) of 9 is 3 because 3 x 3 = 9. Similarly, the cube root (³√) of 8 is 2 because 2 x 2 x 2 = 8. Extending this logic, the fourth root (⁴√) of a number is a value that, when multiplied by itself four times, results in the original number.
Therefore, finding ⁴√81 means finding a number that, when multiplied by itself four times, equals 81.
Methods for Solving ⁴√81
There are several approaches to solving this problem, each offering valuable insights into the underlying mathematical principles:
1. Prime Factorization Method:
This method is particularly useful for understanding the structure of the number and is often the most intuitive approach for beginners. Let's break down 81 into its prime factors:
- 81 = 9 x 9
- 9 = 3 x 3
Therefore, 81 can be written as 3 x 3 x 3 x 3, or 3⁴. Since the fourth root is the inverse operation of raising to the power of four, we can see directly that:
⁴√81 = ⁴√(3⁴) = 3
This method highlights the fundamental relationship between roots and exponents. It visually demonstrates how repeated multiplication (exponentiation) and finding the root are inverse operations.
2. Exponent Rules and Simplification:
This method leverages the properties of exponents to simplify the expression. Remember that the nth root of a number can be represented as that number raised to the power of 1/n. So, ⁴√81 can be written as 81^(1/4).
Using the property that (aᵐ)ⁿ = aᵐⁿ, we can rewrite 81 as 3⁴. Thus:
⁴√81 = 81^(1/4) = (3⁴)^(1/4) = 3^(4*(1/4)) = 3¹ = 3
This method reinforces the connection between fractional exponents and roots, emphasizing their mathematical equivalence.
3. Trial and Error (for smaller numbers):
While not the most efficient method for larger numbers, trial and error can be a helpful approach for smaller numbers like 81. We can systematically test different numbers to see if their fourth power equals 81.
- 1⁴ = 1
- 2⁴ = 16
- 3⁴ = 81
Therefore, we find that 3 is the fourth root of 81. This method, although simple, builds an intuitive understanding of what the fourth root represents.
Understanding the Concept of Multiple Roots
While the primary focus has been on finding the principal root, it is crucial to mention the concept of multiple roots, particularly in the context of even roots (like square roots and fourth roots).
For even roots, there are always two possible solutions (one positive and one negative). In the case of ⁴√81, while 3 is the principal (positive) root, (-3) is also a solution because (-3) x (-3) x (-3) x (-3) = 81.
However, when dealing with equations or real-world applications, the principal root (the positive solution) is generally used unless specifically stated otherwise.
Expanding the Concept: Higher-Order Roots and More Complex Expressions
The principles discussed above can be extended to solve problems involving higher-order roots and more complex expressions. For example:
-
Finding the fifth root of 32 (⁵√32): This involves finding a number that, when multiplied by itself five times, equals 32. Using prime factorization, we find that 32 = 2⁵, so ⁵√32 = 2.
-
Solving equations involving fourth roots: An equation like x⁴ = 16 can be solved by taking the fourth root of both sides: x = ⁴√16 = 2 (or x = -2).
-
Dealing with expressions containing both roots and exponents: An expression like (⁴√16)² can be simplified by first calculating the fourth root of 16 (which is 2) and then squaring the result (2² = 4).
Practical Applications of Roots
Understanding roots and radical expressions is not just a matter of abstract mathematical concepts. They find widespread applications in various fields, including:
-
Engineering: Calculations involving volume, area, and dimensions often involve roots. For example, finding the side length of a cube given its volume requires calculating a cube root.
-
Physics: Many physical phenomena are described by equations involving roots, including calculations related to wave motion, oscillations, and gravitational forces.
-
Finance: Compound interest calculations and determining the rate of return on investments can involve the use of roots.
-
Computer Graphics: Roots are employed in algorithms for generating curves and surfaces, crucial in creating realistic images and 3D models.
-
Statistics: Calculating standard deviation, a measure of data dispersion, often involves using square roots.
Frequently Asked Questions (FAQs)
Q: Is there only one answer to the fourth root of 81?
A: While the principal root is 3, there are actually two real roots: 3 and -3, as (-3)⁴ = 81.
Q: How can I calculate higher-order roots without using a calculator?
A: Prime factorization is a useful technique for simpler numbers. For larger or more complex numbers, numerical methods or logarithms might be necessary.
Q: What if the number inside the radical is negative?
A: For even roots (like square roots, fourth roots, etc.), the root of a negative number is not a real number. It results in an imaginary number, typically represented using the imaginary unit i, where i² = -1.
Conclusion: Mastering Roots – A Foundation for Mathematical Proficiency
Understanding the fourth root of 81, and the broader concept of roots and radical expressions, provides a foundational understanding of essential mathematical principles. This knowledge is not just about solving equations; it's about grasping the interconnectedness of different mathematical operations and appreciating their practical applications in diverse fields. By mastering these concepts, you build a stronger mathematical foundation, equipping yourself to tackle more complex problems and appreciate the elegance and power of mathematics. The journey to mathematical proficiency is built on understanding fundamental concepts like roots, and this exploration of the fourth root of 81 serves as an excellent stepping stone on that journey. Remember to practice regularly and explore different methods to solidify your understanding.
Latest Posts
Latest Posts
-
Civil Services Examination Age Limit
Sep 24, 2025
-
Chemistry Reactions In Everyday Life
Sep 24, 2025
-
Word That Ends In Exs
Sep 24, 2025
-
Gcf Of 15 And 6
Sep 24, 2025
-
How Deep Is 50 Metres
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Square Root Of 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.