Gcf Of 15 And 6
seoindie
Sep 24, 2025 · 7 min read
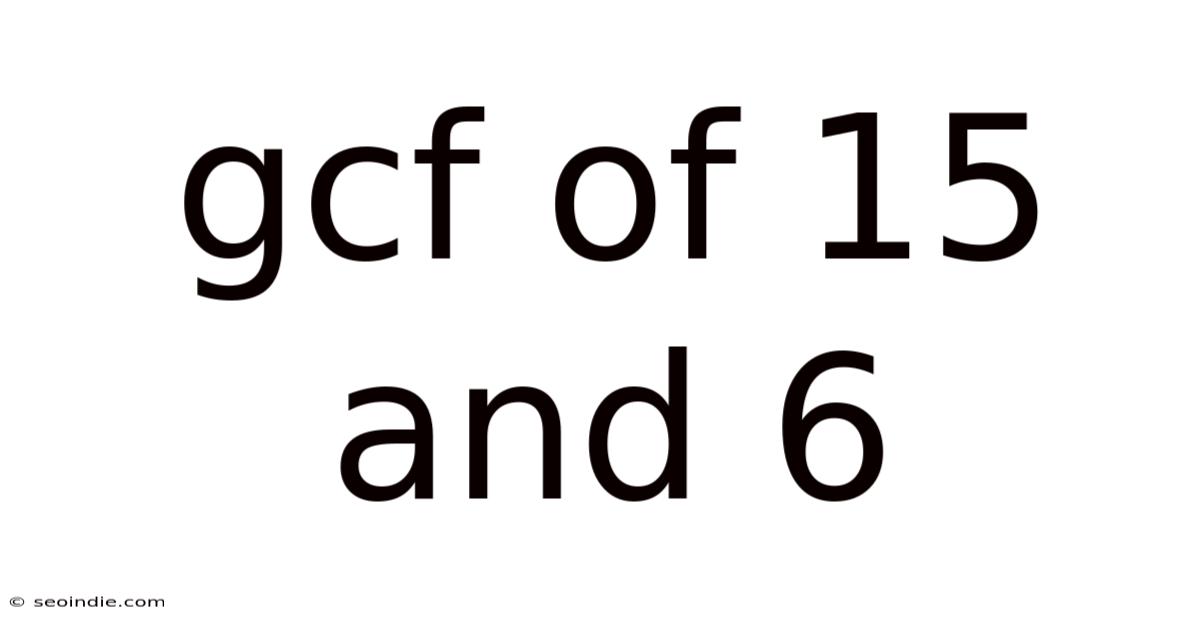
Table of Contents
Finding the Greatest Common Factor (GCF) of 15 and 6: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This seemingly simple task underpins more complex mathematical operations and is crucial for simplifying fractions, solving algebraic equations, and understanding number theory. This article will delve into the various methods for finding the GCF of 15 and 6, providing a comprehensive understanding of the process and its underlying principles. We'll explore different approaches, explain the reasoning behind each step, and address frequently asked questions. By the end, you'll not only know the GCF of 15 and 6 but also possess the tools to find the GCF of any pair of numbers.
Understanding the Concept of Greatest Common Factor (GCF)
Before we dive into the methods, let's clarify what the GCF actually is. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. For example, the factors of 6 are 1, 2, 3, and 6. The factors of 15 are 1, 3, 5, and 15. The common factors of 6 and 15 are 1 and 3. The greatest of these common factors is 3. Therefore, the GCF of 15 and 6 is 3.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers like 15 and 6.
-
List the factors of each number:
- Factors of 6: 1, 2, 3, 6
- Factors of 15: 1, 3, 5, 15
-
Identify the common factors: Look for the numbers that appear in both lists. In this case, the common factors are 1 and 3.
-
Determine the greatest common factor: The largest number among the common factors is the GCF. Therefore, the GCF of 15 and 6 is 3.
This method is simple and intuitive, making it ideal for beginners. However, it becomes less efficient when dealing with larger numbers, as listing all the factors can be time-consuming.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works efficiently for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Find the prime factorization of each number:
- 6 = 2 x 3
- 15 = 3 x 5
-
Identify common prime factors: Look for the prime factors that appear in both factorizations. In this case, the only common prime factor is 3.
-
Multiply the common prime factors: Multiply the common prime factors together to find the GCF. Since the only common prime factor is 3, the GCF of 15 and 6 is 3.
This method is more systematic and efficient than listing factors, especially when dealing with larger numbers. It provides a deeper understanding of the number's structure and is a cornerstone of many advanced mathematical concepts.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
-
Divide the larger number by the smaller number and find the remainder:
- 15 ÷ 6 = 2 with a remainder of 3
-
Replace the larger number with the smaller number and the smaller number with the remainder:
- Now we find the GCF of 6 and 3.
-
Repeat the process:
- 6 ÷ 3 = 2 with a remainder of 0
-
The GCF is the last non-zero remainder: Since the remainder is 0, the GCF is the previous remainder, which is 3.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, regardless of the size of the numbers involved. It's a fundamental algorithm in computer science and number theory.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method highlights the fundamental building blocks of numbers. Understanding prime factorization helps us appreciate the unique composition of each number. For instance, the prime factorization of 6 (2 x 3) tells us that 6 is composed of one factor of 2 and one factor of 3. Similarly, the prime factorization of 15 (3 x 5) reveals its composition of one factor of 3 and one factor of 5. By comparing these factorizations, we immediately identify the common factor, 3.
This method's significance extends beyond simply finding the GCF. Prime factorization is crucial in:
- Simplifying fractions: To simplify a fraction, we find the GCF of the numerator and denominator and divide both by it.
- Solving algebraic equations: GCF is used in factoring polynomials, a critical step in solving many algebraic equations.
- Cryptography: Prime factorization plays a crucial role in modern cryptography, particularly in RSA encryption, which relies on the difficulty of factoring large numbers into their prime components.
- Number theory: Prime factorization is a central concept in number theory, a branch of mathematics that explores the properties of numbers.
Understanding prime factorization provides a deeper understanding of the structure and properties of numbers, extending far beyond the simple task of finding the GCF.
Why is finding the GCF important? Real-world applications
The GCF is more than just an abstract mathematical concept; it has numerous practical applications in various fields:
-
Measurement and Division: Imagine you have two pieces of ribbon, one 15 inches long and the other 6 inches long. You want to cut them into identical smaller pieces of the greatest possible length. The GCF (3 inches) tells you the longest length you can cut them into without any leftover ribbon.
-
Recipe Scaling: Suppose a recipe calls for 15 ounces of flour and 6 ounces of sugar. To reduce the recipe, you need to find the greatest common divisor to scale down proportionally while maintaining the correct ratio of ingredients. The GCF of 15 and 6 (3) tells you the recipe can be divided by 3.
-
Data Organization: When dealing with data sets or arrays, the GCF can help you arrange elements into equally sized groups, maximizing efficiency and minimizing waste.
-
Geometry: GCF is applied in geometric problems involving area and perimeter calculations, simplifying problems and finding common dimensions.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the Euclidean Algorithm be used for more than two numbers?
A: Yes, but you need to apply it iteratively. First, find the GCF of two numbers, then find the GCF of the result and the third number, and so on.
Q: Are there any other methods to find the GCF?
A: While the methods discussed here are the most common and efficient, other less frequently used techniques exist. However, the methods described above offer a comprehensive and practical approach to solving most GCF problems.
Q: Why is prime factorization considered a more powerful method than simply listing factors?
A: Prime factorization provides a structural understanding of the numbers. It's more efficient for larger numbers because it directly identifies the fundamental building blocks, avoiding the need to exhaustively list all factors, which becomes impractical with larger numbers.
Conclusion
Finding the greatest common factor (GCF) of 15 and 6, which is 3, is a fundamental concept with wide-ranging applications. We explored three methods: listing factors, prime factorization, and the Euclidean algorithm. While listing factors is straightforward for smaller numbers, prime factorization and the Euclidean algorithm provide more efficient and systematic approaches for larger numbers. Understanding these methods not only helps solve GCF problems but also provides a deeper understanding of number theory and its practical applications in various fields. Remember, mastering the GCF is a stepping stone to more advanced mathematical concepts and problem-solving skills. So, practice these methods, and you'll find yourself confidently tackling more complex mathematical challenges!
Latest Posts
Latest Posts
-
Differentiate Between Resistance And Resistivity
Sep 24, 2025
-
What Is Shine Dalgarno Sequence
Sep 24, 2025
-
Unit Of Measurement For Torque
Sep 24, 2025
-
Animals With Five Letter Names
Sep 24, 2025
-
How To Calculate Linear Speed
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 15 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.