2 3 Equals What Percent
seoindie
Sep 16, 2025 · 5 min read
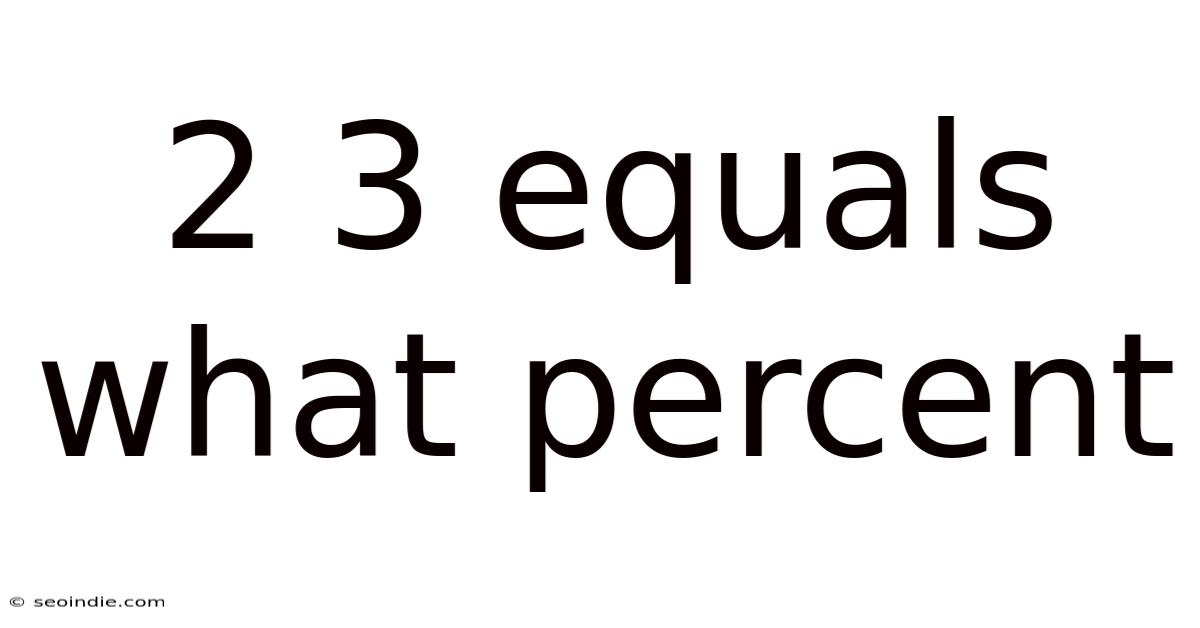
Table of Contents
2 is What Percent of 3? Understanding Percentages and Proportions
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This article delves into the question, "2 is what percent of 3?", providing a comprehensive explanation that goes beyond a simple answer. We'll explore the underlying mathematical principles, different calculation methods, and practical applications to solidify your understanding of percentages and proportions.
Introduction: Deconstructing the Problem
The question "2 is what percent of 3?" asks us to find the percentage that represents the ratio of 2 to 3. In essence, we're looking for the value 'x' in the equation: 2 = x% of 3. This seemingly simple question underpins a broader understanding of how percentages express parts of a whole. Mastering this concept unlocks the ability to solve various percentage-related problems, from calculating discounts to understanding statistical data.
Method 1: The Direct Percentage Calculation
The most straightforward way to determine what percent 2 is of 3 involves converting the ratio into a percentage. Here’s how:
-
Form the Ratio: Express the relationship between the two numbers as a fraction: 2/3.
-
Convert to Decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.6667
-
Convert to Percentage: Multiply the decimal by 100%: 0.6667 × 100% ≈ 66.67%
Therefore, 2 is approximately 66.67% of 3. The recurring decimal indicates that this percentage is an approximation. For many practical purposes, rounding to two decimal places (66.67%) provides sufficient accuracy.
Method 2: Using Proportions
Understanding proportions offers a more versatile approach to solving percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion to solve our problem:
-
Let x be the unknown percentage. We can write the proportion as:
2/3 = x/100 -
Cross-multiply: This means multiplying the numerator of one fraction by the denominator of the other and setting them equal. This gives us:
2 * 100 = 3 * x200 = 3x -
Solve for x: Divide both sides of the equation by 3:
x = 200/3x ≈ 66.67 -
Express as a percentage: Therefore, x ≈ 66.67%, confirming our previous result.
This method highlights the inherent relationship between ratios and percentages. It provides a flexible framework for solving a wider range of percentage-related problems.
Method 3: The Percentage Formula
A more generalized formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 2
- Whole: 3
Substituting these values into the formula:
(2/3) * 100% ≈ 66.67%
This formula emphasizes the fundamental concept of a percentage representing a part of a whole. It’s a powerful tool for a wide array of percentage calculations.
Understanding the Concept of Parts and Wholes
It's crucial to correctly identify the "part" and the "whole" in percentage problems. The "whole" is the total amount or the base value against which the "part" is compared. In our problem, 3 is the whole, and 2 is the part. Misidentifying these elements will lead to an incorrect result. For example, if we mistakenly considered 2 to be the whole and 3 to be the part, we would get a vastly different and incorrect answer.
Practical Applications: Real-World Examples
Understanding percentages is vital for various applications:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. For instance, a 66.67% discount on a $3 item means a reduction of approximately $2.
-
Data Analysis and Statistics: Percentages are used extensively to present and analyze data. For example, if 2 out of 3 students passed an exam, we can say that 66.67% of students passed.
-
Everyday Life: Understanding percentages helps us compare prices, make informed purchasing decisions, and understand proportions in various contexts.
Beyond the Basics: Dealing with More Complex Scenarios
The principles explained above can be extended to handle more complex percentage problems. Consider these examples:
-
Finding the Whole: If 20% of a number is 6, what is the number?
-
Finding the Part: What is 35% of 120?
-
Percentage Increase/Decrease: A value increased from 10 to 15; what is the percentage increase?
These problems require adapting the basic percentage formula and possibly using algebraic techniques to solve for the unknown variable.
Frequently Asked Questions (FAQ)
-
Q: Is 66.67% the exact answer?
- A: No, 66.67% is an approximation. The exact answer is a recurring decimal, 66.666...% The level of precision required depends on the context.
-
Q: What if I need more decimal places of accuracy?
- A: You can increase the number of decimal places in your calculator or software during the division step to achieve a higher level of accuracy.
-
Q: How can I practice solving percentage problems?
- A: There are numerous online resources, worksheets, and textbooks that offer practice problems with varying levels of difficulty. Working through these will reinforce your understanding.
-
Q: Are there any shortcuts for calculating percentages?
- A: While the methods described provide a solid foundation, some shortcuts exist for specific calculations. For instance, calculating 10% of a number simply involves moving the decimal point one place to the left. Understanding these shortcuts can speed up calculations, but a strong understanding of the underlying principles is always more important.
Conclusion: Mastering the Power of Percentages
The seemingly simple question, "2 is what percent of 3?" opens the door to a comprehensive understanding of percentages and proportions. By mastering the various calculation methods and underlying concepts, you equip yourself with a valuable skillset applicable in numerous fields. Remember the core principles: identifying the "part" and the "whole," utilizing proportions, and applying the fundamental percentage formula. Practice makes perfect; the more you work with percentages, the more intuitive and effortless they will become. From navigating financial transactions to interpreting data, understanding percentages is a key to success in many aspects of life.
Latest Posts
Latest Posts
-
Lcm Of 15 And 2
Sep 16, 2025
-
Lcm Of 12 And 21
Sep 16, 2025
-
Dna Replication Prokaryotes Vs Eukaryotes
Sep 16, 2025
-
Limits Of A Rational Function
Sep 16, 2025
-
Volume Rate Of Change Calculator
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Equals What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.