Y Varies Inversely With X
seoindie
Sep 14, 2025 · 6 min read
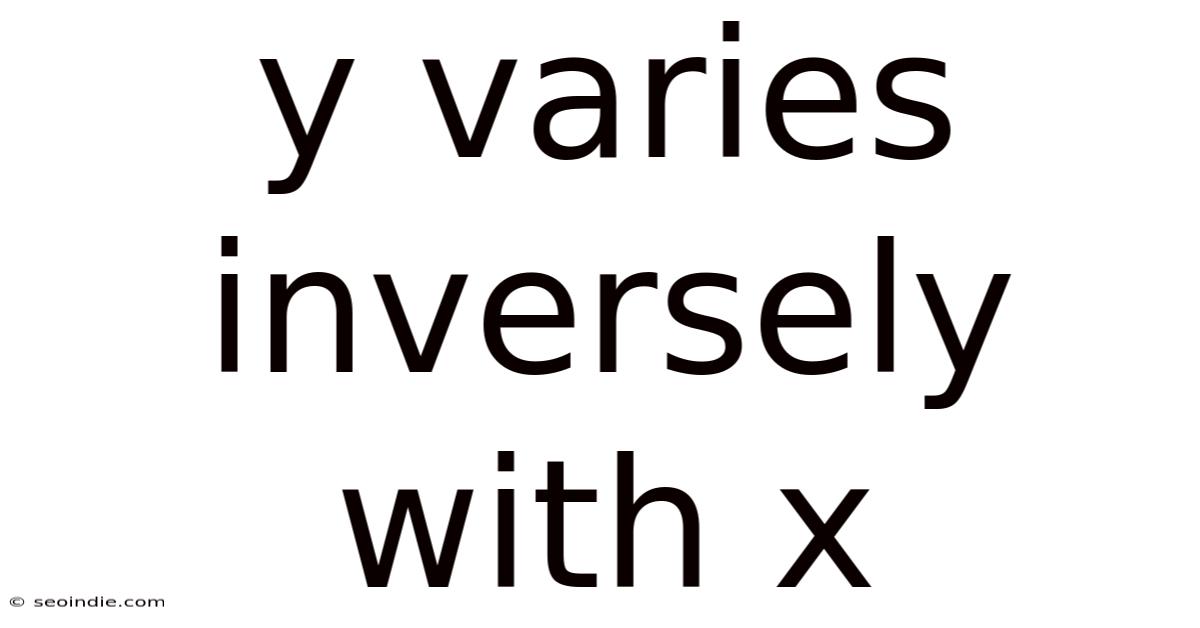
Table of Contents
Understanding Inverse Variation: When One Goes Up, the Other Goes Down
Inverse variation describes a relationship between two variables where an increase in one variable leads to a proportional decrease in the other, and vice versa. This concept is fundamental in mathematics and science, appearing in numerous applications from physics and engineering to economics and everyday life. This comprehensive guide will explore inverse variation in detail, covering its definition, representation, problem-solving techniques, and real-world examples. Understanding inverse variation is crucial for anyone studying algebra and beyond, providing a strong foundation for more advanced mathematical concepts.
Defining Inverse Variation
In its simplest form, we say that y varies inversely with x (or y is inversely proportional to x) if the product of x and y remains constant. This constant is often represented by the letter k, and is known as the constant of variation. Mathematically, we can express this relationship as:
y = k/x or xy = k
Where:
- y is the dependent variable
- x is the independent variable
- k is the constant of variation (k ≠ 0)
This equation tells us that as x increases, y decreases proportionally, and as x decreases, y increases proportionally. The graph of an inverse variation is a hyperbola, with the x and y axes as asymptotes. This means the graph approaches but never touches the axes.
Identifying Inverse Variation in Problems
Identifying whether a relationship is an inverse variation involves checking if the product of the two variables remains constant. Consider the following examples:
-
Example 1: If you travel a fixed distance, the time it takes to arrive is inversely proportional to your speed. A faster speed means less travel time, and a slower speed means more travel time. The product of speed and time is always equal to the total distance.
-
Example 2: The intensity of light from a source is inversely proportional to the square of the distance from the source. The further you are from the light, the dimmer it appears.
-
Example 3: The pressure of a gas is inversely proportional to its volume (at constant temperature), as stated by Boyle's Law. Increasing the volume of a gas decreases its pressure, and vice versa.
In each case, the product of the two variables is constant, indicating an inverse variation. If you're given a set of data points (x, y), check whether the product xy is consistent across all points. If it is, you have an inverse variation.
Solving Inverse Variation Problems
Solving problems involving inverse variation often requires finding the constant of variation (k) first. Once k is known, you can use the equation y = k/x to solve for either x or y, given the other variable.
Here's a step-by-step approach:
-
Identify the variables: Determine which variable varies inversely with the other.
-
Find the constant of variation (k): Use a given set of values for x and y to solve for k. Substitute these values into the equation xy = k.
-
Write the inverse variation equation: Substitute the value of k into the equation y = k/x.
-
Solve for the unknown variable: Use the equation from step 3 to find the value of either x or y, given the other variable.
Example:
If y varies inversely with x, and y = 6 when x = 2, find y when x = 3.
-
Variables: y varies inversely with x.
-
Find k: Using the given values, we have xy = k, so (2)(6) = k, therefore k = 12.
-
Equation: The inverse variation equation is y = 12/x.
-
Solve: When x = 3, y = 12/3 = 4. Therefore, y = 4 when x = 3.
Combined Variation: Incorporating Other Variables
Inverse variation can be combined with direct variation to create more complex relationships. For instance, a variable z might vary directly with x and inversely with y. This would be expressed as:
z = kx/y
Where k is the constant of variation. Solving problems with combined variation follows a similar approach to solving simple inverse variation problems, but requires careful consideration of the direct and inverse relationships between the variables.
Graphing Inverse Variation
The graph of an inverse variation, y = k/x, is a rectangular hyperbola. It has two branches, one in the first quadrant (where both x and y are positive) and one in the third quadrant (where both x and y are negative). The graph approaches but never touches the x-axis and y-axis, which are its asymptotes. The constant of variation, k, affects the shape of the hyperbola. A larger value of k results in a hyperbola further from the origin.
Real-World Applications of Inverse Variation
Inverse variation appears frequently in real-world scenarios. Some notable examples include:
-
Physics:
- Boyle's Law: As mentioned earlier, the pressure of a gas is inversely proportional to its volume at a constant temperature.
- Newton's Law of Universal Gravitation: The gravitational force between two objects is inversely proportional to the square of the distance between them.
- Ohm's Law: The current (I) flowing through a conductor is inversely proportional to its resistance (R) when the voltage (V) is constant (I = V/R).
-
Economics:
- Supply and Demand: Sometimes, the price of a good is inversely related to its supply. Higher supply may lead to lower prices, assuming other factors remain constant.
-
Everyday Life:
- Travel Time and Speed: The time it takes to travel a certain distance is inversely proportional to your speed.
- Gear Ratios in Bicycles: Higher gears result in faster speeds but require more effort, and lower gears allow for slower speeds but require less effort. This exemplifies an inverse relationship between speed and effort.
Frequently Asked Questions (FAQ)
Q: What is the difference between direct and inverse variation?
A: In direct variation, an increase in one variable leads to a proportional increase in the other (y = kx). In inverse variation, an increase in one variable leads to a proportional decrease in the other (y = k/x).
Q: Can the constant of variation (k) be zero?
A: No, the constant of variation cannot be zero. If k = 0, the equation y = k/x becomes y = 0/x = 0, which is not an inverse variation.
Q: What if the variables are inversely proportional to a power of the other variable, such as y = k/x²?
A: This represents an inverse square relationship. The principles remain the same, but the relationship is stronger. A small change in x will result in a larger change in y compared to a simple inverse relationship.
Q: How can I tell if a table of values represents an inverse variation?
A: Calculate the product of x and y for each data point. If the product is approximately constant for all data points, then it likely represents an inverse variation.
Conclusion
Understanding inverse variation is a crucial skill for anyone studying mathematics or related fields. This concept, while seemingly simple at first glance, underpins many important principles in physics, economics, and everyday life. By grasping the definition, representation, and problem-solving techniques associated with inverse variation, you'll gain a powerful tool for analyzing and interpreting relationships between variables. Remember to practice solving various problems to solidify your understanding. The more you work with inverse variation problems, the more intuitive and comfortable you'll become with this fundamental mathematical concept. From simple word problems to complex scientific applications, the ability to recognize and solve inverse variation problems will significantly enhance your mathematical abilities and analytical skills.
Latest Posts
Latest Posts
-
Objects That Begin With T
Sep 14, 2025
-
M M X I V
Sep 14, 2025
-
7 Times 7 Times 7
Sep 14, 2025
-
Algebra Equations That Equal 16
Sep 14, 2025
-
21 On The Periodic Table
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Y Varies Inversely With X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.