What Times What Equals 8
seoindie
Sep 19, 2025 · 6 min read
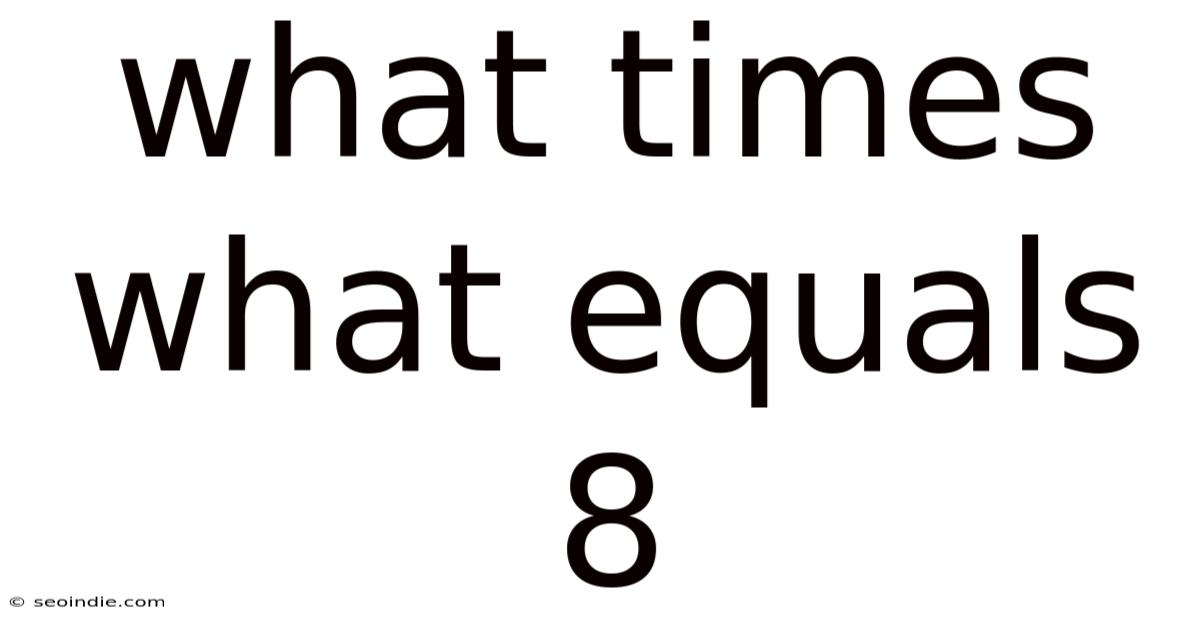
Table of Contents
What Times What Equals 8? Exploring the Factors and Applications of the Number 8
This article delves into the seemingly simple question: what times what equals 8? While the immediate answer might appear straightforward, exploring this question opens doors to broader mathematical concepts, including factors, multiplication, and the applications of number theory in various fields. We'll go beyond the basic solution and uncover the richness hidden within this fundamental arithmetic problem.
Introduction: Unveiling the Multiplicative Partners of 8
The number 8, a fascinating integer in itself, possesses a unique set of multiplicative partners. The most basic answer to "what times what equals 8?" is, of course, 2 x 4 = 8 and 4 x 2 = 8. However, this seemingly simple equation leads us down a path of exploration that reveals the deeper mathematical structures underpinning this seemingly simple question. Understanding the factors of 8 and how they interact provides a foundation for comprehending more advanced mathematical concepts. We will also touch upon the different ways this equation can be represented and its applications in various fields.
Finding the Factors: A Systematic Approach
The factors of a number are the whole numbers that divide it evenly without leaving a remainder. To find the factors of 8, we systematically search for pairs of numbers whose product equals 8:
- 1 x 8 = 8: This is the first and most obvious pair. 1 and 8 are both factors of 8.
- 2 x 4 = 8: Another pair revealing that 2 and 4 are also factors.
- 4 x 2 = 8: The commutative property of multiplication allows us to reverse the order.
- 8 x 1 = 8: Again, illustrating the commutative property.
Therefore, the factors of 8 are 1, 2, 4, and 8. These numbers, when multiplied together in various combinations, yield the number 8. This seemingly simple list forms the basis for understanding the multiplicative properties of 8 and its relationships with other numbers.
Beyond the Basics: Integer Solutions and Negative Numbers
Our initial exploration focused on positive integers. However, mathematics extends beyond this limited scope. Consider the possibility of negative numbers. Since the product of two negative numbers is positive, we can also find solutions involving negative numbers:
- (-1) x (-8) = 8: The product of two negative numbers results in a positive number.
- (-2) x (-4) = 8: Similarly, this pair also satisfies the equation.
- (-4) x (-2) = 8: Again, showcasing the commutative property.
- (-8) x (-1) = 8: Completing the set of negative factor pairs.
Including negative numbers significantly broadens the solutions to our initial question. It highlights the importance of considering the complete number system when solving mathematical problems.
Exploring Rational and Real Numbers: Expanding the Possibilities
The exploration doesn't end with integers. Let's consider rational numbers (fractions). Infinitely many pairs of rational numbers can multiply to 8. For example:
- (1/2) x 16 = 8
- (1/4) x 32 = 8
- (2/3) x 12 = 8
The possibilities here are endless. We can create infinite pairs by manipulating the numerator and denominator of the fractions. Similarly, real numbers (including irrational numbers like π) can also create infinitely many solutions. For example, we can choose a random real number x and then calculate 8/x to find its corresponding pair.
Visualizing the Solutions: A Geometric Perspective
The equation "what times what equals 8?" can also be visualized geometrically. Consider a rectangle with an area of 8 square units. The lengths of its sides represent the factors.
- A rectangle with sides of length 2 and 4 units has an area of 8 square units (2 x 4 = 8).
- A rectangle with sides of length 1 and 8 units also has an area of 8 square units (1 x 8 = 8).
This geometric representation offers an intuitive way to understand the factors of 8 and their relationship to area. This approach extends to other numbers and provides a visual bridge to connect abstract mathematical concepts with real-world applications.
The Prime Factorization of 8: A Fundamental Concept
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, etc.). The prime factorization of 8 is 2 x 2 x 2 = 2³. This means that 8 can be expressed as the product of three prime number 2s. Prime factorization is a fundamental concept in number theory and has significant applications in cryptography and other areas of mathematics.
Applications of the Number 8 and its Factors: Real-World Connections
The number 8 and its factors appear in various contexts:
- Geometry: The number 8 is frequently encountered in geometric shapes and calculations, such as the octagon (an eight-sided polygon).
- Music: Musical scales and rhythms often incorporate the number 8 and its multiples.
- Computer Science: Binary systems, fundamental to computing, use powers of 2, which directly relate to the number 8 (2³). Understanding powers of two is critical in memory management and data structures.
- Everyday Life: We encounter the number 8 in everyday scenarios like counting objects, dividing quantities, and scheduling tasks.
Frequently Asked Questions (FAQs)
-
Q: Are there any other ways to express 8 as a product of two numbers besides 2 x 4 and 1 x 8?
- A: No, if we are only considering whole numbers. However, as discussed earlier, if we include fractions, decimal numbers, or negative numbers, the possibilities become infinite.
-
Q: What is the importance of finding the factors of a number?
- A: Finding the factors of a number is crucial for various mathematical operations, including simplifying fractions, finding the greatest common divisor (GCD), and understanding divisibility rules. It is a fundamental step in various algebraic manipulations and number theory problems.
-
Q: Why is prime factorization important?
- A: Prime factorization is essential because it provides a unique representation for each number. This unique representation is fundamental in various mathematical fields, particularly number theory, cryptography, and computer science.
-
Q: Can the equation "what times what equals 8" be solved using only one number?
- A: No, multiplication inherently requires at least two numbers. However, we can represent 8 as a power of 2 (2³), but this is still a form of repeated multiplication.
Conclusion: A Deeper Understanding of Multiplication and Number Theory
The seemingly simple question, "what times what equals 8?", serves as a gateway to exploring fundamental mathematical concepts. From identifying factors and exploring negative numbers to understanding prime factorization and its applications, this seemingly basic equation reveals a surprising depth of mathematical richness. Through a combination of direct solutions, graphical representations, and exploration of different number systems, we’ve gained a comprehensive understanding not just of the specific equation but of broader mathematical principles. The journey from a simple multiplication problem to a deeper appreciation of number theory highlights the interconnectedness of mathematical concepts and their relevance to various aspects of our world.
Latest Posts
Latest Posts
-
V Words That Describe Someone
Sep 19, 2025
-
Mutually Exclusive Events Probability Examples
Sep 19, 2025
-
Spanish Words Beginning With E
Sep 19, 2025
-
Sound Waves Are Longitudinal Waves
Sep 19, 2025
-
Microscope Parts And Functions Pdf
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.