What Times What Equals 68
seoindie
Sep 17, 2025 · 5 min read
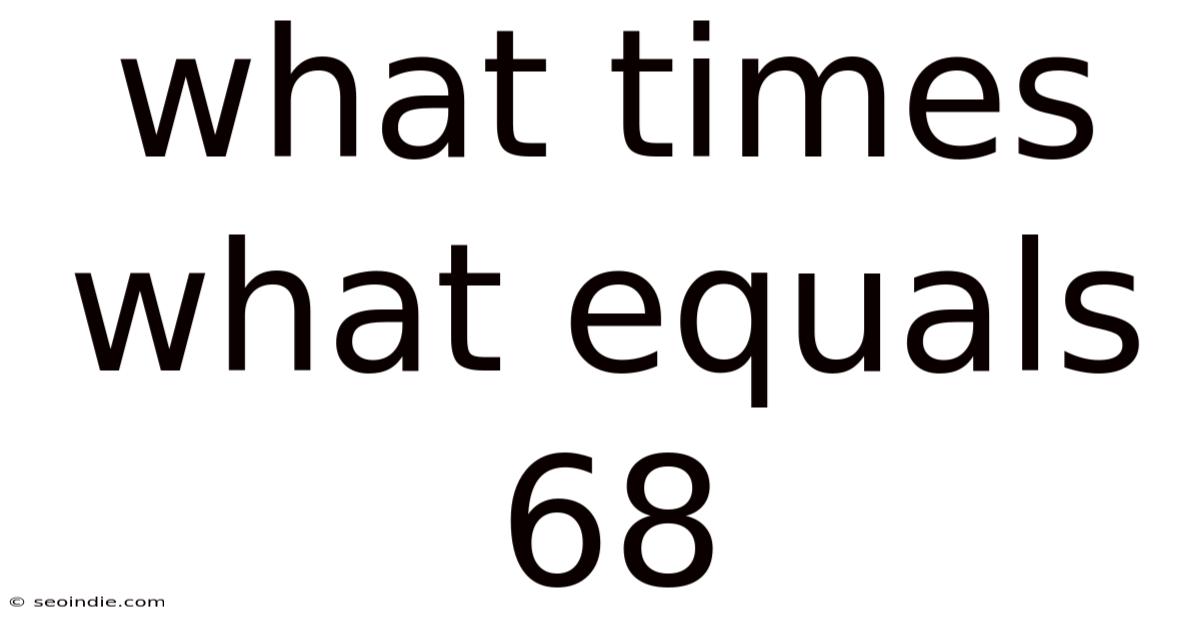
Table of Contents
What Times What Equals 68? Exploring Factors and Prime Factorization
Finding the pairs of numbers that multiply to equal 68 might seem like a simple arithmetic problem, but it opens the door to understanding fundamental concepts in mathematics, such as factors, prime numbers, and prime factorization. This seemingly straightforward question allows us to delve into the fascinating world of number theory and appreciate the elegance and logic inherent within. This comprehensive guide will not only answer the question "What times what equals 68?" but also provide a deeper understanding of the mathematical principles involved.
Understanding Factors
Before we dive into finding the pairs that multiply to 68, let's define what a factor is. Factors are whole numbers that divide evenly into another number without leaving a remainder. In simpler terms, if you can divide a number by a factor, the result will be a whole number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides evenly into 12.
Finding the Factor Pairs of 68
Now, let's tackle the main question: What times what equals 68? To find the pairs of numbers that multiply to 68, we need to find all the factors of 68. We can do this systematically:
- Start with 1: 1 x 68 = 68
- Check for 2: 2 x 34 = 68 (Since 68 is an even number, it's divisible by 2)
- Check for 3: 68 is not divisible by 3 (The sum of its digits, 6 + 8 = 14, is not divisible by 3).
- Check for 4: 4 x 17 = 68
- Check for 5: 68 is not divisible by 5 (It doesn't end in 0 or 5).
- Check for 6: 68 is not divisible by 6 (It's divisible by 2 but not by 3).
- Check for 7, 8, 9, 10... We continue checking until we reach a number larger than the square root of 68 (approximately 8.25). Once we surpass this point, we'll start repeating factor pairs we've already found.
Therefore, the factor pairs of 68 are:
- 1 x 68
- 2 x 34
- 4 x 17
These are all the possible pairs of whole numbers that, when multiplied, result in 68.
Prime Factorization: Breaking it Down Further
The concept of prime factorization helps us understand the fundamental building blocks of a number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. Prime factorization is the process of expressing a number as a product of its prime factors.
To find the prime factorization of 68, we can use a factor tree:
68
/ \
2 34
/ \
2 17
Following the branches of the tree, we see that 68 can be expressed as 2 x 2 x 17, or 2² x 17. This means that 2 and 17 are the prime factors of 68. This prime factorization is unique to 68; no other set of prime numbers will multiply to give 68. This uniqueness is a cornerstone of number theory.
Applying this Knowledge: Beyond 68
The principles we've explored with 68 can be applied to any whole number. Finding factors and performing prime factorization are fundamental skills in various mathematical areas, including:
- Algebra: Factoring expressions involves finding the factors of a polynomial, similar to finding the factors of a number.
- Calculus: Understanding factors is crucial in simplifying expressions and solving equations.
- Cryptography: Prime factorization plays a critical role in modern encryption methods. The difficulty of factoring large numbers into their prime components is the basis of many secure online transactions.
- Computer Science: Algorithms related to prime numbers and factorization are used in various computational tasks.
Expanding on the Concept: Finding Factors of Larger Numbers
While finding factors of smaller numbers like 68 is relatively straightforward, it becomes more challenging with larger numbers. For instance, let’s consider a much larger number, say 1729. Manually checking for factors would be tedious. Here are some strategies for finding factors of larger numbers:
- Divisibility Rules: Knowing divisibility rules for various numbers (e.g., a number is divisible by 3 if the sum of its digits is divisible by 3) can help quickly eliminate possibilities.
- Systematic Approach: Start checking divisibility by small prime numbers (2, 3, 5, 7, etc.) and systematically work your way up.
- Prime Factorization: Using prime factorization is often the most efficient method for larger numbers.
- Computational Tools: For extremely large numbers, computational tools and software can be used to quickly determine factors.
Frequently Asked Questions (FAQ)
Q: Are there any negative factors of 68?
A: Yes, there are. Since a negative number multiplied by a negative number results in a positive number, we can also consider the following pairs: -1 x -68, -2 x -34, and -4 x -17. These are all valid factor pairs.
Q: Is there only one prime factorization for a number?
A: Yes, the Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors).
Q: How can I improve my speed at finding factors?
A: Practice is key! Familiarize yourself with divisibility rules and try factoring various numbers. Using a systematic approach will also increase your efficiency.
Q: What are some real-world applications of finding factors?
A: Factors are crucial in many fields, including resource allocation (dividing resources evenly), scheduling (finding common multiples), and even in designing efficient computer algorithms.
Conclusion: Beyond the Simple Answer
The simple question "What times what equals 68?" has led us on a journey through the fascinating world of number theory. While the answer itself – 1 x 68, 2 x 34, and 4 x 17 – is straightforward, the underlying concepts of factors, prime numbers, and prime factorization are powerful tools with wide-ranging applications in mathematics and beyond. Understanding these concepts enhances our mathematical literacy and allows us to appreciate the elegance and logic inherent in the structure of numbers. By exploring this seemingly simple arithmetic problem, we've gained a deeper appreciation for the fundamental building blocks of mathematics. The next time you encounter a similar question, you'll be equipped not only to find the answer but also to understand the rich mathematical principles at play.
Latest Posts
Latest Posts
-
Words That Starts With At
Sep 18, 2025
-
5 Letter Words With O U
Sep 18, 2025
-
Can Electromagnets Repel Feromagnetic Metals
Sep 18, 2025
-
How Tall Is 40 Cm
Sep 18, 2025
-
Lcm Of 12 And 6
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 68 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.