What Times What Equals 38
seoindie
Sep 18, 2025 · 5 min read
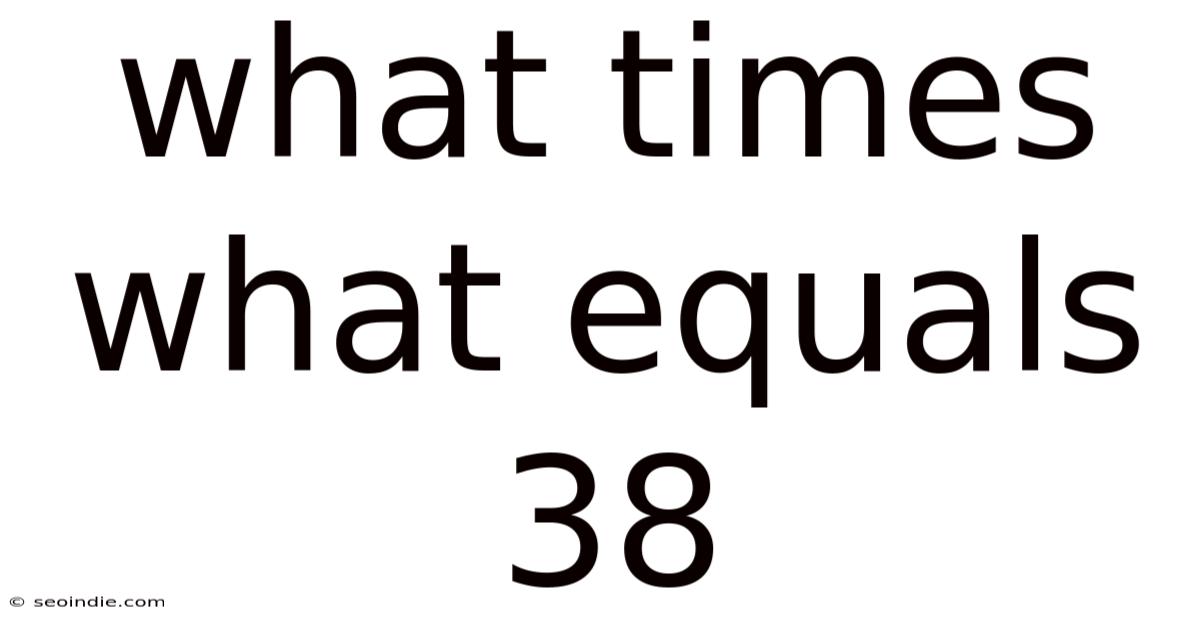
Table of Contents
What Times What Equals 38? Exploring Factor Pairs and Number Theory
Finding the numbers that, when multiplied, equal 38 might seem like a simple arithmetic problem. However, delving deeper reveals fascinating connections to number theory, prime factorization, and even more complex mathematical concepts. This article explores various approaches to solving "what times what equals 38," unraveling the seemingly straightforward question to uncover its underlying mathematical richness.
Introduction: Understanding Factor Pairs
The core of this problem lies in understanding factor pairs. A factor pair is a set of two numbers that, when multiplied together, produce a specific product. In this case, our product is 38. We're looking for all the pairs of numbers that, when multiplied, result in 38. This seemingly simple question opens doors to more complex mathematical ideas. Let's explore how to find these pairs systematically.
Methods for Finding Factor Pairs of 38
Several methods can be employed to identify the factor pairs of 38. Here are a few approaches, progressing from simple trial and error to more systematic techniques:
-
Trial and Error: The most straightforward approach is to start testing different pairs of numbers. We know that 1 is always a factor of any number, so we begin with (1, 38). Then we systematically check other pairs. Does 2 work? Yes, 2 x 19 = 38, giving us another factor pair (2, 19). Trying other numbers (3, 4, 5, etc.) reveals that there are no other whole number factors. This method is effective for smaller numbers but becomes cumbersome with larger numbers.
-
Prime Factorization: This more sophisticated method uses the concept of prime numbers – numbers divisible only by 1 and themselves. Prime factorization involves breaking down a number into its prime factors. Let's find the prime factorization of 38:
38 is an even number, so it's divisible by 2. 38 ÷ 2 = 19. 19 is a prime number. Therefore, the prime factorization of 38 is 2 x 19. This immediately reveals our factor pairs: (1, 38), (2, 19), (19, 2), and (38, 1). Note that the order of the pairs matters in this context. We are looking for the pairs of numbers that, when multiplied in this specific order, provide the result of 38.
-
Systematic Search: A systematic approach involves listing all possible divisors of 38. We start with 1 and check if it divides 38 evenly. It does (38 ÷ 1 = 38). Then we move to 2, which also divides 38 evenly (38 ÷ 2 = 19). Then we proceed with 3, 4, and so on. However, since 19 is a prime number, we've already found all the possible whole number factors. Therefore, we reach our factor pairs (1, 38) and (2, 19).
The Significance of Prime Factorization
The prime factorization method is particularly powerful because it provides a fundamental building block for understanding the number's properties. Knowing that 38 = 2 x 19 tells us much more than just its factor pairs. It reveals the irreducible components of the number. This is crucial in many areas of mathematics, including:
-
Greatest Common Divisor (GCD): Finding the greatest common divisor of two or more numbers is simplified using prime factorization. For instance, to find the GCD of 38 and another number, we can compare their prime factorizations.
-
Least Common Multiple (LCM): Similarly, finding the least common multiple uses prime factorization as a fundamental tool.
-
Modular Arithmetic: In modular arithmetic (working with remainders), prime factorization plays a vital role in understanding congruence relations and solving various problems.
-
Cryptography: Prime factorization is the foundation of many modern encryption algorithms. The difficulty of factoring large numbers into their prime components is what makes these systems secure.
Extending the Problem: Negative Factors and Rational Numbers
Our discussion so far has focused on positive whole numbers. However, we can extend the problem to include negative numbers and rational numbers (fractions).
-
Negative Factors: Since a negative number multiplied by a negative number produces a positive number, we can also consider the factor pairs (-1, -38) and (-2, -19). These pairs, when multiplied, also result in 38.
-
Rational Factors: If we allow rational numbers, the possibilities become infinite. For example, (1/2, 76), (4, 9.5), and countless other combinations would work.
Exploring Related Mathematical Concepts
The seemingly simple question, "What times what equals 38?" opens doors to several intriguing mathematical concepts:
-
Divisibility Rules: Understanding divisibility rules (rules that help determine if a number is divisible by another number without performing the division) can expedite finding factors. For example, the divisibility rule for 2 states that any even number is divisible by 2.
-
Number Theory: This branch of mathematics deals with the properties of integers. Prime numbers, factorization, and the concepts of GCD and LCM are all central to number theory.
-
Algebra: The question can be represented algebraically as x * y = 38, where x and y represent the unknown factors. Solving this equation would involve finding all possible pairs (x, y) that satisfy the equation.
Frequently Asked Questions (FAQ)
-
Q: Is there only one answer to "what times what equals 38"? A: No, there are several answers depending on whether you consider only positive whole numbers, negative numbers, or rational numbers. For positive whole numbers, there are two pairs: (1, 38) and (2, 19).
-
Q: How can I quickly find factors of larger numbers? A: Prime factorization is the most efficient method for larger numbers. However, for very large numbers, specialized algorithms are used in computer science.
-
Q: Why are prime numbers important in this context? A: Prime numbers are the building blocks of all other numbers. Understanding the prime factorization of a number provides fundamental insights into its properties.
Conclusion: Beyond the Simple Calculation
The seemingly simple question "What times what equals 38?" offers a gateway to a deeper understanding of number theory and its practical applications. From finding factor pairs through trial and error to employing the power of prime factorization, the exploration reveals the underlying mathematical structure and elegance. This journey demonstrates how a basic arithmetic problem can unveil rich mathematical concepts and connects seemingly simple calculations to broader mathematical principles used in advanced fields. The seemingly simple equation x * y = 38 serves as a microcosm of the beauty and intricacy found within the vast world of mathematics. It reminds us that even the most fundamental concepts can hold profound depth and significance.
Latest Posts
Latest Posts
-
Gcf Of 35 And 15
Sep 18, 2025
-
Is 87 Prime Or Composite
Sep 18, 2025
-
English Collective Nouns For Animals
Sep 18, 2025
-
Words With H And O
Sep 18, 2025
-
How Far Is 1 5 M
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.