What Times What Equals 35
seoindie
Sep 14, 2025 · 5 min read
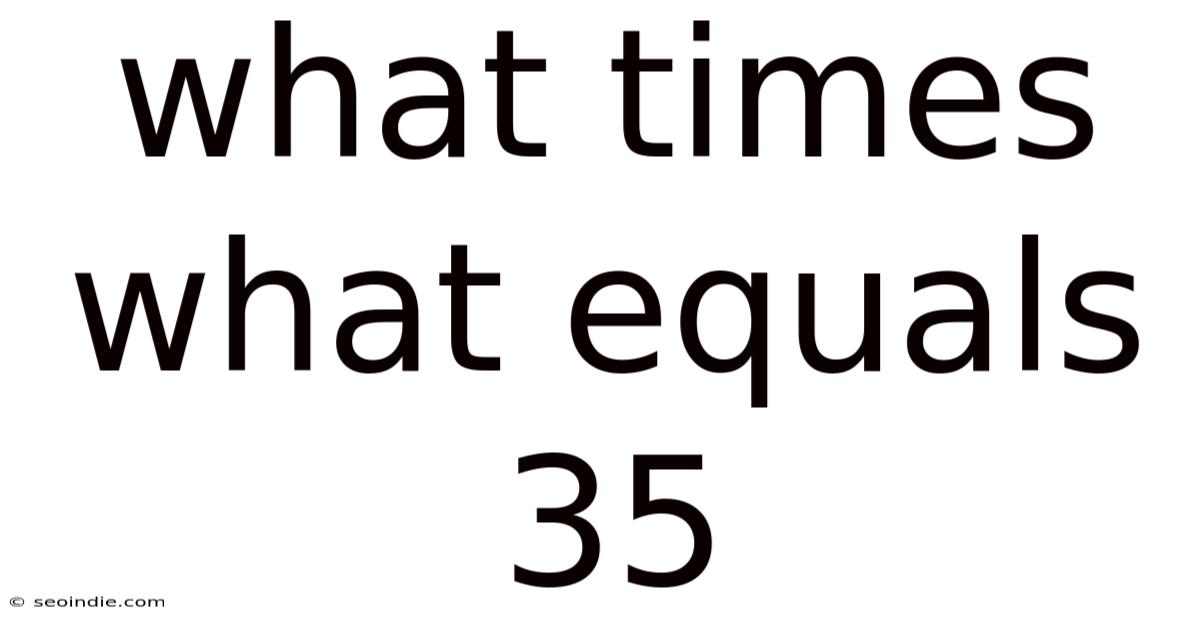
Table of Contents
What Times What Equals 35? Exploring Factor Pairs and Number Properties
Finding the numbers that, when multiplied, equal 35 might seem like a simple arithmetic problem. However, delving into this seemingly basic question opens doors to exploring fundamental concepts in mathematics, such as factor pairs, prime numbers, and the properties of multiplication. This article will not only answer the initial question but will also explore the broader mathematical context, providing a deeper understanding of number theory for students and anyone curious about the fascinating world of numbers.
Understanding Factor Pairs
The core of this problem lies in understanding factor pairs. A factor pair is a set of two numbers that, when multiplied together, produce a specific product. In this case, our product is 35. To find the factor pairs of 35, we need to identify all the pairs of numbers that multiply to give 35.
Let's start by systematically considering the numbers that divide evenly into 35:
- 1 and 35: 1 multiplied by 35 equals 35. This is one factor pair.
- 5 and 7: 5 multiplied by 7 equals 35. This is our second factor pair.
Therefore, the answer to "what times what equals 35?" is 1 x 35 and 5 x 7. These are all the possible integer factor pairs for the number 35.
Exploring Prime Numbers and Prime Factorization
The number 35 is a composite number, meaning it has more than two factors (1 and itself). However, its factor pairs include prime numbers. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, it's only divisible by 1 and itself.
In the factor pairs of 35, both 5 and 7 are prime numbers. This leads us to the concept of prime factorization. Prime factorization is the process of expressing a composite number as a product of its prime factors. For 35, the prime factorization is simply 5 x 7. This representation is unique for every composite number; there's only one way to express a number as a product of its prime factors.
Understanding prime factorization is crucial in various areas of mathematics, including simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM) of numbers. It also forms the basis for more advanced concepts in number theory and cryptography.
Extending the Problem: Negative Factors
So far, we've only considered positive integers. However, multiplication also involves negative numbers. Remember that multiplying two negative numbers results in a positive number. Therefore, we can also have negative factor pairs for 35:
- -1 and -35: -1 multiplied by -35 equals 35.
- -5 and -7: -5 multiplied by -7 equals 35.
This expands our understanding of the problem. The complete set of integer factor pairs for 35 includes both positive and negative pairs: (1, 35), (5, 7), (-1, -35), and (-5, -7).
Beyond Integers: Rational and Real Numbers
Our exploration can go even further. We've focused on integers, but the question "what times what equals 35?" can be answered using rational numbers (fractions) and even real numbers.
For example:
- 35/1 x 1: This is a trivial example, but it shows that we can use fractions.
- 7/2 x 10: (7/2) * 10 = 35. This illustrates the use of a fraction and an integer.
- √35 x √35: The square root of 35 multiplied by itself equals 35. This introduces real numbers into the equation.
The possibilities become almost endless when considering the entire set of real numbers.
Practical Applications: Real-World Scenarios
Understanding factor pairs and prime factorization isn't just an abstract mathematical exercise; it has practical applications in many areas:
- Geometry: Calculating the area of rectangles. If the area of a rectangle is 35 square units, the possible dimensions could be 1 unit by 35 units, or 5 units by 7 units.
- Algebra: Solving equations involving multiplication.
- Coding: Prime factorization is used in various algorithms and cryptographic systems.
- Everyday life: Dividing items or resources equally. For example, sharing 35 candies among friends.
Frequently Asked Questions (FAQ)
Q: Is 35 a prime number?
A: No, 35 is a composite number because it has more than two factors (1, 5, 7, and 35).
Q: What are the prime factors of 35?
A: The prime factors of 35 are 5 and 7.
Q: How do I find factor pairs for larger numbers?
A: For larger numbers, a systematic approach is helpful. Start by dividing the number by the smallest prime numbers (2, 3, 5, 7, and so on) to find its prime factors. Then, combine these factors to form all possible pairs. You can use factorization trees or other techniques to streamline the process.
Q: Are there any other ways to represent 35 as a product of numbers?
A: Yes, as discussed earlier, using fractions and irrational numbers opens up numerous possibilities beyond integer factor pairs.
Conclusion: Beyond the Simple Answer
While the initial answer to "what times what equals 35?" is straightforward (1 x 35 and 5 x 7, and their negative counterparts), this question serves as a gateway to exploring a wealth of mathematical concepts. Understanding factor pairs, prime numbers, prime factorization, and the broader implications of multiplication provides a solid foundation for further mathematical exploration. The seemingly simple problem of finding the factors of 35 touches upon core concepts that are fundamental to higher-level mathematics and numerous practical applications. By exploring this seemingly simple problem, we unveil the richness and interconnectedness within the world of numbers. Remember, even simple questions can lead to profound discoveries!
Latest Posts
Latest Posts
-
Number Of Protons Of Krypton
Sep 15, 2025
-
What Are The Representative Elements
Sep 15, 2025
-
How To Find Theoretical Mass
Sep 15, 2025
-
Biotic Factors In The Grasslands
Sep 15, 2025
-
Difference Between Homophones And Homonyms
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.