What Times What Equals 33
seoindie
Sep 20, 2025 · 5 min read
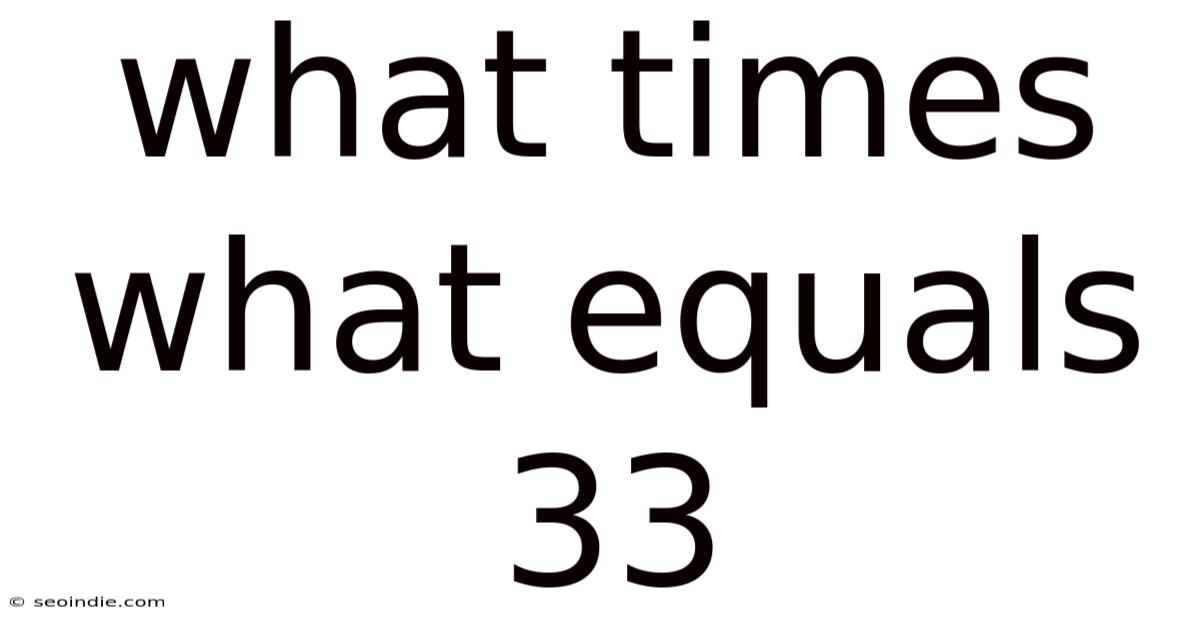
Table of Contents
What Times What Equals 33? Exploring Factor Pairs and Number Theory
Finding the numbers that multiply to equal 33 might seem like a simple arithmetic problem, but it opens a door to a deeper understanding of number theory, prime factorization, and even the intriguing world of algebra. This article will delve into the various ways to solve this seemingly simple equation, exploring different mathematical concepts along the way. We'll examine the straightforward solution, delve into the properties of factors, explore the concept of prime numbers, and even touch upon how this simple problem relates to more advanced mathematical ideas.
Understanding Factors and Factor Pairs
The core of this problem lies in understanding factors. Factors are numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. When we ask "what times what equals 33?", we're essentially searching for the factor pairs of 33. A factor pair consists of two numbers that, when multiplied together, result in the given number.
Let's find the factor pairs of 33. We can start by systematically checking each number:
- 1 x 33 = 33: This is the first obvious factor pair. One is always a factor of any number.
- 3 x 11 = 33: This is the second factor pair.
And that's it! 33 only has these two factor pairs, making it a relatively simple case. However, this simplicity highlights an important property of 33.
Prime Factorization: The Building Blocks of Numbers
The fact that 33 only has two factor pairs, excluding 1 and itself, makes it a composite number. A composite number is a positive integer that has at least one divisor other than 1 and itself. However, its constituent factors, 3 and 11, are both prime numbers.
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, its only divisors are 1 and itself. 3 and 11 both fit this definition. This leads us to the concept of prime factorization.
Prime factorization is the process of expressing a composite number as a product of its prime factors. For 33, the prime factorization is simply 3 x 11. This is a unique factorization; every composite number has only one prime factorization (ignoring the order of the factors). This fundamental theorem of arithmetic is a cornerstone of number theory.
Understanding prime factorization helps us to solve similar problems quickly. For example, if we were asked what numbers multiply to equal 77, we could immediately recognize that 77 = 7 x 11, both prime numbers, and hence 7 and 11 form the only factor pair (besides 1 and 77).
Expanding the Problem: Exploring Algebraic Approaches
Let's move beyond simple arithmetic and introduce some algebra. We can represent the problem "what times what equals 33" algebraically as:
x * y = 33
This equation has infinitely many solutions if we allow x and y to be any real number. For instance, x could be 1.5 and y would then be 22. However, if we restrict x and y to be integers (whole numbers), the solutions become limited to the factor pairs we've already identified: (1, 33), (3, 11), (11, 3), and (33, 1). The order matters here because we are looking for pairs.
We could add further constraints. For instance, if we stipulated that x must be less than y, then we would only have two solutions: (1, 33) and (3, 11). These constraints change the nature of the problem and demonstrate how seemingly simple questions can become more complex with the addition of conditions.
Beyond 33: Extending the Concept to Larger Numbers
The methods used to find the factors of 33 can be applied to any other number. However, as numbers get larger, the process becomes more involved. For example, finding the factors of a large number like 142857 might require a more systematic approach, such as using trial division or algorithms designed for factorization. Even then, factoring very large numbers is a computationally intensive task, crucial in cryptography where the difficulty of factoring large numbers is used to secure data.
Steps to Find Factors of Larger Numbers:
- Start with 1 and the number itself: These are always factors.
- Check for divisibility by small prime numbers: Test for divisibility by 2, 3, 5, 7, 11, and so on. Divisibility rules can be helpful here.
- Continue until you reach the square root of the number: If you haven't found any other factors by the time you reach the square root, you have found all the factors. Any remaining factor above the square root will have a corresponding factor below it that you've already found.
- List all factor pairs: Once you have found all the factors, pair them up to form the factor pairs.
Frequently Asked Questions (FAQ)
-
Q: Are there any negative factors of 33? A: Yes, (-1, -33) and (-3, -11) are also factor pairs because a negative number multiplied by a negative number results in a positive number.
-
Q: How many factors does 33 have? A: 33 has four factors: 1, 3, 11, and 33. Remember that we can include negative factors as well.
-
Q: What if the question was "what times what equals a negative number, like -33?" A: Then you'd need one positive and one negative factor. For example, 3 x -11 = -33, or -3 x 11 = -33.
-
Q: How do I find the factors of very large numbers efficiently? A: For very large numbers, specialized algorithms are necessary. These algorithms are beyond the scope of this article but are a fascinating area of study within number theory and computer science.
Conclusion: From Simple Arithmetic to Deeper Understanding
The seemingly simple question "What times what equals 33?" opens a gateway to explore fundamental concepts in number theory, such as factors, prime numbers, prime factorization, and algebraic representation. While the answer itself is straightforward (1 x 33 and 3 x 11), the journey of understanding how to arrive at this answer and the broader mathematical context it reveals is far more enriching. This exploration emphasizes that even seemingly basic arithmetic problems can lead to a deeper appreciation of the elegance and complexity of mathematics. The ability to break down problems, identify patterns, and connect them to underlying principles is a valuable skill applicable far beyond the realm of simple arithmetic.
Latest Posts
Latest Posts
-
Sodium Sulfate Anhydrous Molecular Weight
Sep 20, 2025
-
Circle Area Moment Of Inertia
Sep 20, 2025
-
English Words Ending With Ton
Sep 20, 2025
-
Gcf Of 3 And 9
Sep 20, 2025
-
20 Cm Converted To Inches
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.