What Times What Equals 31
seoindie
Sep 21, 2025 · 6 min read
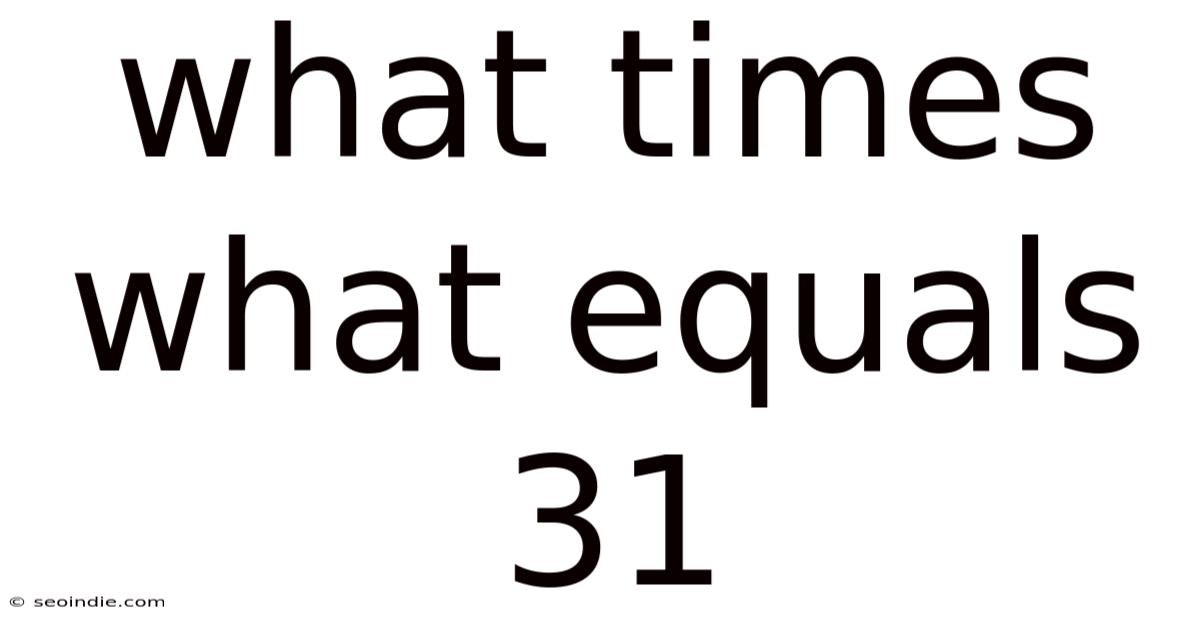
Table of Contents
What Times What Equals 31? Exploring Factor Pairs and Prime Numbers
Finding the answer to "What times what equals 31?" might seem simple at first glance. However, this seemingly straightforward question opens the door to a fascinating exploration of number theory, specifically focusing on factor pairs and the concept of prime numbers. This article will delve into the solution, explaining the mathematical concepts involved and expanding on their significance in broader mathematical contexts.
Understanding Factor Pairs
In mathematics, a factor pair consists of two numbers that, when multiplied together, produce a given number (in this case, 31). Identifying factor pairs is a fundamental skill in arithmetic and algebra, essential for simplifying expressions, solving equations, and understanding more complex mathematical concepts. For example, the factor pairs of 12 are (1, 12), (2, 6), (3, 4), and their reverses.
Solving for the Factors of 31
The question "What times what equals 31?" is essentially asking us to find the factor pairs of 31. Let's explore the possibilities:
- 1 x 31 = 31: This is the most obvious solution. 1 and 31 are a factor pair of 31.
- Are there any other whole number factors? Let's consider the factors between 1 and 31. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29—none of these numbers divide evenly into 31.
Therefore, the only whole number factor pairs for 31 are (1, 31) and (31, 1).
The Significance of Prime Numbers
This leads us to a crucial concept: prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. 31 fits this definition perfectly. It cannot be divided evenly by any whole number other than 1 and 31. This makes 31 a prime number.
Understanding prime numbers is fundamental to number theory. They are the building blocks of all other whole numbers, meaning that every whole number can be expressed as a unique product of prime numbers (this is known as the Fundamental Theorem of Arithmetic). This theorem underpins many areas of mathematics, including cryptography and computer science.
Exploring Further: Factors and Divisibility
Let's delve deeper into the concept of factors and divisibility rules. These rules help us quickly determine if a number is divisible by certain prime numbers without performing long division. While there isn't a specific divisibility rule for 31, understanding divisibility rules for other primes helps in the process of factorizing larger numbers:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 7: There is no simple rule for divisibility by 7, but various methods exist, often involving repeated subtraction or other algorithms.
- Divisibility by 11: A number is divisible by 11 if the alternating sum of its digits is divisible by 11.
These divisibility rules are useful for determining whether a number is divisible by these common prime factors before attempting to find factors for more complex numbers. They help streamline the factorization process.
Prime Factorization of Larger Numbers
Knowing the factors of a number, especially when dealing with prime numbers, is crucial for tasks such as finding the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. These concepts are frequently used in simplifying fractions, solving problems in algebra and number theory, and in applications like scheduling and resource allocation.
To illustrate this further, let's consider the number 62. We can find its prime factorization by systematically dividing by prime numbers:
- 62 is even, so it's divisible by 2: 62 = 2 x 31
- 31 is a prime number.
Therefore, the prime factorization of 62 is 2 x 31. Notice that 31, our original prime number, appears again in this factorization.
The Importance of Prime Numbers in Cryptography
The unique properties of prime numbers are extensively utilized in cryptography, the practice and study of techniques for secure communication in the presence of adversarial behavior. Many modern encryption algorithms rely on the difficulty of factoring very large numbers into their prime factors. The larger the number, and the more prime factors it has, the more computationally intensive it becomes to break the encryption. This computational complexity is what makes these cryptographic systems secure.
Expanding the Question: Beyond Whole Numbers
The initial question, "What times what equals 31?", was confined to whole numbers. However, we can expand the problem to include other number sets:
-
Rational Numbers: There are infinitely many pairs of rational numbers (fractions) that multiply to 31. For example, (2/3) * (93/2) = 31.
-
Real Numbers: Similarly, there's an infinite number of real number pairs that satisfy this equation.
-
Complex Numbers: The equation also has solutions within the set of complex numbers.
Frequently Asked Questions (FAQs)
-
Q: Is 31 the only prime number near that value? A: No. Other prime numbers near 31 include 29, 37, 41, 43, and so on. Prime numbers are scattered unevenly throughout the number line, with their distribution becoming less predictable as the numbers get larger.
-
Q: How can I find more prime numbers? A: There's no single, simple formula to generate all prime numbers. However, various methods and algorithms exist, including the Sieve of Eratosthenes, which is a systematic way to identify prime numbers up to a given limit. More advanced algorithms are used for finding larger prime numbers.
-
Q: Why are prime numbers important in cryptography? A: The difficulty of factoring large numbers into their prime components is the foundation of many modern cryptographic systems. The computational time required to factor a very large number into its prime factors makes it practically infeasible to break the encryption, ensuring data security.
Conclusion
The seemingly simple question, "What times what equals 31?", has led us on a journey through fundamental mathematical concepts like factor pairs and prime numbers. We've explored their significance in various mathematical branches and highlighted their crucial role in cryptography. Understanding these concepts is not only important for solving mathematical problems but also for appreciating the underlying structure and beauty of mathematics itself. While the immediate answer is 1 and 31, the deeper understanding gained through exploring this question is far more valuable. The exploration of this seemingly simple question demonstrates the depth and interconnectedness of mathematical concepts, offering a glimpse into the fascinating world of number theory.
Latest Posts
Latest Posts
-
Is Nitrogen A Pure Substance
Sep 21, 2025
-
4 Pics 7 Letter Words
Sep 21, 2025
-
What Is Volumetric Flow Rate
Sep 21, 2025
-
Find The Maclaurin Series Calculator
Sep 21, 2025
-
What Is 24 Square Root
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.