What Times What Equals 19
seoindie
Sep 24, 2025 · 4 min read
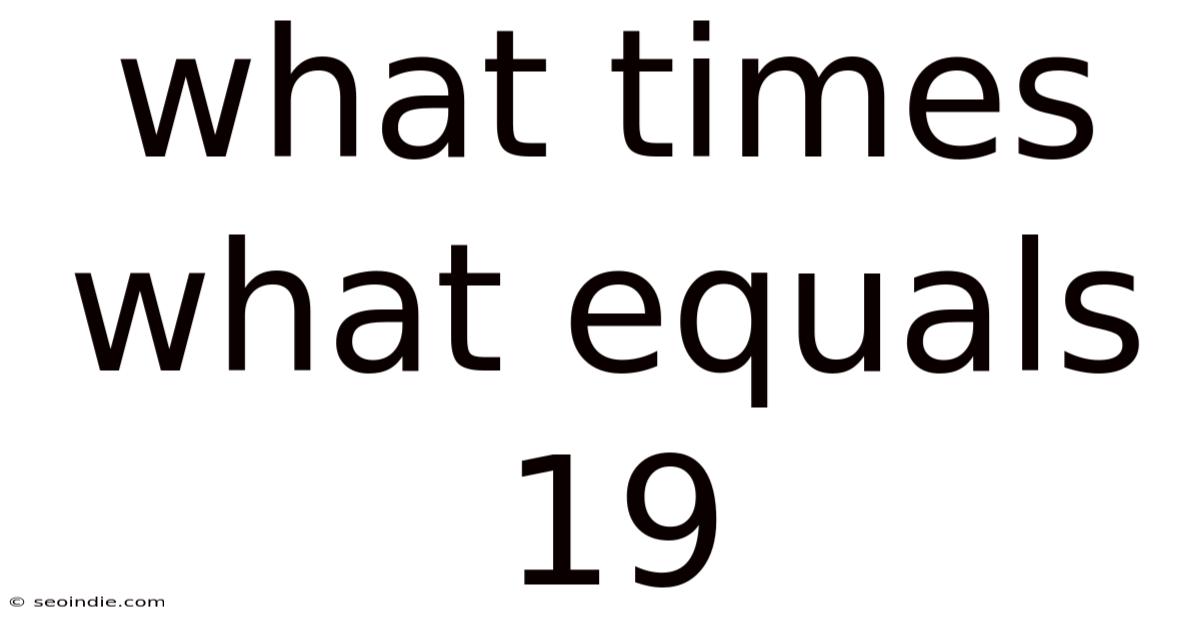
Table of Contents
What Times What Equals 19? Unpacking the Factors and Exploring Number Theory
Finding two whole numbers that multiply to equal 19 might seem like a simple task at first glance. However, delving into this seemingly basic question opens doors to a deeper understanding of number theory, prime numbers, and the fundamental building blocks of mathematics. This article will explore the solution, discuss its implications, and delve into related mathematical concepts.
Introduction: The Uniqueness of 19
The question, "What times what equals 19?" has a unique and straightforward answer within the realm of whole numbers: 1 x 19 = 19 and 19 x 1 = 19. This simplicity, however, belies the rich mathematical context surrounding the number 19. Understanding why these are the only whole number solutions requires understanding the concept of prime numbers.
Understanding Prime Numbers
A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime numbers are the fundamental building blocks of all other whole numbers, much like atoms are the building blocks of matter. They cannot be factored into smaller whole numbers other than 1 and themselves.
19 is a prime number. This means that it is only divisible by 1 and 19. This characteristic is crucial to understanding why there are only two solutions (1 x 19 and 19 x 1) to the equation x * y = 19, when considering only whole numbers.
Expanding the Search: Beyond Whole Numbers
If we expand our search beyond whole numbers and include rational numbers (fractions and decimals), the number of solutions becomes infinite. For example:
- 0.5 x 38 = 19
- 2 x 9.5 = 19
- 1/2 x 38 = 19
- 19/2 x 2 = 19
And so on. We can find an infinite number of pairs of rational numbers whose product is 19. This demonstrates the crucial difference between working within the constraints of whole numbers and venturing into the broader world of rational numbers.
The Significance of Prime Factorization
The prime factorization of a number is the unique representation of that number as a product of its prime factors. For example, the number 12 can be factored as 2 x 2 x 3 (or 2² x 3). This factorization is unique to 12. Every whole number (excluding 1) has a unique prime factorization. This is known as the Fundamental Theorem of Arithmetic.
Since 19 is a prime number, its prime factorization is simply 19. This inherent simplicity explains why the solution to "what times what equals 19" is so straightforward when restricted to whole numbers. The lack of other prime factors eliminates the possibility of multiple combinations of whole numbers resulting in a product of 19.
Exploring Related Concepts: Factors and Multiples
To fully appreciate the solution to our original question, let's explore related mathematical concepts:
-
Factors: Factors are numbers that divide evenly into a given number without leaving a remainder. For 19, the factors are 1 and 19.
-
Multiples: Multiples are the results of multiplying a number by whole numbers. The multiples of 19 are 19, 38, 57, 76, and so on.
Understanding the distinction between factors and multiples helps clarify why only 1 and 19 are the whole number solutions to our equation. They are the only numbers that, when multiplied, yield 19.
Thinking beyond the Equation: Applications in Real-World Scenarios
While the equation itself might seem abstract, the principles it illustrates have practical applications. The concept of prime factorization is fundamental to cryptography, particularly in securing online transactions. The unique factorization of numbers forms the basis of many encryption algorithms that protect sensitive data.
Frequently Asked Questions (FAQ)
-
Q: Are there any negative solutions to the equation?
- A: Yes, within the realm of integers (positive and negative whole numbers), we also have -1 x -19 = 19 and -19 x -1 = 19.
-
Q: How does this relate to algebra?
- A: This problem can be represented algebraically as xy = 19. Solving for x or y requires understanding factorization and the properties of prime numbers.
-
Q: What if we considered complex numbers?
- A: Extending the search to complex numbers introduces infinitely many more solutions, significantly increasing the complexity of the problem.
-
Q: Is 19 a special number?
- A: 19 is a prime number, and while prime numbers are infinitely many, each one holds a unique place in the number system's structure, contributing to the fundamental building blocks of mathematics.
Conclusion: The Beauty of Simplicity
The seemingly simple question, "What times what equals 19?", ultimately leads us on a journey into the fascinating world of number theory. Understanding prime numbers, factorization, and the properties of whole numbers allows us to appreciate not only the answer itself but also the underlying mathematical principles that govern it. The uniqueness of 19 as a prime number provides a clear and concise solution, highlighting the fundamental building blocks that make up the number system we use every day. This seemingly basic question helps illustrate the interconnectedness of concepts in mathematics and reveals the beauty of simplicity in a seemingly complex world. It serves as a gateway to further exploration of number theory and its applications across diverse fields. The beauty lies not only in the answer but in the journey of understanding it.
Latest Posts
Latest Posts
-
Words With I Second Letter
Sep 24, 2025
-
Job Description For A Dispatcher
Sep 24, 2025
-
One Third As A Percent
Sep 24, 2025
-
How Do We Measure Light
Sep 24, 2025
-
How Long Is 220 Minutes
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 19 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.