What Times What Equals 180
seoindie
Sep 12, 2025 · 6 min read
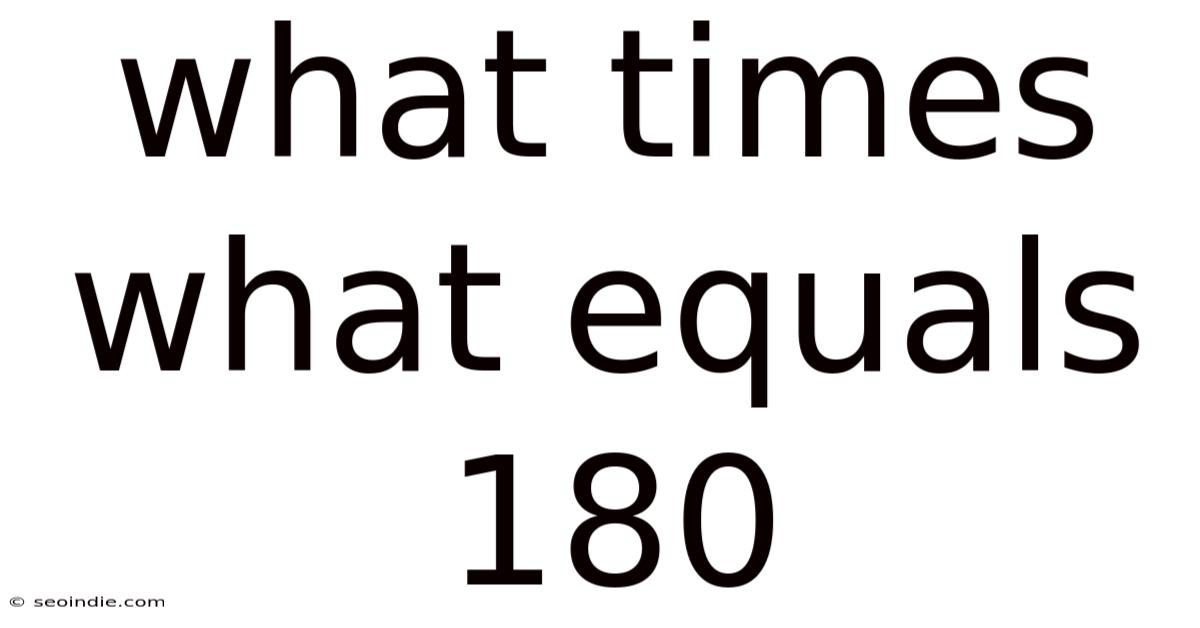
Table of Contents
What Times What Equals 180? Exploring the Factors and Applications of 180
Finding the numbers that multiply to equal 180 might seem like a simple arithmetic problem, but it opens the door to a deeper understanding of factors, prime factorization, and even more advanced mathematical concepts. This exploration will delve into the various pairs of numbers that produce 180, explain how to find them, and touch upon some of their practical applications. Understanding factor pairs is fundamental to many mathematical operations, from simplifying fractions to solving algebraic equations. Let's unravel the mystery of what times what equals 180.
Understanding Factors and Factor Pairs
Before we delve into the specifics of 180, let's establish a solid understanding of factors. Factors are whole numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides perfectly into 12.
A factor pair is a set of two factors that, when multiplied together, result in a specific number. For instance, (2, 6) and (3, 4) are factor pairs of 12 because 2 x 6 = 12 and 3 x 4 = 12. Finding all factor pairs of a number is a crucial step in many mathematical processes.
Finding the Factor Pairs of 180: A Step-by-Step Approach
There are several ways to systematically find all the factor pairs of 180. Let's explore a few approaches:
1. The Systematic Listing Method:
This method involves systematically listing all the factors and pairing them up. We start with the smallest factor, 1, and its corresponding pair:
- 1 x 180 = 180
- 2 x 90 = 180
- 3 x 60 = 180
- 4 x 45 = 180
- 5 x 36 = 180
- 6 x 30 = 180
- 9 x 20 = 180
- 10 x 18 = 180
- 12 x 15 = 180
This method is straightforward but can become time-consuming for larger numbers. Notice that we stopped at 12 because the next factor would be 15, and we've already paired 15 with 12.
2. Prime Factorization Method:
This method involves breaking down the number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). The prime factorization of 180 is:
180 = 2 x 2 x 3 x 3 x 5 = 2² x 3² x 5
Once you have the prime factorization, you can systematically combine these prime factors to find all the factor pairs. This method is especially useful for larger numbers. For example, using the prime factors of 180, we can create various combinations:
- (2, 90) – (2 x 1 x 3² x 5)
- (4, 45) – (2² x 1 x 3² x 5)
- (3, 60) – (1 x 3 x 2² x 3 x 5)
- (5, 36) – (1 x 5 x 2² x 3²)
- (6, 30) – (2 x 3 x 2 x 3 x 5)
- (9, 20) – (3² x 2² x 5)
- (10, 18) – (2 x 5 x 2 x 3²)
- (12, 15) – (2² x 3 x 3 x 5)
- (15, 12) – (3 x 5 x 2² x 3)
- (18, 10) – (2 x 3² x 2 x 5)
- (20, 9) – (2² x 5 x 3²)
- (30, 6) – (2 x 3 x 5 x 2 x 3)
- (36, 5) – (2² x 3² x 5)
- (45, 4) – (3² x 5 x 2²)
- (60, 3) – (2² x 3 x 5 x 3)
- (90, 2) – (2 x 3² x 5 x 2)
- (180, 1) – (2² x 3² x 5 x 1)
3. Using a Factor Tree:
A factor tree is a visual way to represent the prime factorization of a number. You start with the number 180 and repeatedly break it down into smaller factors until you reach only prime numbers.
180
/ \
2 90
/ \
2 45
/ \
3 15
/ \
3 5
From the factor tree, we obtain the prime factorization 2 x 2 x 3 x 3 x 5 (or 2² x 3² x 5), which can then be used to find the factor pairs as described above.
Beyond the Basics: Applications of Factor Pairs
Understanding factors and factor pairs extends far beyond basic arithmetic. Here are some examples:
-
Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator of a fraction requires finding the factors of both numbers. The GCF is then used to simplify the fraction to its lowest terms.
-
Solving Algebraic Equations: Factoring quadratic equations relies heavily on understanding factors. For example, solving the equation x² + 15x + 54 = 0 involves finding two numbers that add up to 15 and multiply to 54 (which are 6 and 9), allowing us to factor the equation as (x + 6)(x + 9) = 0.
-
Geometry and Area Calculations: When calculating the area of a rectangle, we multiply its length and width. If the area is known (e.g., 180 square units), finding the possible dimensions involves identifying factor pairs of 180.
-
Combinatorics and Probability: In combinatorial problems, finding the number of ways to arrange or select items often involves working with factorials (e.g., 5! = 5 x 4 x 3 x 2 x 1) and factors.
-
Number Theory: Many advanced topics in number theory, such as the study of perfect numbers and amicable numbers, are deeply rooted in the concept of factors and their properties.
Frequently Asked Questions (FAQs)
Q: What is the greatest common factor (GCF) of 180 and another number?
A: To find the GCF of 180 and another number, you would need to find the prime factorization of both numbers and identify the common prime factors raised to the lowest power. For example, if the other number is 240 (2⁴ x 3 x 5), the GCF of 180 and 240 would be 2² x 3 x 5 = 60.
Q: What are the divisors of 180?
A: The divisors of 180 are the same as its factors: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
Q: How many factors does 180 have?
A: 180 has 18 factors.
Q: Are there negative factor pairs for 180?
A: Yes, (-1, -180), (-2, -90), (-3, -60), and so on, are also valid factor pairs because a negative number multiplied by a negative number results in a positive number.
Conclusion: The Richness of Number Theory
The seemingly simple question, "What times what equals 180?" leads us on a journey through the fascinating world of factors, prime factorization, and their diverse applications across various mathematical fields. Understanding factors and factor pairs is not just about rote memorization; it's about developing a deeper intuition for numbers and their relationships, a skill that proves invaluable in more advanced mathematical explorations and problem-solving. This understanding forms the bedrock for more complex mathematical concepts and real-world applications. So, the next time you encounter a similar question, remember the systematic approaches and the underlying principles that unlock the secrets hidden within seemingly simple numbers.
Latest Posts
Latest Posts
-
Mutually Exclusive Events Are Independent
Sep 12, 2025
-
Is Inches Bigger Than Cm
Sep 12, 2025
-
How Do You Spell 56
Sep 12, 2025
-
How Many Lbs In 6kg
Sep 12, 2025
-
90 Square Meters In Feet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.