What Times What Equals 15
seoindie
Sep 14, 2025 · 6 min read
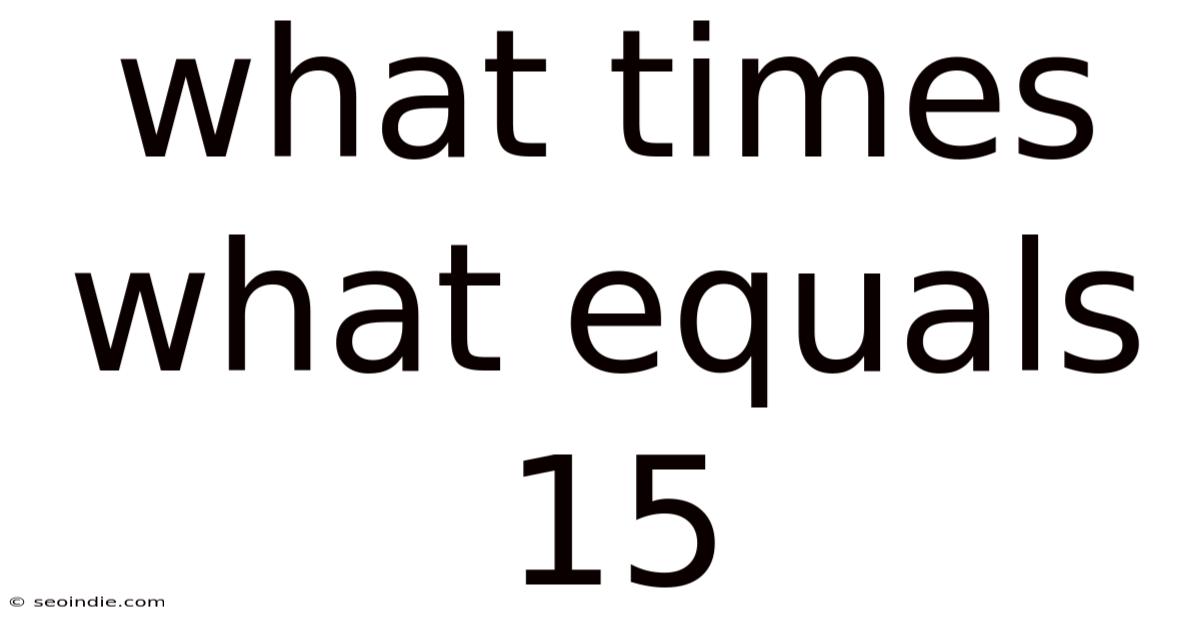
Table of Contents
What Times What Equals 15? Exploring the Factors and Applications of 15
Finding the factors of a number, such as discovering what numbers multiplied together equal 15, might seem like a simple arithmetic problem. However, understanding factor pairs opens doors to more advanced mathematical concepts and has practical applications in various fields. This article delves deep into the factors of 15, explores different mathematical approaches to finding them, and highlights their relevance in real-world scenarios. We'll move beyond the simple answer and uncover the underlying mathematical principles, making this seemingly basic question a gateway to deeper learning.
Introduction: Understanding Factors and Factor Pairs
In mathematics, a factor is a number that divides another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 evenly. A factor pair consists of two numbers that, when multiplied, result in a specific number. Therefore, the question "What times what equals 15?" is essentially asking for the factor pairs of 15.
Let's begin by directly addressing the question: The most obvious answer is 3 x 5 = 15. This is the prime factorization of 15, meaning it's expressed as a product of only prime numbers (numbers divisible only by 1 and themselves). However, there are other ways to arrive at 15 through multiplication, involving both positive and negative integers.
Finding the Factor Pairs of 15: Different Approaches
We can approach finding the factor pairs of 15 using several methods:
1. Listing Method: This is a straightforward approach, especially for smaller numbers like 15. We start by listing the whole numbers, starting from 1, and check which numbers divide 15 evenly:
- 1 divides 15 (15 ÷ 1 = 15)
- 3 divides 15 (15 ÷ 3 = 5)
- 5 divides 15 (15 ÷ 5 = 3)
- 15 divides 15 (15 ÷ 15 = 1)
This gives us the factor pairs: (1, 15), (3, 5), (5, 3), and (15, 1). Notice that (3,5) and (5,3) represent the same factor pair, just in a different order.
2. Prime Factorization: This method is particularly useful for larger numbers. We break down the number into its prime factors. The prime factorization of 15 is 3 x 5. This immediately tells us that 3 and 5 are the primary factors. From here, we can derive other factor pairs, including those with negative numbers: (-3, -5), (-5, -3), (-1, -15), and (-15, -1).
3. Systematic Search: For larger numbers, a systematic search might be necessary. We can start with 1 and progressively test each whole number until we find all factors. However, for a number as small as 15, this isn't as efficient as the listing method or prime factorization.
Expanding the Scope: Considering Negative Factors
The question "What times what equals 15?" doesn't explicitly restrict us to positive integers. Therefore, we must consider negative factors as well. Since a negative number multiplied by a negative number results in a positive number, we have additional factor pairs:
- (-1) x (-15) = 15
- (-3) x (-5) = 15
- (-5) x (-3) = 15
- (-15) x (-1) = 15
Including these negative factor pairs, we have a total of eight factor pairs for 15.
The Significance of Prime Factorization
The prime factorization of 15 (3 x 5) is crucial. Prime factorization is a fundamental concept in number theory and has wide-ranging applications:
-
Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator of a fraction relies on prime factorization. This allows us to simplify fractions to their lowest terms. For instance, simplifying 15/45 involves finding the GCF of 15 (3 x 5) and 45 (3 x 3 x 5), which is 15. Therefore, 15/45 simplifies to 1/3.
-
Solving Equations: In algebra, prime factorization is used to solve quadratic equations and other polynomial expressions. Factoring expressions allows us to find their roots or zeros.
-
Cryptography: Prime numbers play a critical role in cryptography, which is the study of secure communication. Many encryption algorithms rely on the difficulty of factoring very large numbers into their prime components.
-
Understanding Number Properties: Prime factorization helps us understand the properties of numbers, including their divisibility rules and relationships with other numbers.
Real-World Applications of Factors and Factor Pairs
While seemingly abstract, understanding factors and factor pairs has practical applications in everyday life:
-
Dividing Resources: Imagine you have 15 cookies and want to divide them equally among your friends. Knowing the factors of 15 (1, 3, 5, 15) allows you to determine how many friends you can share with and how many cookies each friend will receive.
-
Arranging Objects: Suppose you have 15 tiles and want to arrange them in a rectangular grid. The factor pairs of 15 (1x15, 3x5, 5x3, 15x1) give you several options for the dimensions of the rectangle.
-
Scheduling Tasks: If you need to complete a task in 15 minutes and want to break it down into smaller chunks, understanding the factors can help you schedule your time efficiently (e.g., three 5-minute intervals).
-
Geometry and Measurement: Factors play a role in calculating areas and volumes of shapes. For instance, finding the dimensions of a rectangle with an area of 15 square units involves finding the factor pairs of 15.
Frequently Asked Questions (FAQ)
Q: Are there any other numbers besides 3 and 5 that, when multiplied, equal 15?
A: No, 3 and 5 are the only prime numbers that multiply to 15. However, if we include negative integers and 1 and 15, we have the additional factor pairs mentioned earlier.
Q: What is the greatest common factor (GCF) of 15 and another number, say 20?
A: The prime factorization of 15 is 3 x 5, and the prime factorization of 20 is 2 x 2 x 5. The GCF is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 5. Therefore, the GCF of 15 and 20 is 5.
Q: How can I find the factors of larger numbers?
A: For larger numbers, prime factorization becomes increasingly important. You can use techniques like the division method or factor trees to break down the number into its prime factors. Once you have the prime factorization, you can systematically determine all the factor pairs.
Q: What is the least common multiple (LCM) of 15 and 20?
A: The LCM is the smallest number that is a multiple of both 15 and 20. To find it, we can use the prime factorizations. The prime factorization of 15 is 3 x 5, and for 20 it's 2 x 2 x 5. The LCM includes all prime factors raised to their highest powers: 2 x 2 x 3 x 5 = 60. Therefore, the LCM of 15 and 20 is 60.
Conclusion: Beyond a Simple Answer
The question "What times what equals 15?" seemingly has a simple answer: 3 x 5. However, by exploring the concept of factors, factor pairs, prime factorization, and their real-world applications, we've transformed this basic arithmetic problem into a gateway to a deeper understanding of number theory. This journey highlights the importance of looking beyond simple answers and exploring the underlying mathematical principles that govern seemingly simple numerical relationships. Understanding these concepts isn't just about solving mathematical problems; it's about developing a stronger foundation for future learning and problem-solving in various aspects of life. The simple question "What times what equals 15?" becomes a springboard to a much richer understanding of the world of numbers.
Latest Posts
Latest Posts
-
8 Cm Convert To Inches
Sep 14, 2025
-
All States And Capitals List
Sep 14, 2025
-
3000 Sq Ft To Meters
Sep 14, 2025
-
Is 81 A Composite Number
Sep 14, 2025
-
Sin 45 Degrees In Fraction
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.