What Times What Equal 96
seoindie
Sep 16, 2025 · 5 min read
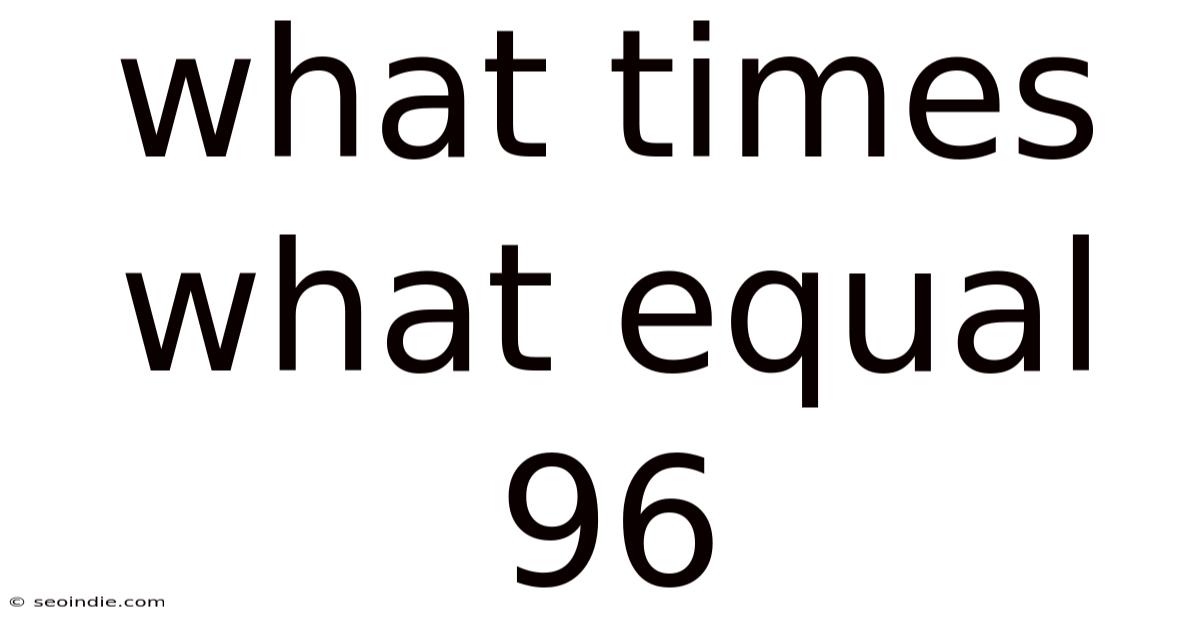
Table of Contents
What Times What Equals 96? Exploring the Factors and Applications of 96
Finding the numbers that multiply to equal 96 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental concepts in mathematics, including factors, prime factorization, and even applications in real-world scenarios. This comprehensive guide will not only provide you with all the possible pairs of numbers that multiply to 96 but also delve into the mathematical principles behind it, enriching your understanding of number theory.
Introduction: Understanding Factors and Multiplication
Before we dive into finding the pairs that equal 96, let's clarify what factors are. Factors are whole numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Our goal is to find all the pairs of factors that, when multiplied, result in 96.
Finding the Factor Pairs of 96: A Step-by-Step Approach
The most straightforward method is to systematically explore the numbers. We start by checking the smallest whole numbers and progress upwards:
-
1 x 96: This is the most obvious pair. Any number multiplied by 1 equals itself.
-
2 x 48: 96 is an even number, so it's divisible by 2.
-
3 x 32: 96 is divisible by 3 (9+6=15, and 15 is divisible by 3).
-
4 x 24: 96 is divisible by 4 (it's an even number divisible by 2 twice).
-
6 x 16: 96 is divisible by 6 (because it's divisible by both 2 and 3).
-
8 x 12: 96 is clearly divisible by 8 (8 x 12 = 96).
Now, notice something important. As we progress, we're approaching the square root of 96 (approximately 9.8). Once we pass this point, we start repeating factor pairs, just in reverse order. For example, we've already found 8 x 12; we won't find a new pair beyond 12.
Therefore, the complete list of factor pairs for 96 is:
- 1 x 96
- 2 x 48
- 3 x 32
- 4 x 24
- 6 x 16
- 8 x 12
Prime Factorization of 96: Breaking it Down to the Basics
Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). Prime factorization provides a unique representation of any number.
Let's find the prime factorization of 96:
-
Start with the smallest prime number, 2: 96 is even, so we can divide it by 2: 96 = 2 x 48
-
Continue dividing by 2: 48 is also even: 48 = 2 x 24; 24 = 2 x 12; 12 = 2 x 6; 6 = 2 x 3
-
We're left with a prime number, 3: The prime factorization is complete.
Therefore, the prime factorization of 96 is 2 x 2 x 2 x 2 x 2 x 3, which can be written as 2⁵ x 3. This prime factorization is unique to 96 and helps in various mathematical operations, including finding the greatest common divisor (GCD) and least common multiple (LCM) of numbers.
Mathematical Applications Beyond Simple Multiplication
The seemingly simple question, "What times what equals 96?", has far-reaching implications in various mathematical contexts:
-
Algebra: Finding factors is crucial in solving algebraic equations. For instance, factoring quadratic equations relies heavily on understanding factors.
-
Geometry: Factors appear in geometric problems involving areas and volumes. For example, if the area of a rectangle is 96 square units, you'd use factors to determine the possible dimensions of the rectangle.
-
Number Theory: The study of numbers and their properties extensively uses concepts like prime factorization and divisors, which are directly related to finding factors.
-
Combinatorics and Probability: Determining the number of possible combinations or arrangements often involves finding factors and using prime factorization to simplify calculations.
Real-World Applications: Beyond the Classroom
The concept of factors extends beyond theoretical mathematics and finds practical applications in many real-world situations:
-
Dividing Resources: Imagine you have 96 candies and want to divide them equally among a group of people. Understanding the factors of 96 will tell you all the possible group sizes you can have without any candies left over.
-
Arranging Objects: Suppose you need to arrange 96 chairs in a rectangular formation for an event. Knowing the factors helps determine the possible dimensions of the rectangular arrangement.
-
Scheduling and Planning: In project management or event planning, dividing tasks or time slots often involves finding factors to ensure efficient resource allocation.
Frequently Asked Questions (FAQs)
-
Are there negative factor pairs for 96? Yes, there are. Since a negative number multiplied by a negative number results in a positive number, you could also have pairs like -1 x -96, -2 x -48, and so on.
-
How do I find factors quickly for larger numbers? For larger numbers, prime factorization is a more efficient method. Once you have the prime factorization, you can easily combine the prime factors in different ways to find all possible factor pairs.
-
What is the significance of prime factorization? Prime factorization provides a unique representation of a number, which is fundamental in various mathematical operations and applications. It simplifies calculations and helps understand the structure of numbers.
-
What if I need to find factors for a very large number? For extremely large numbers, specialized algorithms and computer programs are used to find their prime factorization efficiently.
Conclusion: More Than Just a Math Problem
The seemingly simple question of "What times what equals 96?" opens a window into a rich world of mathematical concepts and their applications. By understanding factors, prime factorization, and their relevance in various mathematical fields and real-world scenarios, we gain a deeper appreciation for the fundamental building blocks of numbers and their powerful role in problem-solving. This seemingly simple arithmetic exercise showcases the interconnectedness of various mathematical concepts and their relevance in everyday life, highlighting the beauty and practicality of mathematical understanding. So, the next time you encounter a similar question, remember that it's not just about finding the answer; it's about understanding the underlying principles and their broader implications.
Latest Posts
Latest Posts
-
Area Of Triangle Using Matrix
Sep 16, 2025
-
Convert 36 Inches To Cm
Sep 16, 2025
-
What Are Factors Of 200
Sep 16, 2025
-
Arrhenius Definition Of An Acid
Sep 16, 2025
-
Is Ncert Enough For Neet
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equal 96 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.