What Times What Equal 54
seoindie
Sep 20, 2025 · 6 min read
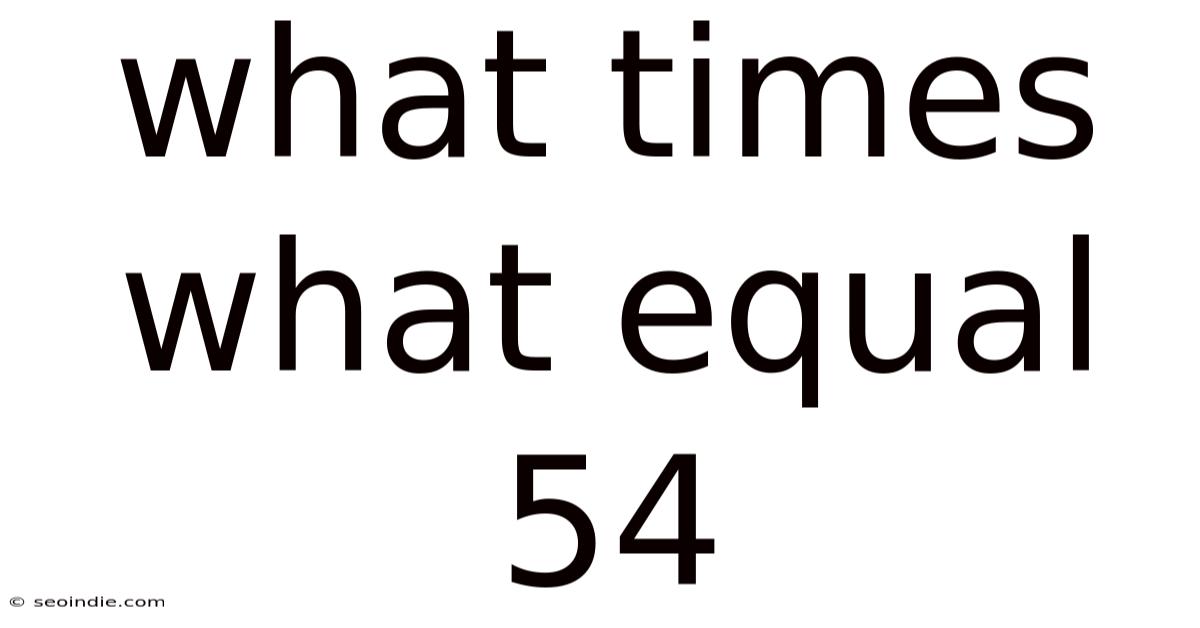
Table of Contents
Decoding the Mystery: What Times What Equals 54? A Deep Dive into Factor Pairs and Number Theory
Finding the numbers that, when multiplied, result in 54 might seem like a simple arithmetic problem. However, this seemingly straightforward question opens a door to a fascinating world of number theory, exploring concepts like factors, prime factorization, and even the relationship between multiplication and division. This comprehensive guide will not only provide you with the answers but will also equip you with a deeper understanding of the underlying mathematical principles.
Understanding Factors and Factor Pairs
Before diving into the specific problem of "what times what equals 54," let's establish a firm understanding of fundamental concepts. A factor of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. A factor pair consists of two factors that, when multiplied, produce the original number. For 12, the factor pairs are (1, 12), (2, 6), and (3, 4).
Finding the factor pairs of a number is crucial to solving problems like "what times what equals 54?" It involves systematically exploring different combinations of whole numbers to identify those that result in the target number (54 in this case).
Finding the Factor Pairs of 54: A Step-by-Step Approach
Now, let's tackle the core question: What times what equals 54? We can approach this systematically:
-
Start with 1: Since 1 is a factor of every number, we know that 1 multiplied by 54 equals 54. Our first factor pair is (1, 54).
-
Check for divisibility by 2: 54 is an even number, so it's divisible by 2. 54 divided by 2 is 27. This gives us the factor pair (2, 27).
-
Check for divisibility by 3: The sum of the digits of 54 (5 + 4 = 9) is divisible by 3, indicating that 54 itself is divisible by 3. 54 divided by 3 is 18. This yields the factor pair (3, 18).
-
Check for divisibility by 4: 54 is not divisible by 4.
-
Check for divisibility by 5: 54 is not divisible by 5 (numbers divisible by 5 end in 0 or 5).
-
Check for divisibility by 6: We already know 54 is divisible by 2 and 3, so it must be divisible by 6 (since 2 x 3 = 6). 54 divided by 6 is 9. This gives us the factor pair (6, 9).
-
Check for divisibility by 7: 54 is not divisible by 7.
-
Check for divisibility by 8: 54 is not divisible by 8.
-
Check for divisibility by 9: We already found that 54 is divisible by 9 (step 6).
-
Check for divisibility by higher numbers: We've now reached a point where checking higher numbers becomes redundant. The next factor would be higher than the factors we've already identified. We've systematically covered all the possibilities.
Therefore, the factor pairs of 54 are: (1, 54), (2, 27), (3, 18), and (6, 9). These are all the possible combinations of two whole numbers that multiply to equal 54.
Prime Factorization: A Deeper Look
The concept of prime factorization provides a more fundamental understanding of the factors of a number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11...). Prime factorization involves expressing a number as a product of its prime factors.
To find the prime factorization of 54:
- We start by dividing 54 by the smallest prime number, 2: 54 ÷ 2 = 27.
- 27 is not divisible by 2, but it is divisible by 3: 27 ÷ 3 = 9.
- 9 is also divisible by 3: 9 ÷ 3 = 3.
- 3 is a prime number.
Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3, or 2 x 3³. This representation shows the building blocks of 54 as prime numbers. Understanding prime factorization provides a powerful tool for analyzing numbers and their factors.
Applications Beyond Simple Multiplication
The seemingly simple question of "what times what equals 54" extends far beyond basic arithmetic. Understanding factor pairs and prime factorization is fundamental in various mathematical fields, including:
-
Algebra: Solving quadratic equations often involves factoring expressions, a process that directly utilizes the understanding of factor pairs.
-
Number Theory: Advanced number theory explores properties of numbers, including factors, prime numbers, and their relationships. Concepts like the greatest common divisor (GCD) and the least common multiple (LCM) rely heavily on factorization techniques.
-
Cryptography: Modern encryption methods utilize prime numbers and their properties to secure digital information. The difficulty of factoring extremely large numbers into their prime factors forms the basis of many cryptographic algorithms.
-
Computer Science: Algorithms related to number theory, such as finding prime numbers efficiently, have significant applications in computer science and software development.
Frequently Asked Questions (FAQ)
Q: Are there any negative factors of 54?
A: Yes, if we consider negative integers, we can also have factor pairs like (-1, -54), (-2, -27), (-3, -18), and (-6, -9). When multiplying two negative numbers, the result is positive.
Q: Is there only one way to express 54 as a product of numbers?
A: No, while the prime factorization is unique (except for the order of factors), there are multiple ways to express 54 as a product of its factors. For example, 54 can also be expressed as 2 x 27, 3 x 18, or 6 x 9.
Q: How can I find the factors of larger numbers?
A: For larger numbers, systematic approaches like checking for divisibility by prime numbers, or using factorization algorithms, are more efficient. Software and online tools can also assist with finding factors of very large numbers.
Q: What is the significance of prime factorization?
A: Prime factorization is fundamental in number theory because it provides a unique representation of any positive integer greater than 1. This unique representation simplifies the study of many number-theoretic properties and is essential in several advanced mathematical and computational applications.
Conclusion: More Than Just a Simple Question
The question "what times what equals 54" might initially seem trivial. However, a deeper exploration reveals that it’s a gateway to a wealth of mathematical concepts. Understanding factors, factor pairs, and prime factorization isn't just about performing simple calculations; it's about developing a fundamental understanding of number theory and its far-reaching applications in various fields. By mastering these concepts, you unlock a more profound appreciation for the intricate beauty and underlying structure of numbers. This understanding will serve as a strong foundation for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
How Do You Spell 2
Sep 20, 2025
-
100 Acres To Sq Miles
Sep 20, 2025
-
Is Dirt Abiotic Or Biotic
Sep 20, 2025
-
How To Describe Childrens Personality
Sep 20, 2025
-
What Is 90 Divisible By
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equal 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.