What Times 1.5 Is 70
seoindie
Sep 18, 2025 · 5 min read
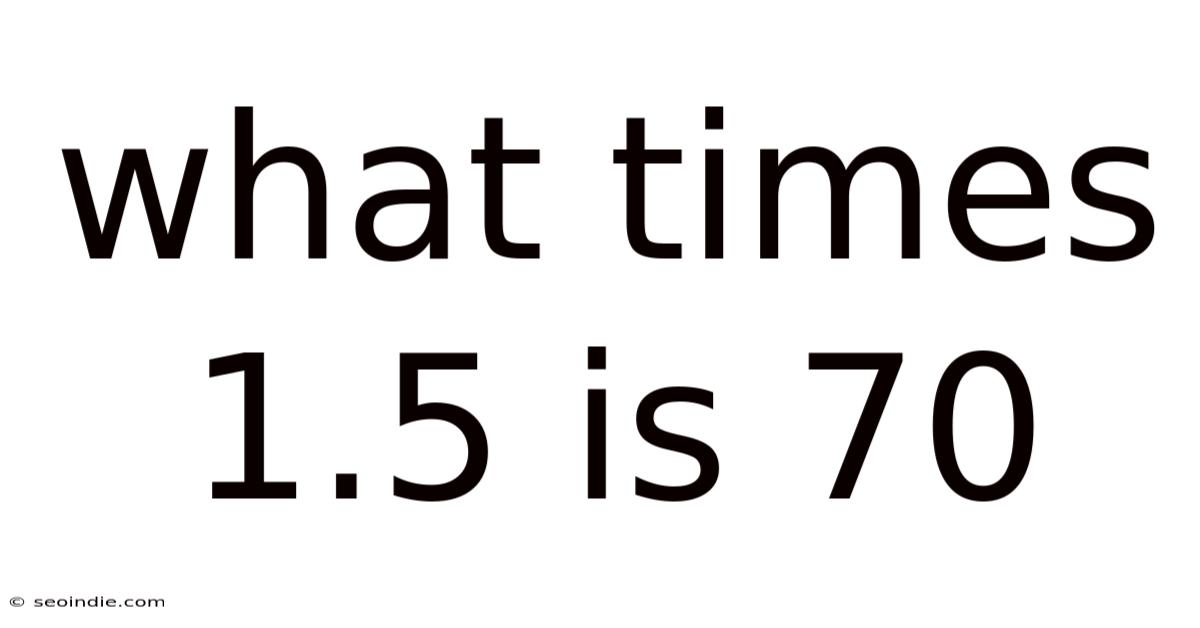
Table of Contents
What Times 1.5 is 70? Unlocking the Power of Algebra
Finding the unknown number that, when multiplied by 1.5, equals 70 is a common problem encountered in basic algebra. This seemingly simple question touches upon fundamental mathematical concepts and problem-solving strategies applicable across various fields. This article will not only solve this specific problem but also delve into the underlying principles, offering a comprehensive understanding for learners of all levels. We will explore different methods to arrive at the solution, discuss the significance of algebraic thinking, and address potential FAQs.
Understanding the Problem: Deconstructing "What Times 1.5 is 70?"
The core of the problem lies in identifying the unknown variable. We can represent this unknown number with a variable, typically 'x'. The question, "What times 1.5 is 70?", translates directly into an algebraic equation:
1.5x = 70
Our goal is to isolate 'x' on one side of the equation to find its value. This process involves applying inverse operations to maintain the equation's balance.
Method 1: Using Inverse Operations (Division)
The most straightforward approach involves using the inverse operation of multiplication, which is division. Since 'x' is multiplied by 1.5, we divide both sides of the equation by 1.5:
1.5x / 1.5 = 70 / 1.5
This simplifies to:
x = 70 / 1.5
Now, we perform the division:
x ≈ 46.67
Therefore, the number that, when multiplied by 1.5, is approximately 70 is 46.67. The slight discrepancy from an exact whole number arises due to the decimal nature of 1.5.
Method 2: Converting to Fractions for Easier Calculation
Working with decimals can sometimes be cumbersome. We can convert 1.5 into a fraction to simplify the calculation. 1.5 is equivalent to 3/2. Our equation now becomes:
(3/2)x = 70
To isolate 'x', we multiply both sides by the reciprocal of 3/2, which is 2/3:
(2/3) * (3/2)x = 70 * (2/3)
This simplifies to:
x = 140/3
Converting this fraction to a decimal:
x ≈ 46.67
This method yields the same result as the previous one, confirming our answer. Using fractions can be beneficial for understanding the underlying mathematical principles and may be easier for some individuals to calculate.
Method 3: Using a Calculator
For practical purposes, particularly when dealing with more complex numbers, a calculator provides a quick and efficient solution. Simply input "70 ÷ 1.5" into your calculator to obtain the answer, 46.67. While this method is convenient, it's crucial to understand the underlying mathematical principles to solve similar problems without relying solely on a calculator.
The Significance of Algebraic Thinking
Solving "What times 1.5 is 70?" is more than just finding a numerical answer. It demonstrates the power of algebraic thinking: the ability to represent unknown quantities with variables and manipulate equations to find solutions. This skill is fundamental to:
- Problem-solving in various fields: From engineering and physics to finance and computer science, the ability to model real-world problems using algebraic equations is indispensable.
- Developing critical thinking skills: Algebra encourages logical reasoning and the ability to break down complex problems into smaller, manageable steps.
- Improving mathematical proficiency: A strong grasp of algebraic concepts builds a solid foundation for advanced mathematical studies.
Extending the Concept: Variations and Applications
The core principle of solving for an unknown variable by using inverse operations remains consistent across a wide range of problems. Consider these variations:
- What times 2.5 is 100? This problem follows the same structure; we would set up the equation 2.5x = 100 and solve for x.
- What number, when multiplied by 0.75, equals 60? Here, the equation would be 0.75x = 60.
- If 1.5 times a certain quantity is 70, what is 2 times that quantity? This problem requires solving for the initial quantity (as we've already done) and then multiplying it by 2.
These variations emphasize the versatility of the algebraic approach. The same principles apply, even when the numbers or the context changes.
Real-world Applications
The ability to solve equations like "What times 1.5 is 70?" has numerous real-world applications:
- Scaling recipes: If a recipe calls for 1.5 cups of flour and you want to make a larger batch that requires 70 cups of flour, you can use this method to determine the scaling factor.
- Calculating unit costs: If 1.5 kilograms of a product costs $70, you can use this method to find the cost per kilogram.
- Determining proportions: Many engineering, scientific, and business problems involve determining proportions or scaling factors, and solving equations like this is essential.
- Financial calculations: Interest calculations, loan repayments, and investment returns often involve solving similar algebraic equations.
Frequently Asked Questions (FAQs)
Q: Is there only one way to solve this problem?
A: No, there are multiple approaches, as demonstrated in the different methods outlined above. The best approach often depends on personal preference and the complexity of the numbers involved.
Q: What if the equation were more complex, involving multiple variables or operations?
A: More complex equations require a systematic approach, often involving combining like terms, applying the order of operations (PEMDAS/BODMAS), and potentially utilizing more advanced algebraic techniques.
Q: Why is it important to understand the underlying principles rather than just using a calculator?
A: While calculators are convenient for quick calculations, understanding the underlying mathematical principles allows you to tackle more complex problems, adapt to different situations, and develop critical thinking skills.
Q: Can I use this approach for other mathematical problems?
A: Absolutely! The fundamental principles of algebra – isolating variables using inverse operations – are applicable to a vast range of mathematical problems beyond this specific example.
Conclusion: Mastering the Fundamentals
Solving "What times 1.5 is 70?" might appear simple at first glance. However, delving into the solution reveals a wealth of underlying mathematical concepts and problem-solving strategies. This seemingly straightforward question provides a foundational stepping stone to understanding the power of algebra, a crucial skill applicable across numerous disciplines. By mastering these fundamentals, learners equip themselves with valuable tools for tackling more complex challenges and fostering a deeper appreciation for the beauty and utility of mathematics. Remember, the ability to translate a word problem into an algebraic equation and solve it is a powerful skill that will serve you well throughout your academic and professional pursuits.
Latest Posts
Latest Posts
-
Birds That Start With Z
Sep 18, 2025
-
Warm Blooded Cold Blooded Animals
Sep 18, 2025
-
3 Out Of 4 Percentage
Sep 18, 2025
-
Specific Weight Vs Specific Gravity
Sep 18, 2025
-
Cracker Of The Year Awards
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Times 1.5 Is 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.