What Percent Is 1 9
seoindie
Sep 19, 2025 · 5 min read
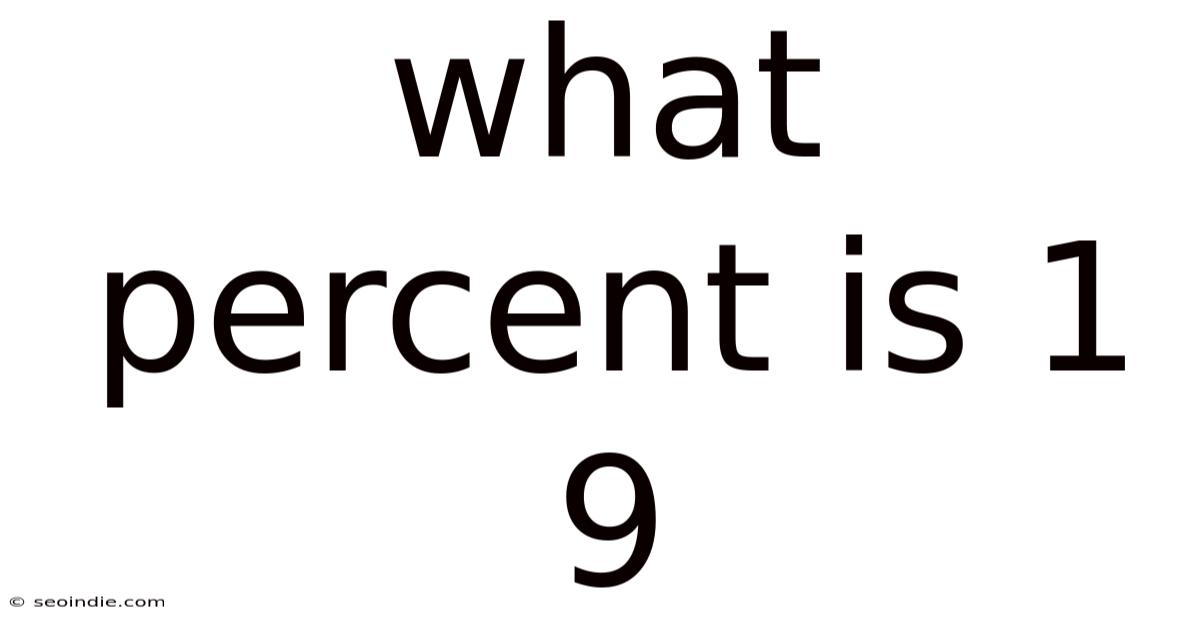
Table of Contents
What Percent is 1 of 9? Understanding Fractions, Decimals, and Percentages
This article will comprehensively explore the question "What percent is 1 of 9?" We'll move beyond simply providing the answer to delve into the underlying concepts of fractions, decimals, and percentages, equipping you with the tools to solve similar problems independently. Understanding these fundamental mathematical relationships is crucial for various applications, from everyday calculations to more advanced statistical analysis.
Understanding Fractions, Decimals, and Percentages
Before tackling the specific problem, let's review the core concepts:
-
Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) divided by a denominator (the bottom number). In our case, "1 of 9" is represented as the fraction 1/9.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. To convert a fraction to a decimal, you simply divide the numerator by the denominator.
-
Percentages: Percentages express a fraction or decimal as a portion of 100. The symbol "%" represents "per hundred." To convert a decimal to a percentage, multiply by 100 and add the "%" symbol. Conversely, to convert a percentage to a decimal, divide by 100.
Calculating the Percentage: Step-by-Step
Now, let's determine what percentage 1 is of 9:
Step 1: Express the relationship as a fraction.
As mentioned earlier, "1 of 9" is represented as the fraction 1/9.
Step 2: Convert the fraction to a decimal.
To convert 1/9 to a decimal, we divide the numerator (1) by the denominator (9):
1 ÷ 9 = 0.111111...
Notice that this decimal is a repeating decimal; the digit 1 repeats infinitely. For practical purposes, we'll often round this to a certain number of decimal places.
Step 3: Convert the decimal to a percentage.
To convert the decimal 0.111111... to a percentage, we multiply by 100:
0.111111... × 100 = 11.1111...%
Again, we have a repeating decimal. Depending on the level of precision required, we might round this to 11.11%, 11.1%, or even just 11%.
Therefore, 1 is approximately 11.11% of 9.
Understanding the Repeating Decimal
The repeating decimal 0.1111... (or 0.1̅) is a characteristic of some fractions. It means the digit 1 continues indefinitely. This is not a flaw in the calculation; it's a mathematical property of the fraction 1/9. The repeating nature highlights the limitations of representing some fractions precisely using a finite number of decimal places.
To illustrate this further, consider other fractions with 9 as the denominator:
- 2/9 = 0.2222... (0.2̅)
- 3/9 = 0.3333... (0.3̅)
- 4/9 = 0.4444... (0.4̅)
- and so on...
Notice the pattern: The numerator dictates the repeating digit in the decimal representation.
Practical Applications and Real-World Examples
Understanding percentages is crucial in numerous real-life situations:
-
Discounts and Sales: Stores often advertise discounts as percentages (e.g., "20% off"). This knowledge allows you to calculate the actual price reduction.
-
Taxes: Sales tax, income tax, and other taxes are typically expressed as percentages. Calculating the tax amount requires understanding percentage calculations.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Knowing how to calculate percentages is essential for managing finances effectively.
-
Statistical Analysis: Percentages are fundamental in statistical analysis, allowing for comparisons and interpretations of data. For instance, understanding survey results often involves working with percentages.
-
Grading Systems: Many educational systems use percentages to represent grades (e.g., 85% on a test).
-
Financial Reports: Businesses use percentages in financial reports to show profit margins, growth rates, and other key performance indicators.
Advanced Concepts: Proportions and Ratios
The problem of finding what percent 1 is of 9 can also be approached using the concept of proportions and ratios. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
1/9 = x/100
To solve for x, we cross-multiply:
9x = 100
x = 100/9
x ≈ 11.11%
This method provides an alternative approach to reach the same solution, reinforcing the interconnectedness of mathematical concepts.
Frequently Asked Questions (FAQ)
Q1: Why is 1/9 a repeating decimal?
A1: The fraction 1/9 is a repeating decimal because the denominator (9) cannot be expressed as a power of 10 (10, 100, 1000, etc.). Fractions whose denominators can be expressed as powers of 2 or 5 (or a combination of both) will result in terminating decimals (decimals that end). However, fractions with denominators containing prime factors other than 2 or 5 will often result in repeating decimals.
Q2: How accurate should my answer be?
A2: The accuracy required depends on the context. For everyday calculations, rounding to one or two decimal places (e.g., 11.11%) is usually sufficient. In scientific or engineering applications, greater precision might be necessary.
Q3: Can I use a calculator to solve this problem?
A3: Yes, a calculator can significantly simplify the process. Most calculators can handle decimal conversions and percentage calculations efficiently. However, understanding the underlying concepts is still crucial for problem-solving and interpreting results.
Q4: Are there any other ways to express 1/9?
A4: Yes, 1/9 can be expressed as a recurring decimal (0.111...), as a percentage (approximately 11.11%), or as a ratio (1:9). The most appropriate form depends on the specific application or context.
Conclusion: Mastering Percentages and Fractions
This in-depth exploration of "What percent is 1 of 9?" goes beyond a simple numerical answer. We've established a strong foundation in fractions, decimals, percentages, and their interrelationships. Understanding these concepts is not only important for solving mathematical problems but also for navigating numerous real-world situations involving discounts, taxes, interest rates, and much more. Remember that practice is key; applying these concepts to various problems will solidify your understanding and build confidence in your mathematical skills. By mastering these fundamental skills, you open doors to more complex mathematical concepts and problem-solving abilities.
Latest Posts
Latest Posts
-
Time Independent Schrodinger Wave Equation
Sep 20, 2025
-
Non Conservative And Conservative Forces
Sep 20, 2025
-
Inverse Of Product Of Matrices
Sep 20, 2025
-
Words With Vowel I Only
Sep 20, 2025
-
Gcf Of 36 And 42
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.