What Is A 4/5 Percentage
seoindie
Sep 12, 2025 · 5 min read
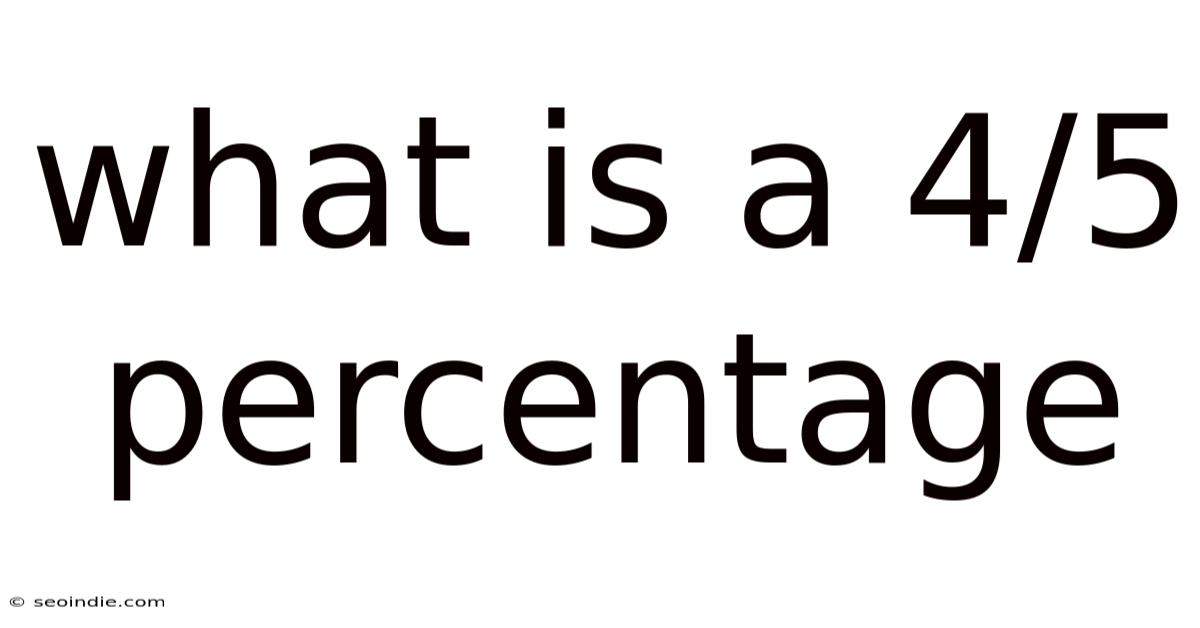
Table of Contents
Decoding the 4/5 Percentage: A Deep Dive into Fractions, Decimals, and Percentages
Understanding percentages is fundamental to navigating the world of mathematics and its applications in daily life. From calculating discounts in a store to understanding financial reports, percentages are everywhere. This article delves into the specific meaning of "4/5 percentage," explaining its representation as a fraction, decimal, and percentage, along with practical applications and common misconceptions. We'll explore the underlying concepts to solidify your understanding and equip you with the tools to confidently handle similar percentage calculations.
What Does 4/5 Mean?
Before diving into the percentage, let's clarify the meaning of the fraction 4/5. This is a simple fraction where:
- 4 (numerator): Represents the number of parts you have.
- 5 (denominator): Represents the total number of equal parts the whole is divided into.
This fraction indicates that you possess 4 out of 5 equal parts of a whole. Imagine a pizza cut into 5 slices; 4/5 represents having 4 of those slices.
Converting 4/5 to a Decimal
To convert the fraction 4/5 into a decimal, we simply perform the division: 4 ÷ 5 = 0.8. This means that 4/5 is equivalent to 0.8. Decimals are another way to represent parts of a whole, using the base-10 system. The decimal 0.8 signifies 8 tenths (8/10) of a whole.
Converting 4/5 to a Percentage
A percentage is a way of expressing a fraction or decimal as a portion of 100. To convert the fraction 4/5 or the decimal 0.8 to a percentage, we multiply by 100%:
0.8 × 100% = 80%
Therefore, 4/5 is equivalent to 80%. This means that 4/5 represents 80 parts out of 100 equal parts. This is a highly useful way to represent proportions, particularly in contexts involving comparisons and proportions.
Understanding the Concept of Percentage
A percentage is a dimensionless number; it doesn't have units. It signifies a ratio or proportion expressed as a fraction of 100. The percentage symbol (%) is used to indicate that the number is a percentage.
The fundamental formula for calculating a percentage is:
(Part / Whole) × 100% = Percentage
In the case of 4/5, the part is 4, and the whole is 5. Substituting these values into the formula confirms our earlier calculation:
(4 / 5) × 100% = 80%
Real-World Applications of 4/5 (or 80%)
The 4/5 percentage, or its equivalent 80%, appears frequently in various real-world scenarios:
- Grades and Scores: A student scoring 80% on a test has answered 4 out of every 5 questions correctly.
- Discounts and Sales: An 80% discount means an item is sold at 20% of its original price. This is because a discount of 80% leaves 20% of the original price remaining (100% - 80% = 20%).
- Surveys and Statistics: If 80% of respondents in a survey agree with a particular statement, it indicates that 4 out of every 5 respondents hold that opinion.
- Financial Calculations: Interest rates, profit margins, and many other financial calculations use percentages extensively. An 80% loan-to-value ratio means a loan amount is 80% of the asset's value.
- Progress Tracking: Project management often uses percentages to track progress. 80% completion means 4 out of 5 planned tasks are finished.
Common Misconceptions about Percentages
Several misconceptions often arise when dealing with percentages:
- Adding Percentages Directly: It's crucial to remember that percentages cannot be directly added unless they refer to the same whole. For example, a 20% increase followed by a 20% decrease does not result in the original value. The calculations need to be done sequentially based on the changing base values.
- Percentage Increase/Decrease from Different Bases: A percentage increase or decrease is always relative to the original value. A 10% increase on $100 is different from a 10% increase on $200.
- Confusing Percentage Points with Percentages: A change from 20% to 30% is a 10 percentage point increase, not a 50% increase. The percentage increase is calculated as [(30-20)/20] * 100% = 50%. This distinction is critical for accurate interpretation.
Advanced Applications and Calculations Involving 4/5
While the basic concepts are straightforward, let's explore more advanced scenarios:
- Calculating 80% of a Number: To find 80% of a number, multiply the number by 0.8 (the decimal equivalent of 80%). For example, 80% of 500 is 500 × 0.8 = 400.
- Finding the Original Value after a Percentage Change: If a value has been increased or decreased by a certain percentage, you can find the original value using reverse calculations. For example, if a number increased by 20% to reach 60, then the original number was 60 / 1.20 = 50.
- Compounding Percentages: When percentages are applied repeatedly, such as compound interest, the calculations become more complex, requiring careful attention to the compounding periods and the interest rate.
Frequently Asked Questions (FAQs)
Q1: Is 4/5 the same as 80%?
A1: Yes, absolutely. 4/5, 0.8, and 80% are all different representations of the same value.
Q2: How do I convert a percentage to a fraction?
A2: Divide the percentage by 100 and simplify the resulting fraction. For example, to convert 60% to a fraction, divide 60 by 100 to get 60/100. This simplifies to 3/5.
Q3: How do I convert a decimal to a percentage?
A3: Multiply the decimal by 100 and add the percentage symbol (%). For example, 0.75 becomes 0.75 × 100% = 75%.
Q4: What if I have a more complex fraction, say 12/15? How would I convert that to a percentage?
A4: First, simplify the fraction if possible (12/15 simplifies to 4/5). Then, follow the same steps as outlined earlier: divide the numerator by the denominator (4 ÷ 5 = 0.8) and then multiply by 100% (0.8 × 100% = 80%).
Conclusion
Understanding the concept of 4/5 percentage, its representation as a fraction, decimal, and percentage, and its practical applications is crucial for navigating numerous aspects of daily life and professional endeavors. By grasping the underlying principles and practicing the conversion methods, you can confidently handle percentage calculations and interpret data accurately. Remember to avoid common misconceptions and utilize the provided formulas and examples to reinforce your understanding. Mastering percentages is a valuable skill that will empower you to make informed decisions and tackle more complex mathematical problems.
Latest Posts
Latest Posts
-
2025 Word Of The Year
Sep 12, 2025
-
Definition Of A Graduated Cylinder
Sep 12, 2025
-
Pi 6 Rad To Degrees
Sep 12, 2025
-
Molar Mass Of Potassium Ferricyanide
Sep 12, 2025
-
Una Yarda Cuantos Pies Tiene
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is A 4/5 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.