What Is 3/4 In Percentage
seoindie
Sep 17, 2025 · 5 min read
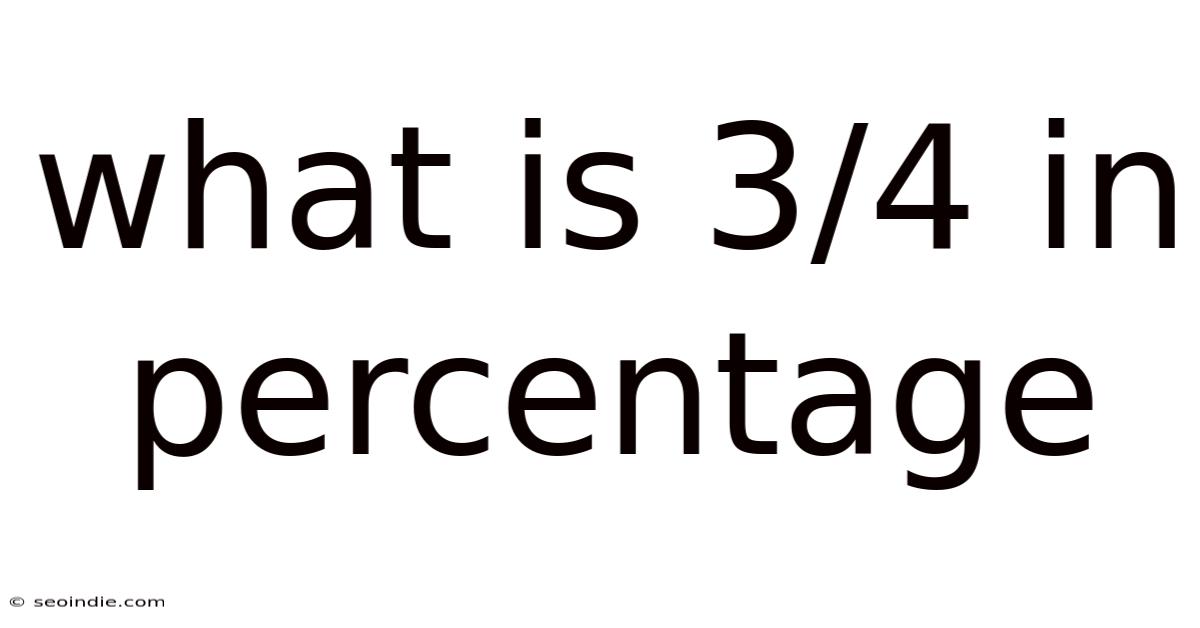
Table of Contents
What is 3/4 in Percentage? A Comprehensive Guide
Fractions and percentages are fundamental concepts in mathematics, crucial for everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will explore how to convert the fraction 3/4 into a percentage, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also tackle common related questions and provide practical examples to solidify your understanding. By the end, you’ll not only know the answer but also grasp the broader context of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." Percentages are widely used because they offer a standardized way to compare proportions. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 3/4 to a Percentage: The Step-by-Step Process
There are two primary methods to convert the fraction 3/4 into a percentage:
Method 1: Using the Decimal Equivalent
-
Divide the numerator by the denominator: Divide 3 by 4. This gives you 0.75.
-
Multiply the decimal by 100: Multiply 0.75 by 100. This results in 75.
-
Add the percentage symbol: Add the "%" symbol to indicate that the result is a percentage.
Therefore, 3/4 is equal to 75%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
-
Find a multiplier: Determine what number you need to multiply the denominator (4) by to get 100. In this case, 4 multiplied by 25 equals 100.
-
Multiply both the numerator and the denominator: Multiply both the numerator (3) and the denominator (4) by 25. This gives you 75/100.
-
Express as a percentage: Since a percentage is a fraction out of 100, 75/100 is directly equivalent to 75%.
Why These Methods Work: A Deeper Look at the Mathematics
The reason these methods work lies in the fundamental relationship between fractions, decimals, and percentages. They are all different ways of representing the same proportion.
-
Fractions to Decimals: Dividing the numerator by the denominator converts a fraction into its decimal equivalent. This decimal represents the fraction's value as a part of one whole.
-
Decimals to Percentages: Multiplying a decimal by 100 scales the decimal up to represent the fraction as a part of 100, which is the essence of a percentage.
-
Fractions to Percentages (Method 2): Creating an equivalent fraction with a denominator of 100 directly gives the percentage because the numerator then represents the number "out of 100."
Practical Applications of Converting 3/4 to 75%
The conversion of 3/4 to 75% has countless applications in everyday life and various fields. Here are a few examples:
-
Sales and Discounts: A store offering a 75% discount is offering a discount equal to 3/4 of the original price.
-
Financial Calculations: Interest rates, profit margins, and other financial figures are often expressed as percentages. Understanding fraction-to-percentage conversions is vital for interpreting and working with this data.
-
Data Analysis: Statistical data often involve proportions that can be represented as fractions and then converted to percentages for clearer presentation and comparison.
-
Measurement and Proportion: If you are working with recipes, building plans, or any situation requiring precise proportions, understanding fraction-to-percentage conversions can be incredibly helpful.
Commonly Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
A1: Yes, absolutely! The methods described above apply to any fraction. You simply divide the numerator by the denominator to get the decimal equivalent and then multiply by 100 to obtain the percentage.
Q2: What if the fraction results in a repeating decimal?
A2: Some fractions result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can either round the decimal to a certain number of decimal places before multiplying by 100, or you can leave the percentage as a fraction (e.g., 33.33% or 1/3 as a percentage).
Q3: What about improper fractions (where the numerator is larger than the denominator)?
A3: Improper fractions will result in percentages greater than 100%. This is perfectly valid and simply means that you have more than one whole. For example, 5/4 would be 125%.
Q4: Are there any online calculators or tools to help with this conversion?
A4: While I cannot provide links to external websites, a quick online search for "fraction to percentage calculator" will reveal numerous free tools that can perform this conversion for you. However, understanding the underlying process is crucial for building mathematical confidence and problem-solving skills.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with widespread applications. Understanding the underlying mathematical principles, as well as the step-by-step processes, empowers you to confidently tackle various problems involving proportions and ratios in different contexts. The conversion of 3/4 to 75% serves as a clear and practical example of this crucial mathematical skill. Whether you're working on a simple shopping discount or a complex financial model, the ability to seamlessly convert fractions to percentages is an invaluable asset. Remember to practice regularly to strengthen your understanding and build fluency in this important area of mathematics.
Latest Posts
Latest Posts
-
Ammonium Nitrate Acid Or Base
Sep 17, 2025
-
Genetic Drift Example In Animals
Sep 17, 2025
-
Lcm For 9 12 15
Sep 17, 2025
-
Concept Map For Cellular Respiration
Sep 17, 2025
-
List Of Factors Of 20
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.