What Is 3/4 In Percent
seoindie
Sep 10, 2025 · 5 min read
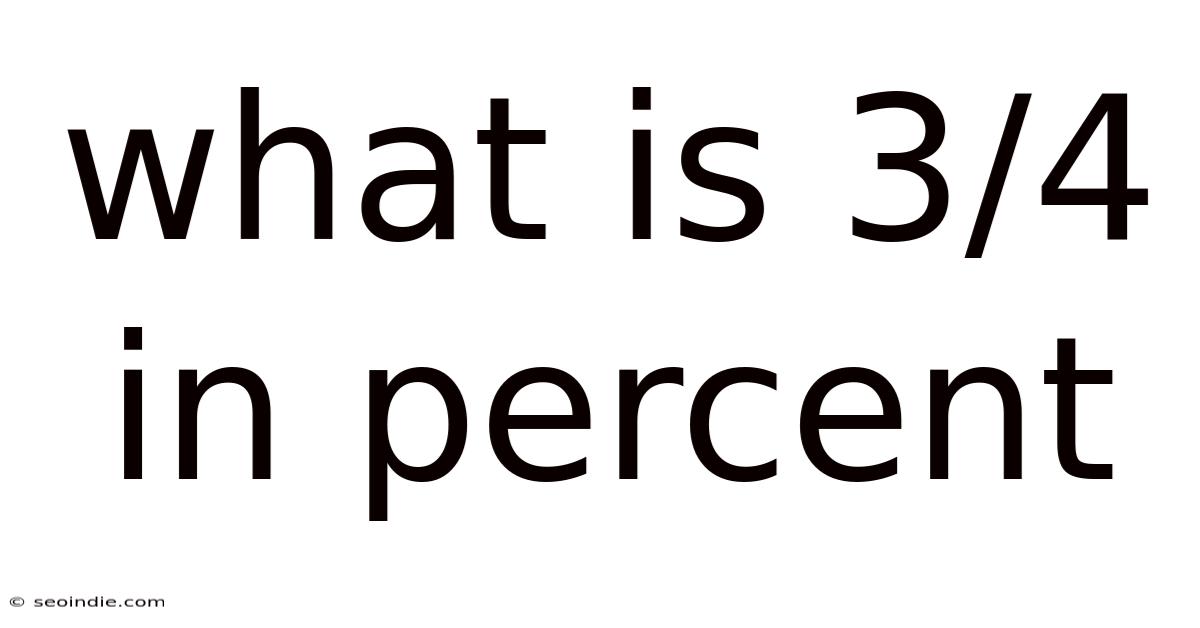
Table of Contents
What is 3/4 in Percent? A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the conversion of the fraction 3/4 into a percentage, explaining the process in detail, exploring the underlying mathematical principles, and providing practical examples to solidify your understanding. We'll also address frequently asked questions and offer further resources for continued learning.
Introduction: Fractions, Decimals, and Percentages – A Unified Concept
Before we jump into converting 3/4 to a percentage, let's briefly review the interconnectedness of fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction expresses a part of a whole as a ratio of two numbers (numerator/denominator). A decimal represents a fraction where the denominator is a power of 10. A percentage expresses a fraction as a proportion of 100. Understanding this interconnectedness is crucial for smooth transitions between these representations.
Converting 3/4 to a Percentage: Step-by-Step Guide
The conversion of 3/4 to a percentage involves two primary methods:
Method 1: Direct Conversion using Division
This method involves dividing the numerator (3) by the denominator (4) to obtain a decimal, then multiplying the result by 100 to express it as a percentage.
-
Divide the numerator by the denominator: 3 ÷ 4 = 0.75
-
Multiply the decimal by 100: 0.75 x 100 = 75
-
Add the percentage symbol: 75%
Therefore, 3/4 is equal to 75%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the definition of percentage as "per hundred." We aim to find an equivalent fraction of 3/4 that has a denominator of 100.
-
Determine the multiplication factor: To transform the denominator 4 into 100, we multiply it by 25 (100 ÷ 4 = 25).
-
Multiply both the numerator and the denominator by the same factor: (3 x 25) / (4 x 25) = 75/100
-
Express as a percentage: Since 75/100 means 75 out of 100, this is equivalent to 75%.
This method clearly illustrates the meaning of percentage: 75 parts out of 100 parts.
Understanding the Mathematical Principles Behind the Conversion
The conversion from a fraction to a percentage relies on the fundamental concept of proportion. A percentage is simply a fraction where the denominator is fixed at 100. The process of conversion involves finding an equivalent fraction with a denominator of 100, which represents the same proportion as the original fraction. This equivalence is maintained because we multiply both the numerator and denominator by the same factor, ensuring the ratio remains constant. The multiplication by 100 in Method 1 achieves the same result, effectively scaling the decimal representation to a percentage.
Practical Applications of 3/4 (75%) in Real-World Scenarios
The understanding of 3/4 as 75% has numerous practical applications across various fields:
-
Sales and Discounts: A 75% discount on an item means you pay only 25% of the original price. This is commonly seen during sales events and clearance sales.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are frequently expressed as percentages. Understanding fractions like 3/4 as 75% is crucial for accurate financial planning and analysis.
-
Data Interpretation: Charts and graphs often represent data as percentages, making it easier to visualize and understand proportions. The ability to convert fractions to percentages enables effective interpretation of such visual representations.
-
Scientific and Engineering Calculations: Percentages are widely used in various scientific and engineering fields, such as expressing efficiency, accuracy, and error margins. Converting fractions to percentages facilitates calculations and analysis in these areas.
-
Everyday Life: Many everyday tasks involve percentages, including calculating tips, splitting bills, or understanding nutritional information on food labels. Converting fractions such as 3/4 to a percentage simplifies these calculations.
Beyond 3/4: Converting Other Fractions to Percentages
The methods described above can be applied to any fraction. The general formula is:
(Numerator ÷ Denominator) x 100 = Percentage
For instance, to convert 2/5 to a percentage:
-
2 ÷ 5 = 0.4
-
0.4 x 100 = 40%
Therefore, 2/5 is equal to 40%.
Similarly, for converting 1/8:
-
1 ÷ 8 = 0.125
-
0.125 x 100 = 12.5%
Therefore, 1/8 is equal to 12.5%.
Frequently Asked Questions (FAQ)
Q: What if the fraction results in a recurring decimal?
A: If the division results in a recurring decimal (e.g., 1/3 = 0.333...), you can either round the decimal to a certain number of decimal places before multiplying by 100, or express the percentage with a recurring decimal (e.g., 33.333...). The level of precision depends on the context of the problem.
Q: Can I convert percentages back to fractions?
A: Yes, absolutely! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% can be converted to a fraction as follows: 60/100 = 3/5.
Q: Why is understanding percentage conversion important?
A: Percentage conversion is crucial for understanding proportions, making comparisons, and solving problems across various fields. It's a fundamental skill with wide-ranging applications in everyday life, academics, and professional settings.
Q: Are there any online tools or calculators that can help with fraction to percentage conversion?
A: While this article does not endorse external websites, a simple search on your preferred search engine for "fraction to percentage calculator" will yield multiple results of free online tools that can facilitate the conversion. However, understanding the underlying mathematical principles is still crucial for true comprehension and problem-solving abilities.
Conclusion: Mastering Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a critical mathematical skill with numerous real-world applications. By mastering the methods outlined in this guide, you'll be equipped to confidently handle fraction-to-percentage conversions and apply this knowledge to solve problems in various contexts. Remember the key steps: divide the numerator by the denominator, then multiply the result by 100 to obtain the percentage equivalent. Practice regularly with different fractions to solidify your understanding and build confidence. This skill is foundational to numerous mathematical and real-world applications and will significantly enhance your quantitative reasoning abilities. Continue practicing and exploring related concepts to expand your mathematical proficiency.
Latest Posts
Latest Posts
-
How Many State For India
Sep 10, 2025
-
Mixed To Improper Fraction Calculator
Sep 10, 2025
-
150 Square Meters To Feet
Sep 10, 2025
-
The Primary Photosynthetic Pigment Is
Sep 10, 2025
-
Win Loss Tie Percentage Calculator
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.