The Square Root Of 121
seoindie
Sep 20, 2025 · 6 min read
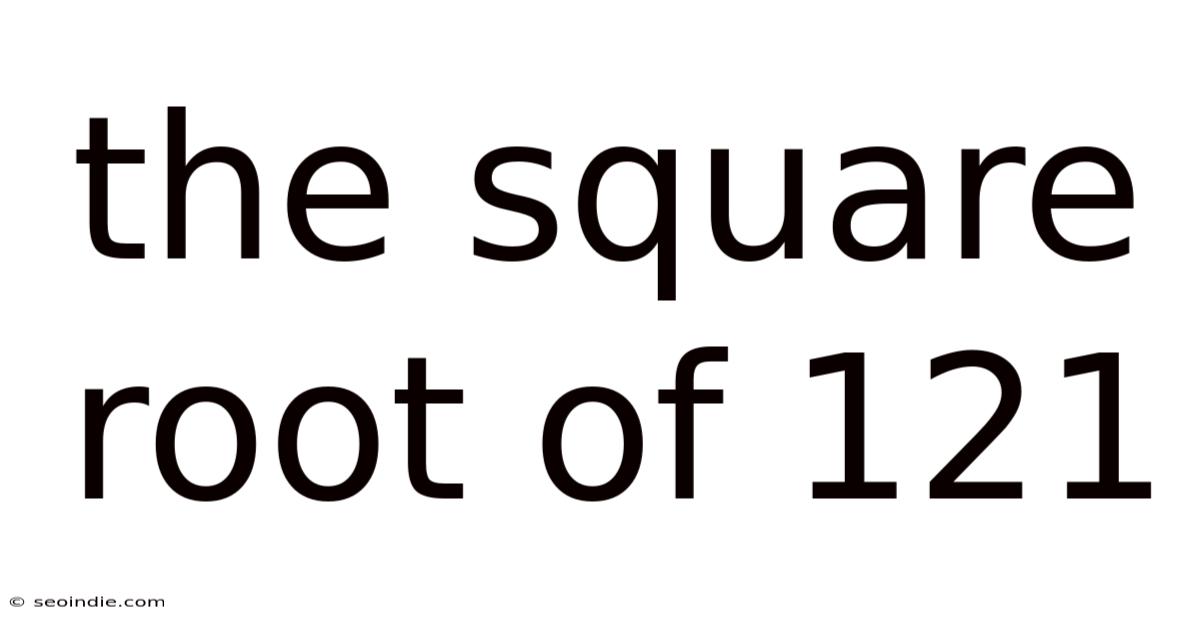
Table of Contents
Unveiling the Mysteries of the Square Root of 121: A Deep Dive into Numbers
Finding the square root of 121 might seem like a simple arithmetic problem, suitable only for elementary school students. However, delving deeper reveals a fascinating journey into the world of mathematics, touching upon concepts relevant to algebra, geometry, and even computer science. This exploration won't just provide the answer – it will illuminate the underlying principles and expand your understanding of square roots and their significance. This article will cover the basics, explore various methods of calculation, and delve into the broader mathematical context of square roots.
Understanding Square Roots: A Fundamental Concept
Before we tackle the square root of 121 specifically, let's establish a firm grasp of what a square root actually is. In simple terms, the square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This relationship can be represented mathematically as √9 = 3, where the symbol '√' denotes the square root.
Square roots are the inverse operation of squaring a number. Squaring a number means multiplying it by itself. If we square 5 (5²), we get 25. Conversely, the square root of 25 (√25) is 5. This fundamental relationship underlies many mathematical concepts and applications.
Calculating the Square Root of 121: Multiple Approaches
Now, let's address the main question: what is the square root of 121? The most straightforward approach is to recall the multiplication tables. If you remember your times tables well, you'll quickly realize that 11 multiplied by itself (11²) equals 121. Therefore, the square root of 121 is 11.
However, not all numbers have such easily recognizable square roots. For larger numbers or those without readily apparent factors, several other methods can be employed:
-
Prime Factorization: This method involves breaking down the number into its prime factors. While not the most efficient method for 121, it's helpful for understanding the concept. 121 can be factored as 11 x 11. Since we have a pair of identical factors (11 and 11), the square root is simply one of those factors – 11.
-
Estimation and Iteration: For larger numbers without readily apparent square roots, estimation and iterative methods become valuable. You can start by estimating the square root, then refine your estimate through successive calculations. For instance, you might guess that the square root of 121 is around 10. Squaring 10 gives you 100, which is close to 121. Trying 11, you find the exact answer. This method is particularly useful when dealing with non-perfect squares (numbers whose square roots are not whole numbers).
-
Using a Calculator: Modern calculators have a dedicated square root function (√). Simply input 121 and press the square root button to obtain the answer: 11. This is the most convenient method for everyday calculations.
-
Newton-Raphson Method: This is a powerful iterative method for finding the roots of equations, including square roots. It involves repeatedly refining an initial guess using a specific formula until the desired level of accuracy is reached. While more complex than the previous methods, the Newton-Raphson method is crucial in numerical analysis and computer science for approximating square roots of very large or complex numbers.
The Geometric Interpretation of Square Roots
The concept of a square root extends beyond mere numerical calculation. It has a strong geometric interpretation. Consider a square with an area of 121 square units. The square root of 121 represents the length of one side of this square. Since 11 x 11 = 121, the side length of the square is 11 units. This geometric visualization offers a concrete understanding of the concept, especially for visual learners.
This geometric interpretation extends to other shapes and dimensions. For example, finding the cube root of a number represents the length of the side of a cube with that volume. This visual connection reinforces the mathematical concepts involved.
Square Roots in the Broader Mathematical Landscape
Square roots are not isolated concepts; they are fundamental building blocks in various areas of mathematics:
-
Algebra: Square roots are frequently used in solving quadratic equations (equations of the form ax² + bx + c = 0). The quadratic formula, a crucial tool for solving these equations, directly involves square roots.
-
Trigonometry: Trigonometric functions, such as sine, cosine, and tangent, often involve square roots in their definitions and calculations, particularly when dealing with right-angled triangles.
-
Calculus: Derivatives and integrals of functions often involve square roots, particularly in optimization problems and calculations of areas and volumes.
-
Number Theory: Square roots play a role in number theory, particularly in the study of perfect squares, Pythagorean triples, and Diophantine equations.
-
Physics and Engineering: Square roots appear in countless physics and engineering applications, from calculating distances and velocities to analyzing forces and energies. For instance, the calculation of speed often involves the square root of the sum of squares of components.
-
Computer Science: Efficient algorithms for calculating square roots are crucial in computer graphics, simulations, and other computationally intensive applications. The Newton-Raphson method, mentioned earlier, is a prime example of such an algorithm.
Frequently Asked Questions (FAQs)
Q: Is the square root of 121 a rational or irrational number?
A: The square root of 121 (11) is a rational number. Rational numbers can be expressed as a fraction of two integers (in this case, 11/1). Irrational numbers, like the square root of 2, cannot be expressed as a simple fraction.
Q: What is the difference between √121 and ±√121?
A: √121 refers to the principal square root, which is the positive square root (11). ±√121 represents both the positive and negative square roots (+11 and -11), since both (-11)² and (11)² equal 121. The context usually determines whether you need the principal root or both roots.
Q: How can I calculate the square root of a negative number?
A: The square root of a negative number is not a real number. It involves the concept of imaginary numbers, denoted by the symbol 'i', where i² = -1. For example, √-1 = i, and √-121 = 11i. Imaginary numbers are crucial in advanced mathematics and physics.
Q: Are there other methods to calculate square roots besides the ones mentioned?
A: Yes, there are several other methods, including various numerical algorithms and series expansions. These methods are often more computationally intensive but provide increased accuracy and efficiency for specific applications. The Babylonian method, for instance, is an ancient iterative method for approximating square roots.
Q: Why are square roots important?
A: Square roots are fundamental mathematical concepts with widespread applications across numerous fields. Their importance stems from their connection to numerous mathematical operations, geometrical concepts, and their role in solving equations and modeling real-world phenomena.
Conclusion: Beyond the Simple Answer
While the answer to the question "What is the square root of 121?" is simply 11, this exploration has revealed a much richer mathematical landscape. From the basic arithmetic operation to its geometric interpretation and its profound significance in various branches of mathematics and science, the square root of 121 serves as a gateway to understanding more complex concepts. This detailed analysis underscores the importance of not just finding the answer, but also understanding the underlying principles and appreciating the broader context of mathematical ideas. Hopefully, this deep dive has not only provided you with the answer but also ignited your curiosity and encouraged further exploration of the fascinating world of mathematics.
Latest Posts
Latest Posts
-
C Words To Describe People
Sep 21, 2025
-
How Tall Is 35 Cm
Sep 21, 2025
-
How Tall Is 168 Centimeters
Sep 21, 2025
-
What Equals 22 In Multiplication
Sep 21, 2025
-
What Are Primary Economic Activities
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about The Square Root Of 121 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.