Square Root Of 9 Simplified
seoindie
Sep 14, 2025 · 6 min read
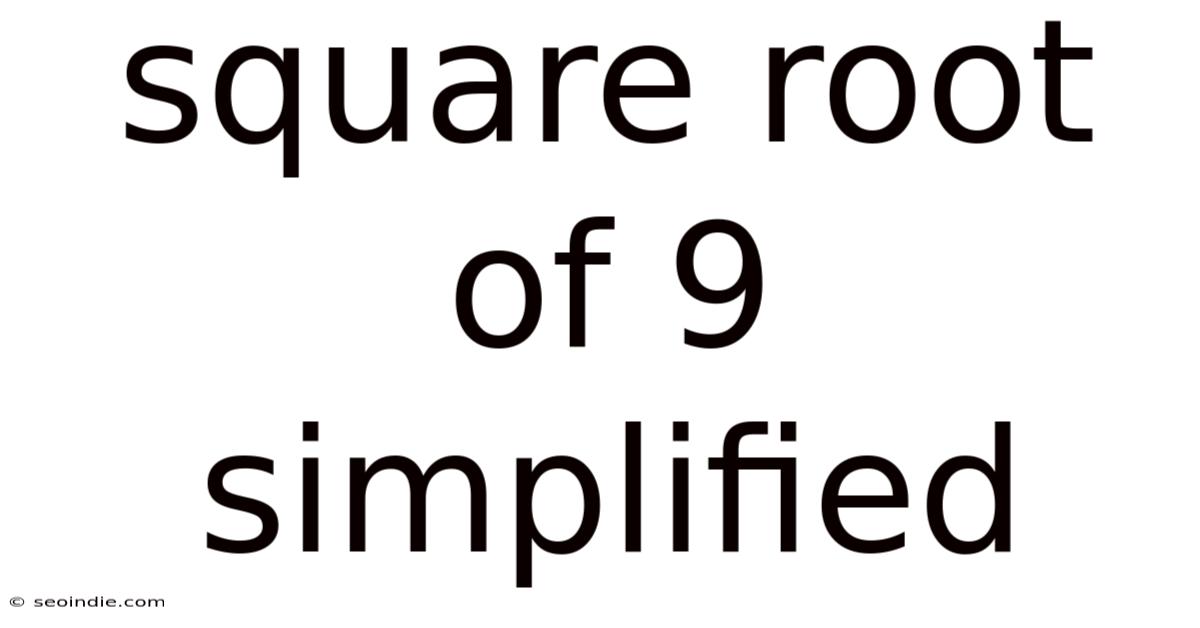
Table of Contents
Understanding and Simplifying the Square Root of 9: A Comprehensive Guide
The square root of 9, often written as √9, is a fundamental concept in mathematics that appears frequently in various fields, from basic arithmetic to advanced calculus. This seemingly simple calculation opens doors to a deeper understanding of numbers, their properties, and their relationships. This comprehensive guide will not only show you how to simplify √9 but also delve into the broader context of square roots, explaining their meaning, applications, and even exploring some related mathematical concepts. We’ll cover everything from the basics to more advanced ideas, ensuring a thorough and engaging learning experience.
What is a Square Root?
Before we tackle √9 specifically, let's establish a clear understanding of what a square root actually is. In simple terms, the square root of a number is a value that, when multiplied by itself, gives the original number. Think of it as the inverse operation of squaring a number. When we square a number (raise it to the power of 2), we multiply it by itself. For example:
- 2² = 2 x 2 = 4
- 3² = 3 x 3 = 9
- 5² = 5 x 5 = 25
Therefore, the square root of 4 (√4) is 2, because 2 x 2 = 4. Similarly, the square root of 25 (√25) is 5.
Calculating the Square Root of 9
Now, let's address the main topic: simplifying √9. Given our definition of a square root, we are looking for a number that, when multiplied by itself, equals 9. The answer is straightforward:
√9 = 3
This is because 3 x 3 = 9. There's no other positive number that satisfies this condition. It's important to note that while (-3) x (-3) also equals 9, we typically focus on the principal square root, which is the non-negative root. In most mathematical contexts, unless otherwise specified, √9 refers to the positive value, 3.
Beyond the Basics: Exploring Properties of Square Roots
Understanding the square root of 9 is just the first step. Let's delve into some more advanced properties of square roots that will enhance your comprehension of this mathematical concept.
1. Square Roots of Perfect Squares:
Numbers like 9, 25, 100, and so on, are called perfect squares because they are the result of squaring an integer. Finding the square root of a perfect square is relatively simple, as it will always be an integer. For example:
- √16 = 4 (because 4 x 4 = 16)
- √49 = 7 (because 7 x 7 = 49)
- √144 = 12 (because 12 x 12 = 144)
2. Square Roots of Non-Perfect Squares:
Not all numbers are perfect squares. When dealing with the square root of a non-perfect square (e.g., √2, √5, √17), the result is an irrational number. Irrational numbers cannot be expressed as a simple fraction and their decimal representation goes on forever without repeating. These are often approximated using calculators or other computational methods.
3. Simplifying Square Roots with Radicals:
When dealing with larger numbers or expressions involving square roots, we can often simplify them by factoring. This involves finding perfect square factors within the number under the radical sign (√). For example:
- √12 = √(4 x 3) = √4 x √3 = 2√3
Here, we factored 12 into 4 (a perfect square) and 3. We can then simplify √4 to 2, leaving the √3. This simplified form, 2√3, is often preferred because it's more concise and easier to work with in calculations.
4. Operations with Square Roots:
Square roots obey certain rules when performing addition, subtraction, multiplication, and division.
- Multiplication: √a x √b = √(a x b) (e.g., √4 x √9 = √36 = 6)
- Division: √a / √b = √(a / b) (e.g., √9 / √4 = √(9/4) = 3/2)
- Addition/Subtraction: You can only add or subtract square roots that have the same radicand (the number inside the square root symbol). For example, 2√3 + 5√3 = 7√3, but 2√3 + 5√2 cannot be simplified further.
Applications of Square Roots
The concept of square roots extends far beyond simple calculations. It plays a crucial role in numerous fields, including:
- Geometry: Calculating the lengths of sides in right-angled triangles using the Pythagorean theorem (a² + b² = c²), which heavily relies on square roots.
- Physics: Used in various formulas related to motion, energy, and other physical phenomena. For example, calculating the velocity of an object using the formula v = √(2gh) (where g is acceleration due to gravity and h is the height).
- Engineering: In structural design, electrical engineering, and many other engineering disciplines where calculations involve distances, forces, and other quantities.
- Computer Graphics: Used extensively in algorithms for rendering images and manipulating 2D and 3D models.
- Statistics: In calculating standard deviation and variance, important measures of data dispersion.
Frequently Asked Questions (FAQs)
Q1: What is the difference between a square root and a square?
A square is the result of multiplying a number by itself (e.g., 3² = 9). A square root is the inverse operation; it's the number that, when multiplied by itself, gives the original number (e.g., √9 = 3).
Q2: Can a square root be negative?
While (-3)² = 9, the principal square root (the one usually denoted by the √ symbol) is always non-negative. However, equations like x² = 9 will have two solutions: x = 3 and x = -3.
Q3: How do I calculate the square root of a number without a calculator?
For perfect squares, you can usually find the answer mentally by remembering multiplication tables. For non-perfect squares, methods like the Babylonian method (a type of iterative approximation) or using logarithm tables (an older method) can be used. However, calculators are the most convenient tool for most cases.
Q4: Are there other types of roots besides square roots?
Yes, there are cube roots (∛), fourth roots (∜), and nth roots (ⁿ√), where n represents any positive integer. The nth root of a number is a value that, when multiplied by itself n times, gives the original number.
Q5: What happens if I take the square root of a negative number?
Taking the square root of a negative number in the real number system results in an imaginary number. Imaginary numbers are denoted using the symbol i, where i² = -1. For example, √(-9) = 3i.
Conclusion: Mastering the Square Root of 9 and Beyond
While seemingly simple, the square root of 9 represents a gateway to a much broader understanding of fundamental mathematical concepts. From comprehending perfect squares and irrational numbers to applying square roots in various fields, this seemingly simple calculation opens doors to more complex mathematical ideas and their real-world applications. By mastering the basics and understanding the properties of square roots, you'll build a strong foundation for tackling more challenging mathematical problems in the future. Remember, mathematics is a journey of continuous learning, and each step, like understanding √9, brings you closer to a deeper appreciation of the elegance and power of numbers.
Latest Posts
Latest Posts
-
Is Amoeba Prokaryote Or Eukaryote
Sep 14, 2025
-
Christmas Things Starting With F
Sep 14, 2025
-
Location Of Elastic Connective Tissue
Sep 14, 2025
-
Difference Between Echo And Reverberation
Sep 14, 2025
-
Polar To Rectangular Form Calculator
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 9 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.