Square Root Of 5 2
seoindie
Sep 19, 2025 · 5 min read
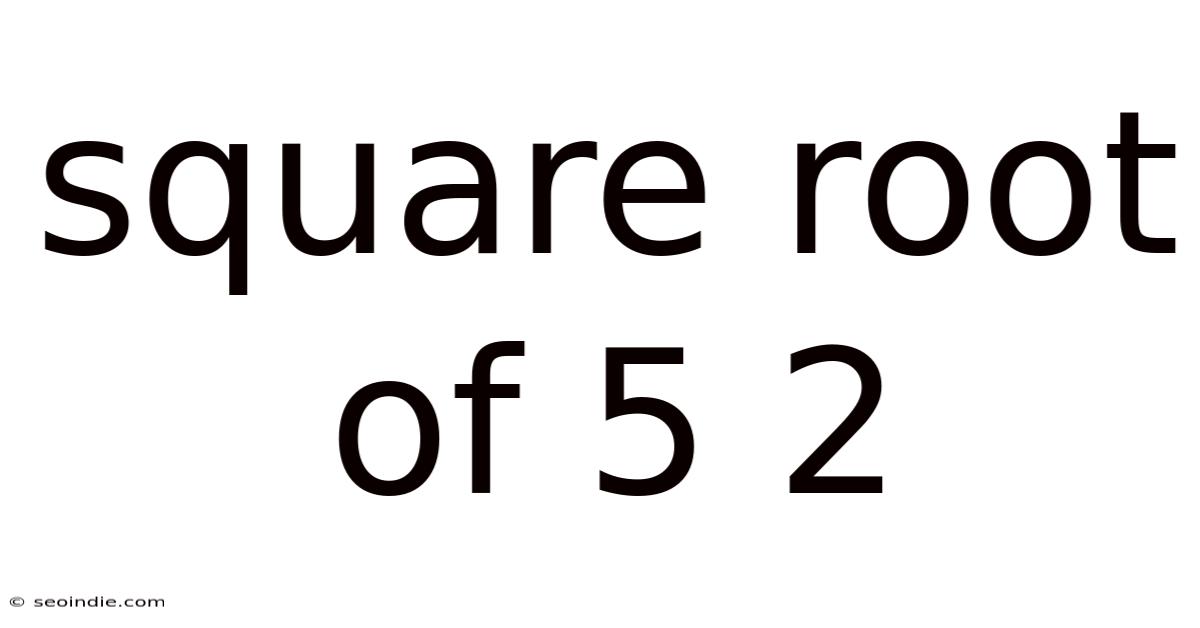
Table of Contents
Decoding the Mysteries of the Square Root of 5: A Deep Dive into √5
The square root of 5, denoted as √5, is a fascinating number that bridges the gap between pure mathematics and practical applications. It's an irrational number, meaning it cannot be expressed as a simple fraction, and its decimal representation continues infinitely without repeating. This seemingly simple concept opens up a world of exploration, encompassing geometry, algebra, number theory, and even computer science. This article delves deep into the intricacies of √5, exploring its properties, calculations, applications, and its place within the broader mathematical landscape.
Understanding Square Roots: A Quick Refresher
Before embarking on our journey into the world of √5, let's refresh our understanding of square roots. The square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. This concept is fundamental to many areas of mathematics and has far-reaching consequences.
Calculating the Square Root of 5: Methods and Approaches
Calculating √5 precisely is impossible because it's irrational. However, we can approximate its value using various methods:
1. The Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method provides a highly efficient way to approximate square roots. It's an iterative process, meaning we repeat a set of steps to refine our approximation. Here's how it works for √5:
-
Start with an initial guess: Let's start with 2, as 2 x 2 = 4, which is close to 5.
-
Improve the guess: Divide 5 by our initial guess (5/2 = 2.5).
-
Average the results: Average the initial guess and the result from step 2: (2 + 2.5) / 2 = 2.25.
-
Repeat: Now use 2.25 as the new guess and repeat steps 2 and 3. This process is repeated until the desired level of accuracy is achieved.
By repeating this process, we can get progressively closer to the actual value of √5. After several iterations, we obtain a highly accurate approximation. The Babylonian method demonstrates the power of iterative processes in numerical analysis.
2. Using a Calculator or Computer Software
Modern calculators and computer software readily provide approximations of √5 to numerous decimal places. This method is the most straightforward and efficient for practical purposes. However, understanding the underlying principles, as demonstrated by the Babylonian method, provides a deeper appreciation for the mathematical concepts involved.
3. Continued Fractions: An Elegant Representation
√5 can also be represented as a continued fraction, which offers an infinite series of fractions that converge towards the true value. The continued fraction for √5 is:
2 + 1/(4 + 1/(4 + 1/(4 + ...)))
This representation is not only mathematically elegant but also highlights the inherent complexity of irrational numbers. Each term in the continued fraction improves the approximation, providing a unique perspective on the nature of √5.
The Golden Ratio and its Connection to √5
The Golden Ratio (φ), approximately 1.618, is a ubiquitous number in mathematics, art, and nature. It has a profound relationship with √5. The Golden Ratio can be expressed precisely as:
φ = (1 + √5) / 2
This formula demonstrates the fundamental connection between the seemingly simple √5 and the aesthetically pleasing Golden Ratio. This link extends to various geometric constructions, such as the Golden Rectangle and the Fibonacci sequence, where √5 plays a pivotal role.
Geometric Applications of √5: The Diagonal of a Rectangle
√5 appears naturally in geometric contexts. Consider a rectangle with sides of length 1 and 2. Using the Pythagorean theorem (a² + b² = c²), we find that the diagonal of this rectangle has a length of √(1² + 2²) = √5. This simple example showcases how √5 emerges organically within geometric calculations.
√5 in Algebra and Number Theory
√5 plays a significant role in algebraic number theory. It is a key element in certain algebraic fields and extensions of the rational numbers. It's a crucial component in analyzing quadratic equations and solving various algebraic problems. Its properties as an irrational number lead to unique algebraic structures and properties.
Applications in Physics and Engineering: Unexpected Occurrences
While not as prominent as other mathematical constants like π (pi) or e (Euler's number), √5 subtly appears in various physical and engineering applications. For instance, it is encountered in certain calculations involving mechanics, vibrations, and wave phenomena. Its presence often emerges unexpectedly during problem-solving, highlighting its fundamental place within the mathematical framework of the physical world.
Approximating √5: Accuracy and Precision
The level of accuracy needed when approximating √5 depends on the application. For many practical purposes, a simple approximation like 2.236 is sufficient. However, for more demanding applications like scientific computations or engineering designs, higher precision might be necessary, demanding more iterations in methods like the Babylonian method or utilizing the capabilities of computational software.
Frequently Asked Questions (FAQs)
Q: Is √5 a rational number?
A: No, √5 is an irrational number. It cannot be expressed as a fraction of two integers.
Q: What is the exact value of √5?
A: There is no exact decimal representation of √5. Its decimal expansion is non-terminating and non-repeating.
Q: How can I calculate √5 without a calculator?
A: You can use methods like the Babylonian method or continued fractions to approximate √5. However, these methods require iterative calculations.
Q: What are the practical applications of √5?
A: √5 has applications in geometry, algebra, number theory, and certain areas of physics and engineering.
Conclusion: A Number with Profound Implications
The square root of 5, though seemingly a simple concept, unravels into a complex and fascinating mathematical entity. Its appearance in various fields, from geometry to algebra to even unexpected places in physics and engineering, highlights its fundamental role within the broader mathematical framework. Whether approximated using ancient methods or calculated with modern tools, √5 continues to challenge and inspire mathematicians and scientists alike, reminding us of the elegant and intricate beauty of numbers. Its connection to the Golden Ratio further underscores its significant place within the history and application of mathematical concepts. Understanding √5 isn't just about knowing its numerical value; it's about grasping its inherent properties, its historical significance, and its widespread influence across diverse scientific disciplines.
Latest Posts
Latest Posts
-
What Is 1 5kg In Pounds
Sep 19, 2025
-
Words That Start With Pf
Sep 19, 2025
-
Nouns That Start With Ap
Sep 19, 2025
-
Types Of Patterns Fine Print
Sep 19, 2025
-
How Many Feet Is 90cm
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.