Square Root Of 225 Simplified
seoindie
Sep 21, 2025 · 6 min read
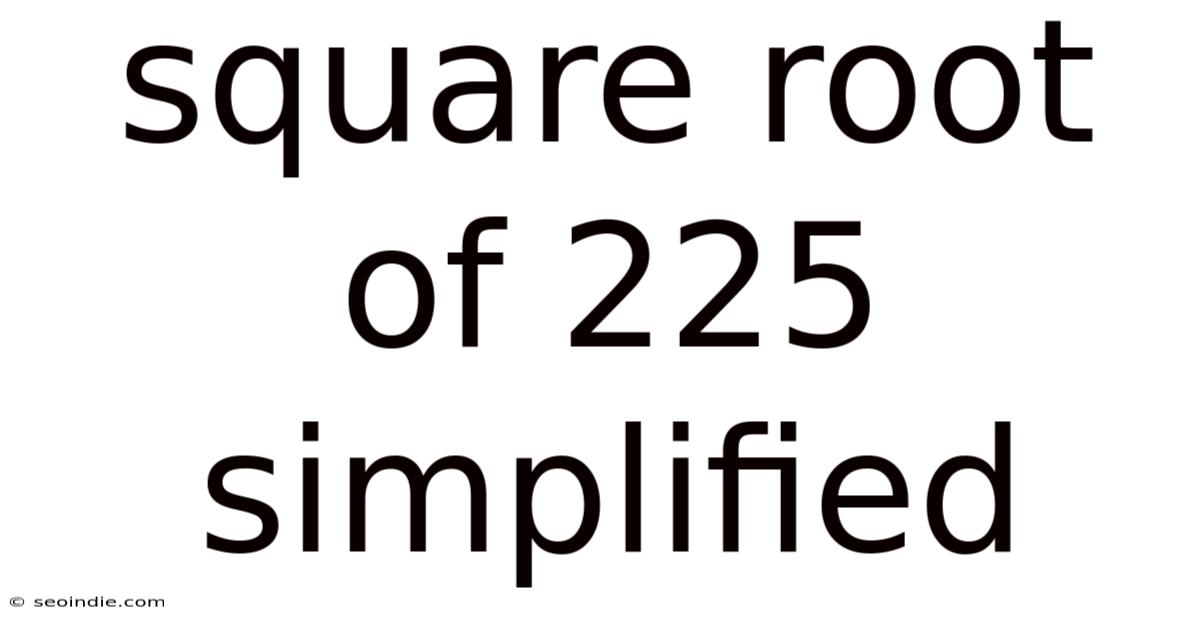
Table of Contents
Unveiling the Simplicity: Understanding the Square Root of 225
Finding the square root of a number might seem like a daunting task, especially for larger numbers. But what if the number is 225? This article will delve into the process of simplifying the square root of 225, exploring not only the solution but also the underlying mathematical concepts and practical applications. We'll unravel the mystery behind this seemingly complex calculation, breaking it down into manageable steps and providing a deeper understanding of square roots in general. By the end, you'll not only know the answer but also possess a solid grasp of the methods used to arrive at it.
Understanding Square Roots
Before we tackle the square root of 225, let's establish a fundamental understanding of what a square root actually is. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 * 3 = 9. Similarly, the square root of 16 is 4 because 4 * 4 = 16. This concept is represented mathematically as √x, where 'x' is the number whose square root we are seeking.
The square root of 225, denoted as √225, is the number that, when multiplied by itself, equals 225. This number is a whole number, making it a relatively straightforward calculation compared to finding the square root of numbers that don't result in a perfect square.
Methods for Finding the Square Root of 225
There are several approaches to finding the square root of 225. Let's explore the most common and efficient methods:
1. Prime Factorization
Prime factorization is a powerful technique for simplifying square roots, especially for larger numbers. It involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This method is particularly useful when dealing with numbers that have perfect square factors.
Let's apply prime factorization to 225:
- Step 1: Find a prime factor. We can start by dividing 225 by the smallest prime number, 3. 225 / 3 = 75.
- Step 2: Continue the process. Now, we have 75. We can divide 75 by 3 again, resulting in 25.
- Step 3: Find the next prime factor. 25 is divisible by 5, giving us 5.
- Step 4: Identify all prime factors. 5 is a prime number. Therefore, the prime factorization of 225 is 3 x 3 x 5 x 5, or 3² x 5².
Now, let's use this factorization to simplify the square root:
√225 = √(3² x 5²) = √3² x √5² = 3 x 5 = 15
Therefore, the square root of 225 is 15.
2. Using a Calculator
In today's digital age, using a calculator is a quick and efficient way to find the square root of any number. Simply enter 225 and press the square root button (√). The calculator will instantly display the answer, 15. While this method is convenient, understanding the underlying mathematical principles remains crucial for a deeper comprehension.
3. Estimation and Trial and Error
For smaller numbers, estimation and trial and error can be a helpful approach. You can start by estimating the square root and then refine your guess by squaring your estimate and comparing it to the original number. For example, we know that 10² = 100 and 20² = 400. Since 225 lies between 100 and 400, its square root must be between 10 and 20. Further trials might lead you to discover that 15² = 225. This method is less efficient for larger numbers but provides valuable intuition about square roots.
Perfect Squares and Their Significance
The number 225 is a perfect square because its square root is a whole number (15). Perfect squares are numbers that can be obtained by squaring a whole number. They are integral to understanding quadratic equations, geometry, and many other mathematical concepts. Recognizing perfect squares can significantly simplify calculations and problem-solving in various areas. Understanding perfect squares helps in quickly calculating the square roots of specific numbers and facilitates more efficient solutions in different applications.
Applications of Square Roots
The concept of square roots extends far beyond simple mathematical exercises. It has numerous applications in various fields:
- Geometry: Calculating the diagonal of a square or rectangle uses the Pythagorean theorem, which fundamentally involves square roots. Determining the distance between two points on a coordinate plane also necessitates the use of square roots.
- Physics: Many physics formulas involve square roots, particularly those related to calculating velocity, acceleration, and energy.
- Engineering: Engineers use square roots extensively in structural calculations, designing bridges, buildings, and other infrastructure.
- Statistics: Standard deviation, a key concept in statistics, is calculated using the square root of variance, a measure of data dispersion.
- Computer Science: Square roots are utilized in various algorithms and computations related to graphics, animation, and game development.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a square and a square root?
A square is the result of multiplying a number by itself (e.g., 15² = 225). A square root is the number that, when multiplied by itself, gives the original number (e.g., √225 = 15). They are inverse operations of each other.
Q2: Are there negative square roots?
While we typically focus on the principal square root (the positive value), every positive number has two square roots: one positive and one negative. For example, both 15 and -15, when squared, result in 225. However, when we write √225, we generally mean the positive square root, 15.
Q3: How do I simplify other square roots?
To simplify other square roots, use prime factorization to identify perfect square factors within the radicand (the number inside the square root symbol). Extract the perfect square factors as their square roots and leave the remaining factors inside the square root.
Q4: Can I simplify the square root of a negative number?
The square root of a negative number involves imaginary numbers, represented by the symbol 'i', where i² = -1. This topic falls under the realm of complex numbers and is beyond the scope of this article focused on simplifying the square root of 225.
Q5: Why is understanding square roots important?
Understanding square roots is fundamental to grasping many mathematical concepts, from geometry and algebra to calculus and advanced mathematical applications in various fields like physics, engineering, and computer science. It's a foundational concept that forms the basis for numerous more complex calculations and problem-solving techniques.
Conclusion
Simplifying the square root of 225, as we've demonstrated, can be approached through different methods, each providing valuable insights into mathematical principles. From prime factorization to using a calculator, the process is relatively straightforward because 225 is a perfect square. However, the underlying concepts extend far beyond this specific example. Understanding square roots is a crucial foundation for various mathematical concepts and applications across numerous fields. This exploration not only provides the solution (15) but also enhances your understanding of square roots, their properties, and their significance in the broader mathematical landscape. By grasping these concepts, you've taken a significant step towards mastering a fundamental aspect of mathematics.
Latest Posts
Latest Posts
-
How To Find Kinetic Friction
Sep 21, 2025
-
Lenovo 7 Inch Tablet Byjus
Sep 21, 2025
-
Are Integers Closed Under Multiplication
Sep 21, 2025
-
What Equals 28 In Multiplication
Sep 21, 2025
-
How To Draw A Octagon
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 225 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.