Square Root Of 180 Simplified
seoindie
Sep 12, 2025 · 5 min read
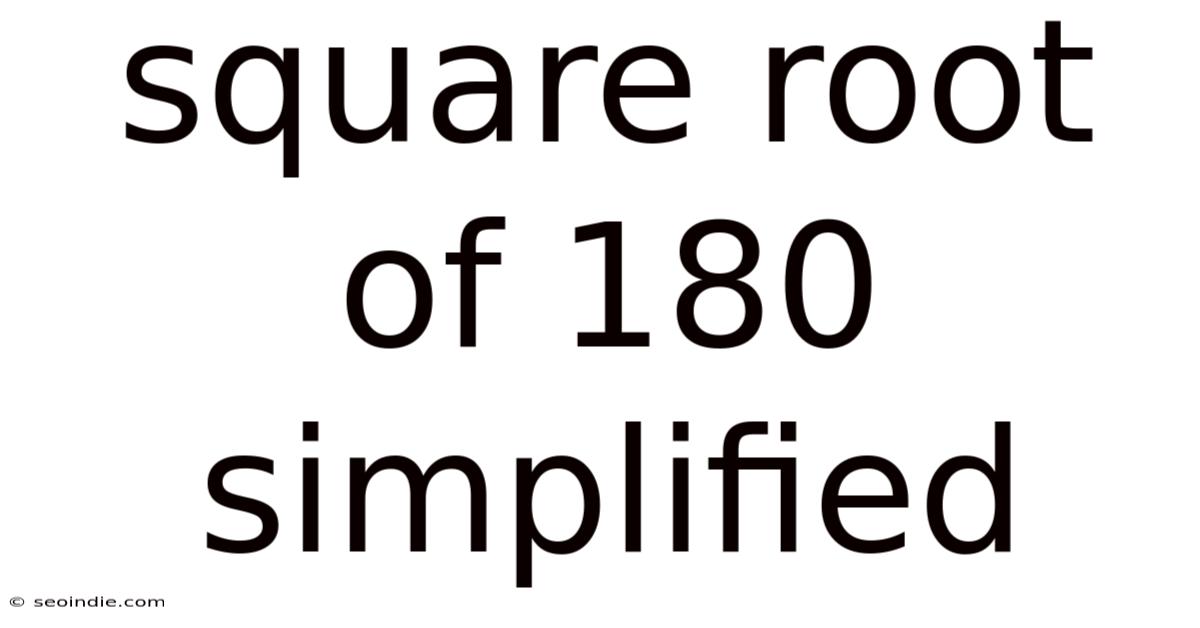
Table of Contents
Unveiling the Simplicity: A Deep Dive into Simplifying the Square Root of 180
Finding the square root of a number isn't always straightforward. While some numbers have neat, whole-number square roots, many others, like the square root of 180, require a bit more work to simplify. This article will guide you through the process of simplifying √180, explaining the underlying mathematical principles, and providing a step-by-step approach you can apply to other similar problems. Understanding this process will solidify your grasp of radical simplification and prime factorization.
Understanding Square Roots and Prime Factorization
Before we tackle √180, let's refresh our understanding of fundamental concepts. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, many numbers don't have such neat whole-number square roots. This is where simplification comes in.
Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This technique is crucial for simplifying square roots. By finding the prime factors of a number, we can identify perfect squares hidden within, allowing us to simplify the radical expression.
Step-by-Step Simplification of √180
Let's break down the simplification of √180 into manageable steps:
1. Prime Factorization of 180:
The first step is to find the prime factorization of 180. We can do this using a factor tree:
- 180 is divisible by 2: 180 = 2 x 90
- 90 is divisible by 2: 90 = 2 x 45
- 45 is divisible by 3: 45 = 3 x 15
- 15 is divisible by 3: 15 = 3 x 5
- 5 is a prime number.
Therefore, the prime factorization of 180 is 2 x 2 x 3 x 3 x 5, or 2² x 3² x 5.
2. Identifying Perfect Squares:
Now, examine the prime factorization: 2² x 3² x 5. Notice that we have 2² and 3², which are perfect squares (2 x 2 = 4 and 3 x 3 = 9).
3. Rewriting the Square Root:
We can rewrite √180 using the prime factorization: √(2² x 3² x 5).
4. Applying the Product Rule for Radicals:
The product rule for radicals states that √(a x b) = √a x √b. Using this rule, we can separate the square root:
√(2² x 3² x 5) = √2² x √3² x √5
5. Simplifying Perfect Squares:
Since √2² = 2 and √3² = 3, we can simplify the expression:
2 x 3 x √5
6. Final Simplified Form:
Finally, we multiply the whole numbers together:
6√5
Therefore, the simplified form of √180 is 6√5.
A Deeper Dive into the Mathematics: Why This Works
The simplification process relies on the fundamental properties of square roots and prime factorization. Let's delve deeper into the mathematical reasoning behind each step:
-
Prime Factorization's Role: By breaking down 180 into its prime factors, we're effectively dissecting the number into its fundamental building blocks. This allows us to identify any perfect square factors hidden within the larger number. Without prime factorization, identifying these perfect squares would be significantly more challenging, if not impossible for larger numbers.
-
The Power of Perfect Squares: Perfect squares are crucial because their square roots are whole numbers. This allows us to remove them from under the radical sign, simplifying the expression. Any factor that isn't a perfect square remains under the radical.
-
Product Rule of Radicals: This rule is fundamental to simplifying radical expressions. It allows us to separate a radical containing a product into a product of separate radicals. This is a key step in isolating the perfect squares within the radical expression.
-
Why We Can't Simplify Further: The final simplified form is 6√5. We can't simplify this further because 5 is a prime number and doesn't contain any perfect square factors. The simplification process is complete when all perfect square factors have been removed from under the radical.
Applying the Method to Other Square Roots
The method used to simplify √180 can be applied to simplify any square root. Here's a general approach:
- Prime Factorize: Find the prime factorization of the number under the square root.
- Identify Perfect Squares: Look for pairs of identical prime factors. Each pair represents a perfect square.
- Rewrite using Product Rule: Rewrite the square root using the product rule, separating each perfect square.
- Simplify Perfect Squares: Take the square root of each perfect square, removing them from under the radical.
- Combine Remaining Factors: Multiply any remaining whole numbers outside the radical.
Frequently Asked Questions (FAQs)
Q: What if the number under the square root is negative?
A: The square root of a negative number is an imaginary number. The simplification process described here applies only to non-negative numbers. Imaginary numbers are represented using the imaginary unit "i," where i² = -1.
Q: Can I use a calculator to simplify square roots?
A: While a calculator can provide a decimal approximation of a square root, it won't necessarily give you the simplified radical form. The methods outlined in this article are essential for obtaining the simplified radical expression.
Q: Why is simplifying square roots important?
A: Simplifying square roots is crucial for several reasons:
- Accuracy: Simplified radical forms are often more accurate than decimal approximations, especially in mathematical calculations.
- Efficiency: Simplified expressions are easier to work with and manipulate in further algebraic calculations.
- Understanding: The simplification process reinforces the understanding of prime factorization, perfect squares, and the properties of radicals.
Conclusion
Simplifying the square root of 180, or any square root for that matter, is a systematic process that relies on prime factorization and the properties of radicals. By understanding these concepts and following the steps outlined, you can confidently simplify any square root and develop a stronger foundation in algebraic manipulation. Remember, practice is key to mastering this skill. Try simplifying other square roots using the techniques described here and gradually increase the complexity of the numbers you work with. The more you practice, the more intuitive and efficient this process will become. You’ll find yourself tackling even the most complex square roots with confidence and precision.
Latest Posts
Latest Posts
-
Are Virtual Images Always Upright
Sep 12, 2025
-
Words That End In Alt
Sep 12, 2025
-
Words With Root Word Photo
Sep 12, 2025
-
Strong Acids And Bases List
Sep 12, 2025
-
200cm Is How Many Feet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 180 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.