Square Root Of 13 Simplified
seoindie
Sep 25, 2025 · 5 min read
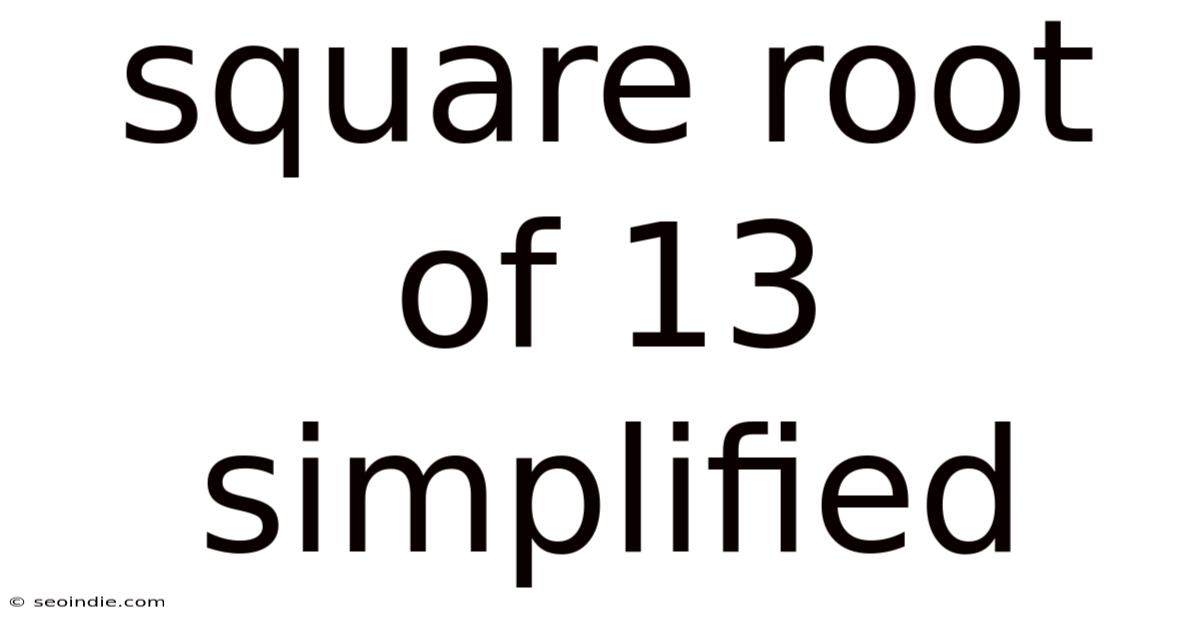
Table of Contents
Unveiling the Mysteries of the Square Root of 13: A Deep Dive into Simplification and Approximation
The square root of 13, denoted as √13, is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. Understanding how to simplify √13, even though it cannot be simplified in the same way as, say, √16 (which simplifies to 4), involves exploring its properties, approximating its value, and understanding its place within the broader context of number systems. This article will delve into these aspects, providing a comprehensive guide suitable for students and anyone interested in deepening their mathematical understanding.
Understanding Irrational Numbers and Simplification
Before tackling √13 specifically, let's clarify what "simplification" means in the context of square roots. When we simplify a square root, we aim to remove any perfect square factors from the radicand (the number inside the square root symbol). For example, √12 can be simplified because 12 contains a perfect square factor (4): √12 = √(4 x 3) = √4 x √3 = 2√3. This simplifies the expression, leaving only the irreducible square root, √3.
However, 13 is a prime number; it's only divisible by 1 and itself. It doesn't contain any perfect square factors other than 1. Therefore, √13 is already in its simplest radical form. We cannot simplify it further using this method. This doesn't mean it's not valuable or important to understand; it simply means its simplest form is itself.
Approximating the Value of √13
Since we cannot express √13 as a simple fraction or a terminating decimal, we often rely on approximations. Several methods exist to estimate its value:
1. Using a Calculator:
The most straightforward method is using a calculator. Most calculators will provide a decimal approximation of √13, typically around 3.60555. This is convenient for practical applications, but it doesn't offer insight into the underlying mathematical principles.
2. The Babylonian Method (or Heron's Method):
This iterative method provides increasingly accurate approximations. It's based on the principle that if x is an approximation of √n, then a better approximation is given by the average of x and n/x. Let's illustrate:
- Start with an initial guess: Let's guess 3.
- Apply the formula: (3 + 13/3) / 2 ≈ 3.6667
- Repeat the process: (3.6667 + 13/3.6667) / 2 ≈ 3.6056
- Continue iterating: Each iteration yields a more precise approximation. After a few iterations, the approximation converges to the actual value.
This method demonstrates how we can systematically refine our approximation without relying solely on a calculator.
3. Linear Approximation using Derivatives (Calculus Approach):
For those familiar with calculus, linear approximation using derivatives provides a powerful technique. We can approximate the function f(x) = √x near a known point. Let's use x = 9 (since √9 = 3 is easy to calculate):
- Find the derivative: f'(x) = 1/(2√x)
- Evaluate at x = 9: f'(9) = 1/(2√9) = 1/6
- Use the linear approximation formula: f(x) ≈ f(a) + f'(a)(x-a), where a = 9 and x = 13.
- Calculate: √13 ≈ √9 + (1/6)(13 - 9) = 3 + (1/6)(4) = 3 + 2/3 ≈ 3.6667
This method gives a relatively good approximation, though less precise than several iterations of the Babylonian method.
Visualizing √13 Geometrically
We can also visualize √13 geometrically. Consider a right-angled triangle with legs of length 2 and 3. By the Pythagorean theorem (a² + b² = c²), the hypotenuse (c) has length √(2² + 3²) = √(4 + 9) = √13. This provides a geometric interpretation of the square root – it represents the length of the hypotenuse.
√13 in Different Number Systems
While √13 is irrational in the real number system, its representation can differ in other number systems:
- Decimal System: As discussed, its decimal representation is a non-repeating, non-terminating decimal (approximately 3.60555...).
- Binary System: The binary representation is also infinite and non-repeating.
- Continued Fractions: √13 can be expressed as a continued fraction: 3 + 1/(1 + 1/(1 + 1/(1 + 1/(6 + ...)))) This representation provides a unique way to approximate the value.
Applications of √13
Although it might seem like a purely theoretical concept, √13 and other irrational numbers find applications in various fields:
- Physics: Calculations involving vectors, distances, and energy often involve irrational numbers.
- Engineering: Design and construction projects often require precise calculations that incorporate irrational numbers.
- Computer Graphics: Generating smooth curves and realistic images frequently uses irrational numbers in algorithms.
- Mathematics: √13 plays a role in number theory, particularly in the study of quadratic forms and Diophantine equations.
Frequently Asked Questions (FAQ)
-
Q: Is √13 a rational number? A: No, √13 is an irrational number. It cannot be expressed as a fraction of two integers.
-
Q: Can √13 be simplified further? A: No, √13 is already in its simplest form because 13 is a prime number and has no perfect square factors other than 1.
-
Q: What is the approximate value of √13? A: Approximately 3.60555. The exact value is non-terminating and non-repeating.
-
Q: What are some methods to approximate √13? A: Calculators, the Babylonian method, and linear approximation using derivatives are some methods.
-
Q: Why is understanding √13 important? A: Understanding irrational numbers like √13 is crucial for a solid foundation in mathematics and its applications in various scientific and engineering fields. It also helps us appreciate the richness and complexity of the number system.
Conclusion
The square root of 13, though seemingly simple, offers a gateway to understanding deeper concepts in mathematics. While it cannot be simplified in the traditional sense, its value can be approximated using various methods, each offering different insights into numerical analysis and approximation techniques. Its irrational nature highlights the vastness and complexity of the number system, reminding us that many numbers exist beyond simple fractions and terminating decimals. Appreciating its properties and applications broadens our mathematical horizons and strengthens our foundational understanding of numbers. From geometric visualizations to its role in advanced mathematical concepts, √13 serves as a valuable example of the intricacies and beauty inherent in mathematics.
Latest Posts
Latest Posts
-
No Objection Letter From Parents
Sep 25, 2025
-
Area Of A Kite Calculator
Sep 25, 2025
-
Plant With Small Pink Flowers
Sep 25, 2025
-
Gcf Of 26 And 39
Sep 25, 2025
-
Are Amoeba Heterotrophic Or Autotrophic
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 13 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.