Square Root Of 112 Simplified
seoindie
Sep 25, 2025 · 5 min read
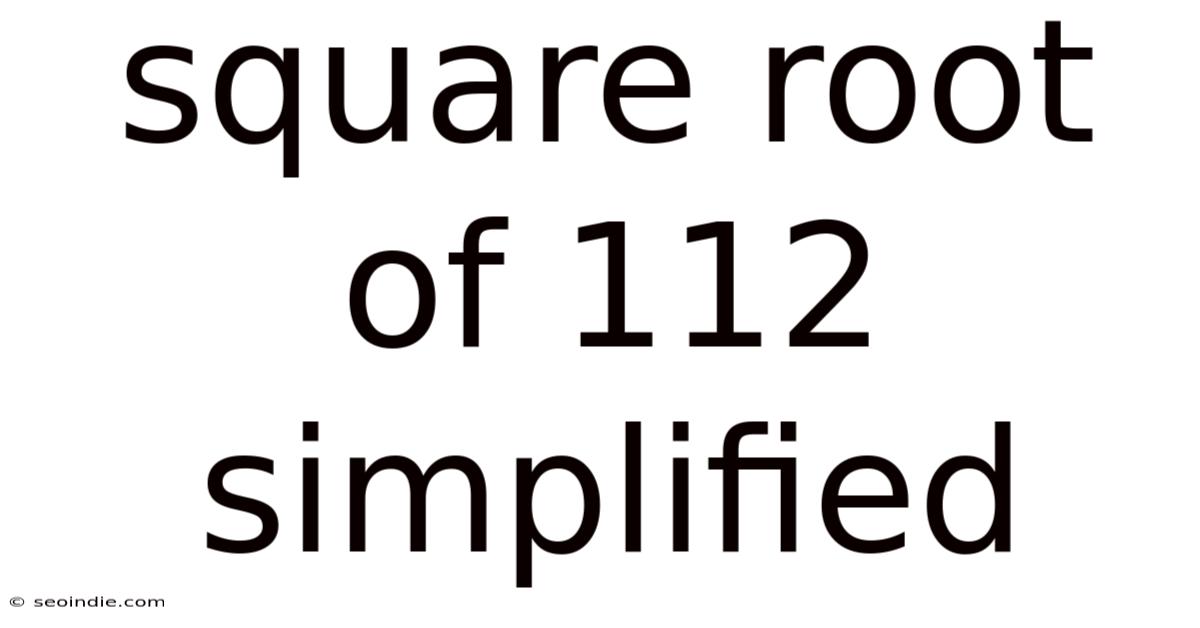
Table of Contents
Unveiling the Secrets of √112: A Comprehensive Guide to Simplifying Square Roots
Understanding how to simplify square roots is a fundamental skill in mathematics, crucial for algebra, calculus, and beyond. This comprehensive guide will walk you through the process of simplifying the square root of 112 (√112), explaining the underlying principles and offering practical steps to solve similar problems. We'll explore various methods, delve into the mathematical theory, and address frequently asked questions, ensuring you gain a deep understanding of this important concept. This guide is designed for students of all levels, from those just starting to learn about radicals to those looking to solidify their understanding.
Understanding Square Roots and Simplification
Before diving into √112, let's establish a solid foundation. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Not all numbers have perfect square roots (like 9, 16, 25, etc.). Numbers like 112 have irrational square roots, meaning their decimal representation goes on forever without repeating. This is why simplifying is important. Simplifying a square root means expressing it in its simplest radical form, removing any perfect square factors from under the radical symbol (√).
Method 1: Prime Factorization for Simplifying √112
The most reliable method for simplifying square roots involves prime factorization. This technique breaks down a number into its prime factors – numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's apply this to √112:
-
Find the prime factorization of 112:
We can start by dividing 112 by the smallest prime number, 2:
112 ÷ 2 = 56 56 ÷ 2 = 28 28 ÷ 2 = 14 14 ÷ 2 = 7
Therefore, the prime factorization of 112 is 2 x 2 x 2 x 2 x 7 = 2<sup>4</sup> x 7
-
Rewrite the square root using the prime factorization:
√112 = √(2<sup>4</sup> x 7)
-
Simplify the square root:
Remember that √(a x b) = √a x √b. We can simplify the square root of 2<sup>4</sup>:
√(2<sup>4</sup>) = 2<sup>4/2</sup> = 2<sup>2</sup> = 4
Therefore:
√112 = √(2<sup>4</sup> x 7) = √(2<sup>4</sup>) x √7 = 4√7
Therefore, the simplified form of √112 is 4√7.
Method 2: Identifying Perfect Square Factors
This method is a slightly faster alternative if you can quickly identify perfect square factors within the number. A perfect square is a number that is the square of an integer (e.g., 4, 9, 16, 25, 36...).
-
Identify perfect square factors of 112:
We know that 112 is divisible by 4 (112 ÷ 4 = 28), and 4 is a perfect square (2²). Also, 28 is divisible by 4 (28 ÷ 4 = 7).
-
Rewrite 112 using perfect square factors:
112 = 4 x 4 x 7 = 4² x 7
-
Simplify the square root:
√112 = √(4² x 7) = √(4²) x √7 = 4√7
This method arrives at the same simplified form, 4√7, but requires a bit more intuition in identifying perfect square factors.
A Deeper Dive into the Mathematical Principles
The simplification process hinges on the fundamental properties of square roots and exponents:
-
Product Property of Square Roots: √(a x b) = √a x √b This allows us to break down a complex square root into smaller, more manageable parts.
-
Quotient Property of Square Roots: √(a/b) = √a / √b This is useful for simplifying square roots involving fractions.
-
Exponent Rules: Understanding how exponents work is essential. Remember that √a = a<sup>1/2</sup>. This connection is crucial for understanding why we can simplify √(2<sup>4</sup>) to 2<sup>2</sup> (by dividing the exponent by 2).
Expanding the Concept: Simplifying Other Square Roots
The methods demonstrated with √112 are universally applicable. Let's try another example: simplify √75
-
Prime Factorization: 75 = 3 x 5 x 5 = 3 x 5²
-
Simplification: √75 = √(3 x 5²) = √3 x √5² = 5√3
Therefore, √75 simplifies to 5√3.
Frequently Asked Questions (FAQ)
- Q: Why is simplifying square roots important?
A: Simplifying square roots makes mathematical expressions easier to understand and work with. It helps in simplifying calculations and solving equations.
- Q: What if the number under the square root is negative?
A: The square root of a negative number involves imaginary numbers (denoted by 'i', where i² = -1). This is a more advanced topic in complex numbers.
- Q: Can I use a calculator to simplify square roots?
A: Calculators can provide decimal approximations of square roots, but they usually don't give the simplified radical form. The methods described above are crucial for obtaining the exact simplified form.
- Q: Are there any other methods for simplifying square roots?
A: While prime factorization and identifying perfect squares are the most common and reliable methods, other techniques exist, often involving recognizing patterns and using algebraic manipulations. However, these are generally less efficient than the methods described.
Conclusion: Mastering the Art of Square Root Simplification
Simplifying square roots is a fundamental mathematical skill with wide-ranging applications. By mastering the techniques of prime factorization and identifying perfect square factors, you can confidently tackle even the most complex square root simplification problems. Remember, the key is to break down the number into its prime factors or perfect square components and then extract the perfect squares from under the radical symbol. This guide provides a solid foundation for understanding and applying these crucial concepts. Practice is key – the more you work with these methods, the faster and more intuitive they will become. Remember to always double-check your work, ensuring your simplified radical is in its most concise form. With consistent practice and a solid understanding of the underlying mathematical principles, you'll become proficient in simplifying square roots, unlocking a deeper understanding of the world of mathematics.
Latest Posts
Latest Posts
-
Definition Of Fibrous Root System
Sep 25, 2025
-
A Pic Of A Hexagon
Sep 25, 2025
-
List The Factors Of 19
Sep 25, 2025
-
Pink And White Small Flowers
Sep 25, 2025
-
Most Popular Sports In Spain
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 112 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.