Square Root Of 100 Simplified
seoindie
Sep 18, 2025 · 6 min read
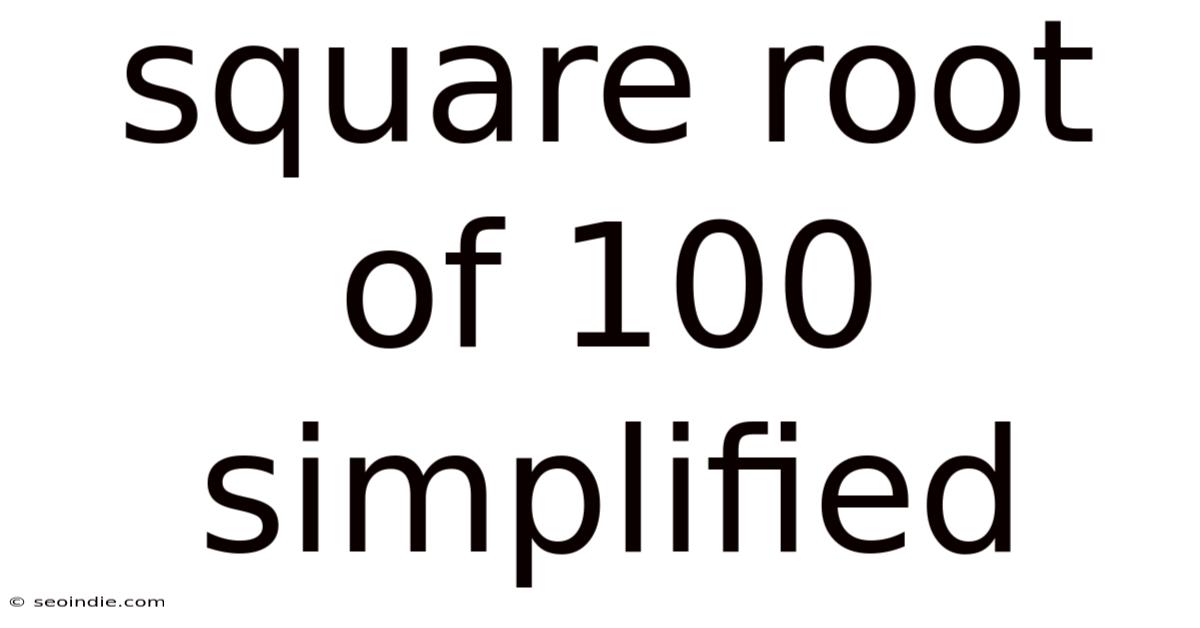
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 100 and Beyond
Finding the square root of 100 might seem like a simple task, a quick calculation for many. But delving deeper, we uncover a fascinating journey into the world of mathematics, revealing the fundamental concepts underpinning this seemingly straightforward operation and its broader implications within algebra, geometry, and beyond. This comprehensive guide will not only explain how to find the square root of 100 but also explore the underlying principles, provide practical examples, and answer frequently asked questions to solidify your understanding.
What is a Square Root?
Before we dive into the specifics of √100 (the square root of 100), let's establish a clear understanding of what a square root actually represents. A square root is a number that, when multiplied by itself, equals a given number. In simpler terms, it's the inverse operation of squaring a number. When we square a number (raise it to the power of 2), we multiply it by itself. For example, 5 squared (5²) is 5 x 5 = 25. Conversely, the square root of 25 (√25) is 5 because 5 x 5 = 25.
This concept can be visually represented using squares. If you imagine a square with sides of length 5 units, its area will be 5 x 5 = 25 square units. Therefore, the square root of the area (25 square units) gives you the length of one side (5 units). This geometric interpretation helps visualize the concept of square roots.
Calculating the Square Root of 100: The Simple Approach
Now, let's tackle the square root of 100. The question is: what number, when multiplied by itself, equals 100? The answer is relatively straightforward: 10. Because 10 x 10 = 100, the square root of 100 (√100) is 10.
This seemingly simple calculation lays the foundation for understanding more complex square root problems. The ability to quickly recognize perfect squares (numbers that are the result of squaring an integer) is crucial for efficient mathematical operations. Knowing that 100 is a perfect square (10²) allows for immediate calculation of its square root.
Beyond the Basics: Exploring Square Roots of Non-Perfect Squares
While finding the square root of a perfect square like 100 is easy, many numbers aren't perfect squares. For instance, what's the square root of 2? There isn't a whole number that, when multiplied by itself, equals 2. This is where the concept of irrational numbers comes into play. Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). The square root of 2 (√2) is an irrational number, approximately equal to 1.414.
Calculating the square root of non-perfect squares often requires using a calculator or applying numerical methods like the Babylonian method (also known as Heron's method), which involves iterative approximations to reach a closer and closer estimate of the square root.
The Square Root of 100 in Different Contexts
The concept of the square root of 100 extends beyond simple arithmetic. It plays a vital role in various mathematical areas, including:
-
Geometry: As mentioned earlier, the square root is essential in calculating lengths and areas of squares and other geometric figures. For example, if the area of a square is 100 square meters, the length of each side is √100 = 10 meters. This extends to more complex shapes and calculations involving Pythagoras' theorem, where the square root is used to find the lengths of sides in right-angled triangles.
-
Algebra: Square roots are fundamental to solving quadratic equations (equations of the form ax² + bx + c = 0). The quadratic formula, which provides solutions for these equations, directly involves the square root.
-
Physics: Many physical formulas incorporate square roots, particularly when dealing with concepts like velocity, acceleration, and energy.
-
Statistics: Standard deviation, a crucial measure of data dispersion, involves the square root.
Understanding the Principal Square Root
It's important to note that every positive number has two square roots: a positive one and a negative one. For example, both 10 and -10, when squared, result in 100 (10 x 10 = 100 and -10 x -10 = 100). However, when we talk about the square root of a number (denoted by √), we usually refer to the principal square root, which is the non-negative square root. Therefore, √100 = 10, not -10.
The concept of principal square root is critical for consistency and avoiding ambiguity in mathematical calculations.
Practical Applications and Real-World Examples
The application of square roots is widespread in everyday life, though often unnoticed. Here are a few examples:
-
Construction and Engineering: Calculating the dimensions of structures, determining the length of diagonals, and ensuring stability frequently involve square root calculations.
-
Computer Graphics and Game Development: Generating and manipulating images and 3D models often uses square root calculations for determining distances and positions.
-
Finance: Calculating investment returns, compound interest, and analyzing financial data often involves the use of square roots.
-
Navigation: Determining distances and locations using GPS technology relies heavily on mathematical functions, including square roots.
Frequently Asked Questions (FAQ)
Q1: What if I need to find the square root of a negative number?
A1: The square root of a negative number involves imaginary numbers, denoted by the symbol i, where i² = -1. For example, √-1 = i, and √-100 = 10i. Imaginary numbers are a separate branch of mathematics, extending the number system beyond real numbers.
Q2: Are there any shortcuts for calculating square roots?
A2: While calculators provide the most convenient method, recognizing perfect squares can significantly speed up calculations. Familiarity with the squares of integers (1, 4, 9, 16, 25, etc.) is crucial. Additionally, understanding the properties of square roots (like √(ab) = √a * √b) can simplify some calculations.
Q3: How can I improve my understanding of square roots?
A3: Practice is key! Solve various problems involving square roots, gradually increasing the complexity. Explore online resources, tutorials, and educational videos to enhance your understanding. Visual aids, such as geometric representations, can also improve comprehension.
Q4: What are some common mistakes to avoid when working with square roots?
A4: One common error is incorrectly simplifying square roots, especially those involving variables. Always ensure you understand the rules of exponents and radicals before simplifying expressions. Another mistake is forgetting the possibility of both positive and negative square roots, unless the principal square root is specifically requested.
Conclusion: Embracing the Power of Square Roots
The seemingly simple calculation of the square root of 100 opens a door to a vast and fascinating world of mathematical concepts and applications. Understanding the underlying principles, extending your knowledge to include irrational and imaginary numbers, and appreciating the diverse applications of square roots will empower you to approach more complex mathematical challenges with confidence. This journey beyond the simple arithmetic demonstrates that even seemingly basic mathematical operations offer rich opportunities for learning and exploration. The square root of 100 is not just 10; it's a gateway to deeper mathematical understanding and a key to unlocking numerous real-world problems.
Latest Posts
Latest Posts
-
Descriptive Words Starting With D
Sep 18, 2025
-
Adjective That Start With Y
Sep 18, 2025
-
Oxygen Number Of Valence Electrons
Sep 18, 2025
-
We Could Definitely Do That
Sep 18, 2025
-
What Is On A Globe
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 100 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.