Solve 4x 2 25 0
seoindie
Sep 19, 2025 · 5 min read
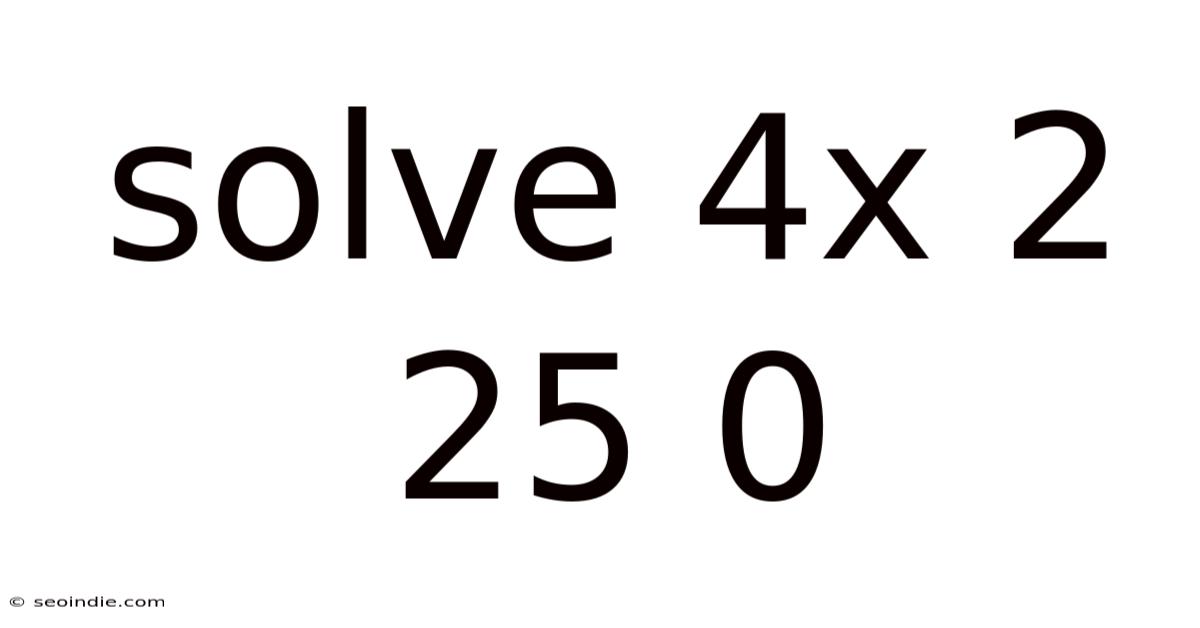
Table of Contents
Solving the Quadratic Equation: 4x² + 25 = 0
This article delves into the solution of the quadratic equation 4x² + 25 = 0. We'll explore various methods to solve this specific equation and then generalize the approach to tackle similar quadratic equations. Understanding quadratic equations is fundamental in algebra and has wide-ranging applications in various fields, from physics and engineering to finance and computer science. This comprehensive guide will equip you with the knowledge and skills to confidently solve such equations.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (if a=0, it becomes a linear equation). Our specific equation, 4x² + 25 = 0, is a quadratic equation where a = 4, b = 0, and c = 25. Notice the absence of the 'bx' term; this simplifies the solution process somewhat.
Method 1: Solving by Isolation
Since our equation lacks the 'bx' term, the simplest method is to isolate x². Let's walk through the steps:
-
Subtract 25 from both sides: This gives us 4x² = -25.
-
Divide both sides by 4: This simplifies the equation to x² = -25/4.
-
Take the square root of both sides: Remember that when taking the square root, we must consider both positive and negative solutions. Therefore, we get x = ±√(-25/4).
-
Simplify the square root: Since we have a negative number under the square root, we'll involve imaginary numbers. The square root of -1 is denoted by 'i' (the imaginary unit). We can rewrite the equation as: x = ±(√25/√4) * i = ±(5/2)i.
Therefore, the solutions to the equation 4x² + 25 = 0 are x = (5/2)i and x = -(5/2)i. These are complex conjugate solutions.
Method 2: Using the Quadratic Formula
The quadratic formula is a universal tool for solving any quadratic equation. It provides the solutions for the general equation ax² + bx + c = 0 as:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this to our equation: 4x² + 25 = 0. Here, a = 4, b = 0, and c = 25. Substituting these values into the quadratic formula:
x = [0 ± √(0² - 4 * 4 * 25)] / (2 * 4)
x = [± √(-400)] / 8
x = [± √(400) * i] / 8 (Since we have a negative number under the square root)
x = [± 20i] / 8
x = ±(20/8)i = ±(5/2)i
Again, we arrive at the same solutions: x = (5/2)i and x = -(5/2)i.
Understanding Complex Numbers
The solutions we obtained are complex numbers. A complex number has two parts: a real part and an imaginary part. They are generally written in the form a + bi, where 'a' is the real part and 'b' is the imaginary part. In our case, the real part is 0, and the imaginary part is ±(5/2). Complex numbers are essential in various branches of mathematics and its applications, especially in areas involving oscillations and waves.
Graphical Representation
While we can't directly plot complex numbers on a standard x-y plane (representing real numbers), we can visualize them using a complex plane (also known as an Argand diagram). The horizontal axis represents the real part, and the vertical axis represents the imaginary part. The points (0, 5/2) and (0, -5/2) would represent the solutions (5/2)i and -(5/2)i respectively on the complex plane.
Method 3: Factoring (Not Applicable in this Case)
Factoring is a method used to solve quadratic equations by expressing the quadratic as a product of two linear factors. However, this method is not directly applicable to our equation, 4x² + 25 = 0, because it doesn't factor nicely using real numbers. The expression 4x² + 25 is a sum of squares, and sums of squares cannot be factored using real numbers. Factoring becomes possible only when considering complex numbers.
Generalization and Application
The methods used to solve 4x² + 25 = 0 can be extended to solve other quadratic equations. The choice of method depends on the specific equation:
- Isolation: Useful when the 'bx' term is absent.
- Quadratic Formula: A universally applicable method for all quadratic equations.
- Factoring: Efficient when the quadratic expression factors easily.
Quadratic equations have numerous applications in various fields. For example:
- Physics: Describing projectile motion, the trajectory of a ball or other objects under the influence of gravity.
- Engineering: Analyzing stresses and strains in structures, designing electrical circuits.
- Finance: Modeling growth and decay, calculating compound interest.
- Computer Science: Algorithms and optimization problems.
Frequently Asked Questions (FAQ)
Q: What is an imaginary number?
A: An imaginary number is a number that, when squared, gives a negative result. It's defined using the imaginary unit 'i', where i² = -1.
Q: Why are the solutions complex conjugates?
A: Complex conjugate pairs frequently arise when solving quadratic equations with real coefficients but no real roots. The conjugate of a complex number a + bi is a - bi.
Q: Can I use a calculator to solve this equation?
A: While a standard calculator might not directly handle complex numbers, scientific or graphing calculators can handle complex number calculations. Alternatively, you can use online calculators specifically designed for solving quadratic equations.
Q: What if the equation had a 'bx' term?
A: If there were a 'bx' term (e.g., 4x² + 6x + 25 = 0), the quadratic formula would be the most straightforward method to find the solutions. Isolation and factoring would be less efficient or impossible.
Conclusion
Solving the quadratic equation 4x² + 25 = 0 involves understanding the concept of complex numbers and applying appropriate techniques like isolation or the quadratic formula. The solutions, (5/2)i and -(5/2)i, are complex conjugates, a common occurrence when solving quadratic equations without real roots. Mastering the solution of quadratic equations is a crucial step in developing a strong foundation in algebra and its applications across various disciplines. The ability to solve these equations efficiently and accurately opens doors to more complex mathematical challenges and problem-solving in many fields. Remember to always check your solutions by substituting them back into the original equation to verify their accuracy.
Latest Posts
Latest Posts
-
6 Letter Word Starting F
Sep 19, 2025
-
How Many Inches In 90cm
Sep 19, 2025
-
5 Cm How Many Meters
Sep 19, 2025
-
Is Salt A Homogeneous Mixture
Sep 19, 2025
-
Lcm Of 5 3 4
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Solve 4x 2 25 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.