Sin A - Sin B
seoindie
Sep 12, 2025 · 6 min read
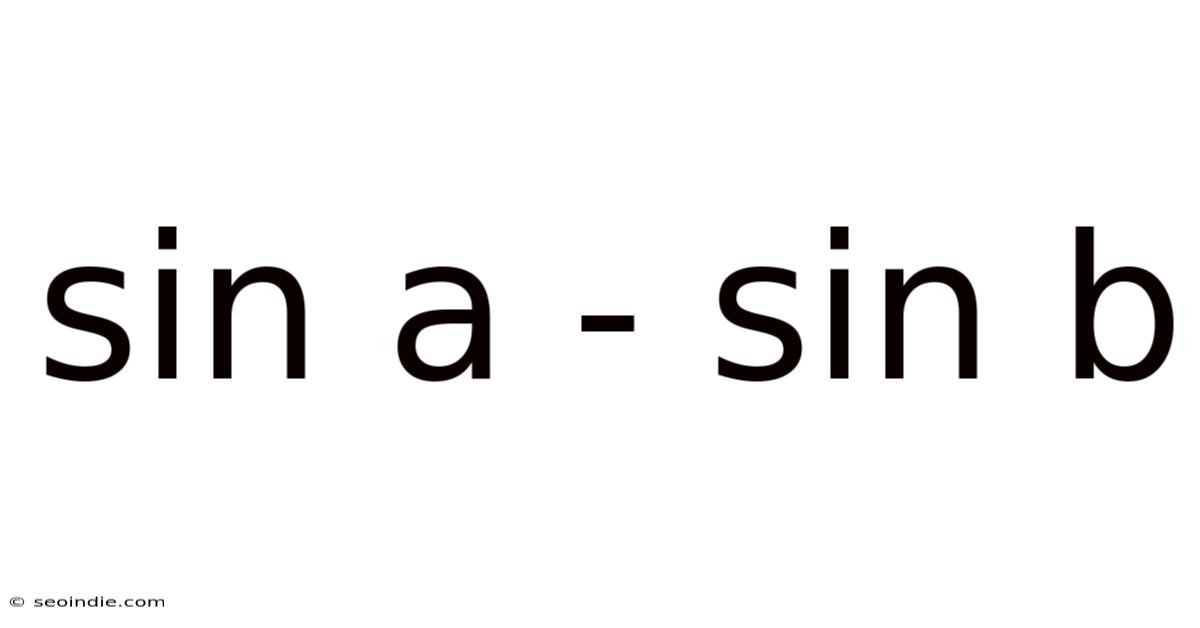
Table of Contents
Unraveling the Mystery: Sin A - Sin B
Understanding trigonometric identities is crucial for anyone navigating the world of mathematics, physics, and engineering. Among these identities, the difference of sines – sin A - sin B – often presents a challenge. This comprehensive guide will not only explain how to solve expressions involving sin A - sin B but also delve into its applications and provide a deeper understanding of its underlying principles. We’ll explore different approaches, from simple factorization to more advanced techniques, ensuring a firm grasp of this trigonometric concept for readers of all levels.
Introduction: A Deep Dive into Trigonometric Differences
The expression sin A - sin B, seemingly simple at first glance, holds significant importance in various mathematical and scientific fields. Mastering its manipulation unlocks the ability to solve complex equations, simplify intricate expressions, and gain a deeper understanding of wave phenomena and oscillatory systems. This article aims to provide a complete guide to this identity, offering multiple methods of solving problems and addressing frequently asked questions. We'll move from basic algebraic manipulation to employing the sum-to-product identities, ensuring a thorough understanding.
Understanding the Product-to-Sum Identities: The Foundation
Before tackling the direct simplification of sin A - sin B, it’s essential to understand the related product-to-sum identities. These identities provide the framework for transforming expressions involving products of trigonometric functions into sums or differences. These identities are derived from the angle sum and difference formulas for sine and cosine. They are:
- sin A + sin B = 2sin[(A+B)/2]cos[(A-B)/2]
- sin A - sin B = 2cos[(A+B)/2]sin[(A-B)/2]
- cos A + cos B = 2cos[(A+B)/2]cos[(A-B)/2]
- cos A - cos B = -2sin[(A+B)/2]sin[(A-B)/2]
The second identity listed above, sin A - sin B = 2cos[(A+B)/2]sin[(A-B)/2], is the key to simplifying expressions involving the difference of two sine functions. This identity allows us to express the difference as a product of cosine and sine functions, often leading to a more manageable form.
Method 1: Direct Application of the Sum-to-Product Identity
The most straightforward method for simplifying sin A - sin B is the direct application of the sum-to-product identity mentioned above:
sin A - sin B = 2cos[(A+B)/2]sin[(A-B)/2]
This identity transforms the difference of two sines into a product of a cosine and a sine term. The arguments of these trigonometric functions are the average and the half-difference of the original angles A and B. This is incredibly useful for simplifying equations and solving problems where the original form is less tractable.
Example: Simplify sin(3x) - sin(x).
Using the identity, we get:
sin(3x) - sin(x) = 2cos[(3x+x)/2]sin[(3x-x)/2] = 2cos(2x)sin(x)
This simplified expression is often easier to work with, especially in calculus or differential equations, where further manipulations might be necessary.
Method 2: Geometric Interpretation: The Unit Circle
A deeper understanding of sin A - sin B can be gained through its geometric interpretation on the unit circle. Consider two angles A and B on the unit circle. The sine of an angle represents the y-coordinate of the point where the terminal side of the angle intersects the unit circle. Therefore, sin A - sin B represents the difference in the y-coordinates of these two points. While this doesn't directly provide a simplified expression, it offers valuable insight into the nature of the difference and its relationship to the angles involved. Visualizing this difference on the unit circle can be incredibly helpful in understanding the behavior of the expression under different conditions.
Method 3: Using Complex Exponentials (Euler's Formula)
A more advanced approach involves using Euler's formula, which links trigonometric functions to complex exponentials:
e^(ix) = cos(x) + i sin(x)
By expressing sine functions as complex exponentials, we can manipulate the expression algebraically. While this method might seem more complex initially, it offers a powerful tool for solving more intricate trigonometric problems and is frequently utilized in advanced mathematical contexts. The manipulation of complex exponentials can sometimes lead to simplified forms that are not immediately apparent using purely trigonometric methods. This method requires a strong understanding of complex numbers and their properties.
Applications of Sin A - Sin B
The ability to simplify and manipulate sin A - sin B has numerous applications in various fields:
-
Solving Trigonometric Equations: The sum-to-product identities, especially the one for sin A - sin B, are essential tools for solving trigonometric equations. Transforming a difference into a product often allows for factorization and easier solution finding.
-
Signal Processing: In signal processing, the difference of sine waves represents the interference or beat phenomenon between two signals. Understanding the simplification of sin A - sin B allows for analysis and manipulation of these signals.
-
Physics: In physics, oscillatory systems are often modeled using sine and cosine functions. The difference of sine functions frequently appears in analyzing the superposition of waves and determining resultant amplitudes.
-
Calculus: Derivatives and integrals involving trigonometric functions often require the simplification techniques discussed here to obtain manageable expressions. The ability to convert a difference into a product can significantly simplify integration problems.
Frequently Asked Questions (FAQ)
-
Q: Can sin A - sin B be simplified further beyond the product form?
- A: The simplification to 2cos[(A+B)/2]sin[(A-B)/2] is generally the most concise and useful form. Further simplification depends on the specific values of A and B.
-
Q: What if A and B are equal?
- A: If A = B, then sin A - sin B = 0. This is directly evident from the original expression.
-
Q: How can I remember the sum-to-product identities?
- A: Repeated practice and the use of mnemonic devices can help. Understanding the derivation from the angle sum and difference formulas aids in recalling these identities.
-
Q: Are there similar identities for other trigonometric functions?
- A: Yes, similar sum-to-product and product-to-sum identities exist for cosine and tangent functions. These identities are equally crucial in simplifying complex trigonometric expressions.
Conclusion: Mastering the Difference
Mastering the simplification of sin A - sin B is a significant step towards a deeper understanding of trigonometry. By understanding the sum-to-product identity and its derivation, along with its geometric interpretation and applications, one can confidently tackle complex problems across various disciplines. The methods outlined here—direct application of the identity, geometric visualization, and the use of complex exponentials—offer a multifaceted approach, enabling a firm grasp of this essential trigonometric concept. Remember, consistent practice and a thorough understanding of the underlying principles are key to mastering this and other trigonometric identities. The more you work with these identities, the more intuitive their application will become.
Latest Posts
Latest Posts
-
The Square Root Of 8
Sep 12, 2025
-
Lcm For 10 And 15
Sep 12, 2025
-
What Is The Activity Series
Sep 12, 2025
-
List All Factors Of 32
Sep 12, 2025
-
Ingredients Of Milk Of Magnesia
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Sin A - Sin B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.