Π 5 Radians To Degrees
seoindie
Sep 12, 2025 · 5 min read
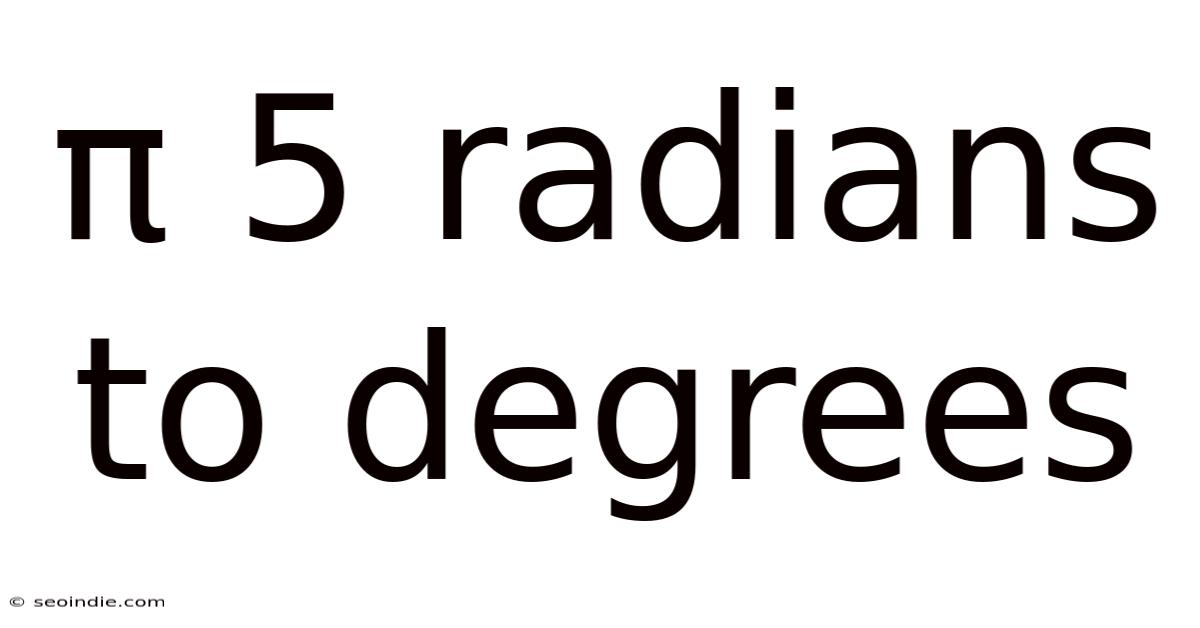
Table of Contents
Understanding π/5 Radians: A Comprehensive Guide to Radian-Degree Conversion
Pi (π) is a fundamental constant in mathematics, representing the ratio of a circle's circumference to its diameter. Understanding radians and how they relate to degrees is crucial in trigonometry, calculus, and many areas of physics and engineering. This article delves into the conversion of π/5 radians to degrees, providing a step-by-step explanation, exploring the underlying principles, and answering frequently asked questions. We will not only calculate the conversion but also solidify your understanding of the relationship between radians and degrees.
Introduction: Radians and Degrees – A Tale of Two Measures
Angles can be measured in two primary units: degrees and radians. Degrees, a familiar system, divides a circle into 360 equal parts. Radians, however, are based on the radius of the circle. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius. This seemingly more abstract system offers significant advantages in calculus and other advanced mathematical contexts because of its direct relationship to arc length and the circle's radius.
The conversion factor between radians and degrees stems from the fact that the total angle of a circle is 360 degrees or 2π radians. This fundamental relationship allows for seamless conversion between the two systems. Understanding this relationship is key to mastering many mathematical concepts.
Converting π/5 Radians to Degrees: A Step-by-Step Approach
To convert π/5 radians to degrees, we utilize the conversion factor:
- 180 degrees = π radians
This equation forms the basis of our conversion. We can rearrange this to solve for the conversion factor from radians to degrees:
- 1 radian = (180/π) degrees
Now, let's apply this to convert π/5 radians:
-
Substitute: Replace "1 radian" with "π/5 radians" in the conversion equation:
(π/5 radians) = (π/5) * (180/π) degrees
-
Simplify: Notice that 'π' cancels out from the numerator and denominator:
(π/5) * (180/π) degrees = (180/5) degrees
-
Calculate: Divide 180 by 5:
(180/5) degrees = 36 degrees
Therefore, π/5 radians is equal to 36 degrees. This is a relatively straightforward conversion, highlighting the elegance and efficiency of using the conversion factor based on the fundamental relationship between radians and degrees.
A Deeper Dive into the Geometry: Visualizing the Conversion
Imagine a circle with radius r. The circumference of this circle is 2πr. One radian subtends an arc of length r. Since the circumference contains 2π radians, it follows that 2π radians corresponds to 360 degrees.
Now, consider the angle π/5 radians. This represents (π/5) / (2π) = 1/10 of the total angle of a circle measured in radians. Since a full circle is 360 degrees, π/5 radians corresponds to (1/10) * 360 degrees = 36 degrees. This geometrical interpretation reinforces the mathematical conversion we performed earlier.
Applications of Radian Measure: Why Radians are Important
While degrees are intuitive for everyday angle measurements, radians possess distinct advantages in advanced mathematics and physics. Here's why:
-
Calculus: Radian measure simplifies calculus significantly, particularly in the differentiation and integration of trigonometric functions. Derivatives and integrals of trigonometric functions expressed in radians have simpler forms than their degree counterparts. This greatly simplifies calculations and problem-solving.
-
Arc Length and Sector Area: Radians directly relate to the arc length (s) and sector area (A) of a circle. These relationships are expressed elegantly as:
- s = rθ (where θ is the angle in radians)
- A = (1/2)r²θ (where θ is the angle in radians)
These formulas are far simpler and more direct when using radians compared to degrees, making calculations involving arc length and sector area much easier.
-
Physics and Engineering: Many physical phenomena, particularly those involving circular motion, oscillatory systems, and wave phenomena, are most naturally expressed using radians. Formulas in physics related to angular velocity, angular acceleration, and rotational kinetic energy are simplified when using radians.
-
Advanced Mathematics: In fields like complex analysis and topology, radians are the preferred unit of angular measurement because of their mathematical properties.
Frequently Asked Questions (FAQ)
-
Q: Why are radians used instead of degrees in higher-level mathematics?
A: Radians simplify calculus significantly because the derivatives and integrals of trigonometric functions are much simpler when using radians. This eliminates the need for cumbersome conversion factors that would be required if degrees were used.
-
Q: Can I use a calculator to convert radians to degrees?
A: Yes, most scientific calculators have a built-in function for converting between radians and degrees. Look for options that typically involve a button labeled "RAD" or "DEG" to switch between the modes. You can input the radian value and then convert it to degrees directly.
-
Q: What is the significance of 2π radians?
A: 2π radians represents a full circle (360 degrees). This is the fundamental relationship used in converting between radians and degrees.
-
Q: Is there a way to visualize π/5 radians?
A: Imagine dividing a circle into ten equal sectors. Each sector would represent π/5 radians or 36 degrees. This visual representation helps to understand the magnitude of the angle.
Conclusion: Mastering Radian-Degree Conversion
The conversion of π/5 radians to 36 degrees demonstrates the core principle of converting between radian and degree measures. While degrees are commonly used for everyday applications, understanding radians is crucial for progressing in advanced mathematics, physics, and engineering. This article not only provided a step-by-step guide to the conversion but also explored the underlying reasons for using radians, emphasizing their importance and applications in various fields. Mastering this conversion is a fundamental step towards a deeper understanding of circular geometry and its role in broader mathematical and scientific contexts. By understanding the relationship between radians and degrees and their respective strengths, you can confidently navigate the world of angles and their applications.
Latest Posts
Latest Posts
-
W O L F Wolf
Sep 12, 2025
-
What Is Bi Convex Lens
Sep 12, 2025
-
What Is 3 10 In Decimal
Sep 12, 2025
-
Based On The Solubility Guidelines
Sep 12, 2025
-
How Long Is 7 Meters
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Π 5 Radians To Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.