One Fifth As A Percentage
seoindie
Sep 15, 2025 · 6 min read
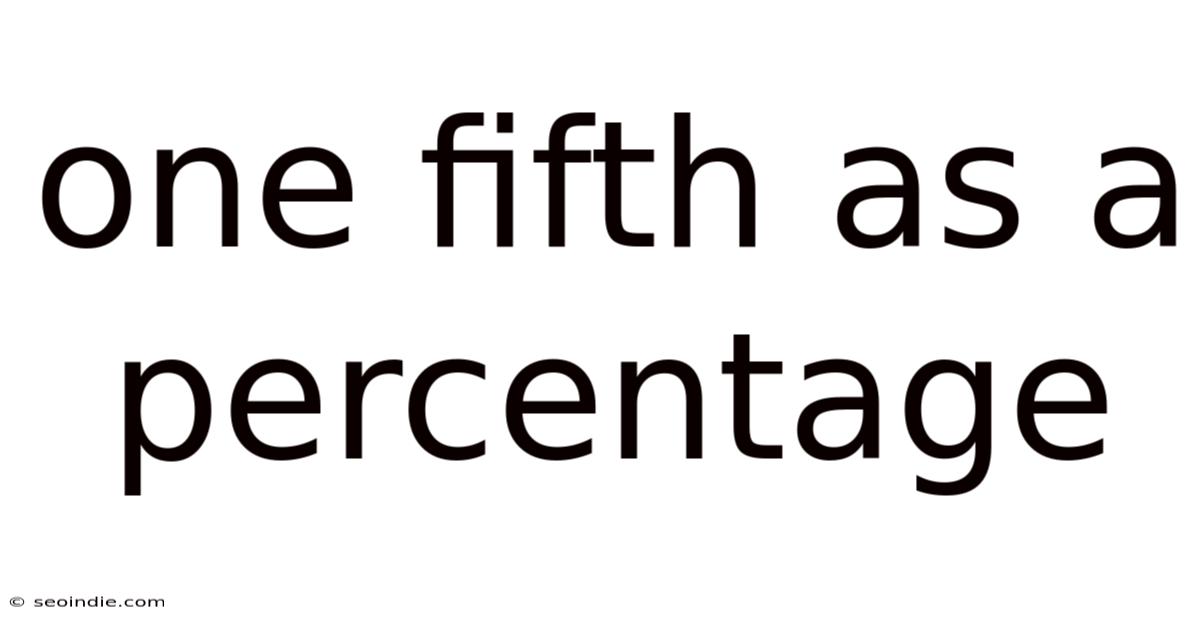
Table of Contents
One Fifth as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics and has widespread applications in everyday life, from calculating discounts to understanding financial reports. This article will delve deep into the concept of "one fifth as a percentage," explaining it in a clear, concise, and engaging manner, suitable for learners of all levels. We'll cover the conversion process, real-world examples, and frequently asked questions to solidify your understanding.
Introduction: Fractions, Decimals, and Percentages – A Triad
Before jumping into the specifics of one-fifth, let's refresh our understanding of the interconnectedness of fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction uses a numerator (top number) and a denominator (bottom number) to show the ratio of a part to the whole. A decimal expresses a fraction using base-10 notation, with a decimal point separating the whole number from the fractional part. A percentage represents a fraction or decimal as a portion of 100. Understanding this relationship is key to converting between these forms.
Converting One-Fifth to a Percentage: Step-by-Step
One-fifth, represented as 1/5, is a fraction indicating one part out of five equal parts. To convert this fraction to a percentage, we follow these simple steps:
-
Convert the Fraction to a Decimal: Divide the numerator (1) by the denominator (5): 1 ÷ 5 = 0.2
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.2 x 100 = 20%.
Therefore, one-fifth is equal to 20%.
Visualizing One-Fifth as a Percentage
Visual aids can greatly enhance understanding. Imagine a pie chart divided into five equal slices. One slice represents one-fifth of the whole pie. Since a whole pie represents 100%, one slice (one-fifth) represents 20% of the pie. This simple visualization makes the concept concrete and easy to grasp.
Real-World Applications of One-Fifth (20%)
The concept of one-fifth, or 20%, appears frequently in various real-world scenarios. Here are a few examples:
-
Discounts: A store offering a 20% discount on an item is essentially offering one-fifth off the original price. If an item costs $100, the discount would be $20 (1/5 of $100), resulting in a final price of $80.
-
Sales Commissions: A salesperson earning a 20% commission on sales earns one-fifth of the total sales value as their commission. If they sell $5000 worth of goods, their commission would be $1000.
-
Surveys and Statistics: In surveys and statistical analysis, 20% often represents a significant portion of the sample population. For instance, if 20% of respondents to a survey agree with a certain statement, it indicates a considerable level of agreement.
-
Financial Investments: Understanding percentages is crucial in financial planning and investment. A 20% return on investment represents a significant increase in the initial investment value.
Expanding on the Concept: Multiples of One-Fifth
Understanding one-fifth as 20% allows us to easily calculate multiples of one-fifth. For example:
-
Two-fifths: 2/5 = 2 x (1/5) = 2 x 20% = 40%
-
Three-fifths: 3/5 = 3 x (1/5) = 3 x 20% = 60%
-
Four-fifths: 4/5 = 4 x (1/5) = 4 x 20% = 80%
-
Five-fifths (the whole): 5/5 = 5 x (1/5) = 5 x 20% = 100%
Working with One-Fifth in Different Contexts
The application of one-fifth (20%) extends beyond simple percentage calculations. Let’s explore some more complex scenarios:
-
Calculating Percentage Increase or Decrease: Suppose the price of a product increases by one-fifth. This means the price increases by 20%. If the original price was $50, the increase would be $10 (20% of $50), resulting in a new price of $60. Similarly, a decrease of one-fifth represents a 20% reduction.
-
Proportionality Problems: One-fifth can be used to solve proportionality problems. For example, if 20% of a class of 25 students are absent, this means 5 students (one-fifth of 25) are absent.
-
Finding the Original Value from a Percentage: If you know that 20% of a number is 12, you can find the original number by setting up an equation: 0.2x = 12. Solving for x (the original number) gives x = 60.
The Mathematical Basis: Understanding the Conversion
The conversion from one-fifth to 20% fundamentally relies on the concept of proportionality. A percentage is simply a fraction expressed as a part of 100. To convert any fraction to a percentage, we find its equivalent fraction with a denominator of 100.
In the case of 1/5, we can find the equivalent fraction by multiplying both the numerator and denominator by 20: (1 x 20) / (5 x 20) = 20/100. This fraction, 20/100, directly translates to 20%. This method provides a strong mathematical foundation for understanding the conversion process.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate x% of y?
- A: To calculate x% of y, multiply y by (x/100). For example, to calculate 20% of 50, you would multiply 50 by (20/100) = 10.
-
Q: What is the difference between a fraction, a decimal, and a percentage?
- A: Fractions, decimals, and percentages are different ways of representing parts of a whole. Fractions use numerators and denominators, decimals use base-10 notation with a decimal point, and percentages represent a fraction or decimal as parts of 100.
-
Q: Can I convert any fraction to a percentage?
- A: Yes, any fraction can be converted to a percentage by dividing the numerator by the denominator and then multiplying by 100.
-
Q: Is there a shortcut for converting fractions with a denominator of 5 to percentages?
- A: Yes, since 1/5 is 20%, you can simply multiply the numerator by 20 to get the percentage equivalent.
-
Q: How do I convert a percentage back to a fraction?
- A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 20% becomes 20/100, which simplifies to 1/5.
Conclusion: Mastering the Concept of One-Fifth as a Percentage
Understanding one-fifth as 20% is a critical building block for mastering percentage calculations. By grasping the underlying principles, visualizing the concept, and applying it to real-world scenarios, you can confidently work with percentages in various contexts. Remember the simple steps involved in conversion and practice applying these techniques to improve your understanding and skills. The ability to seamlessly convert between fractions, decimals, and percentages is a highly valuable skill that will serve you well in numerous aspects of life. With consistent practice and application, you'll become proficient in working with percentages and confidently navigate numerical challenges involving fractions and their percentage equivalents.
Latest Posts
Latest Posts
-
Melting Point Periodic Table Trend
Sep 15, 2025
-
Questions About Acids And Bases
Sep 15, 2025
-
Hcl What Type Of Bond
Sep 15, 2025
-
Decimal Division Worksheet With Answers
Sep 15, 2025
-
Differentiate Between Evaporation And Vaporization
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about One Fifth As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.