Lcm Of 9 And 18
seoindie
Sep 17, 2025 · 6 min read
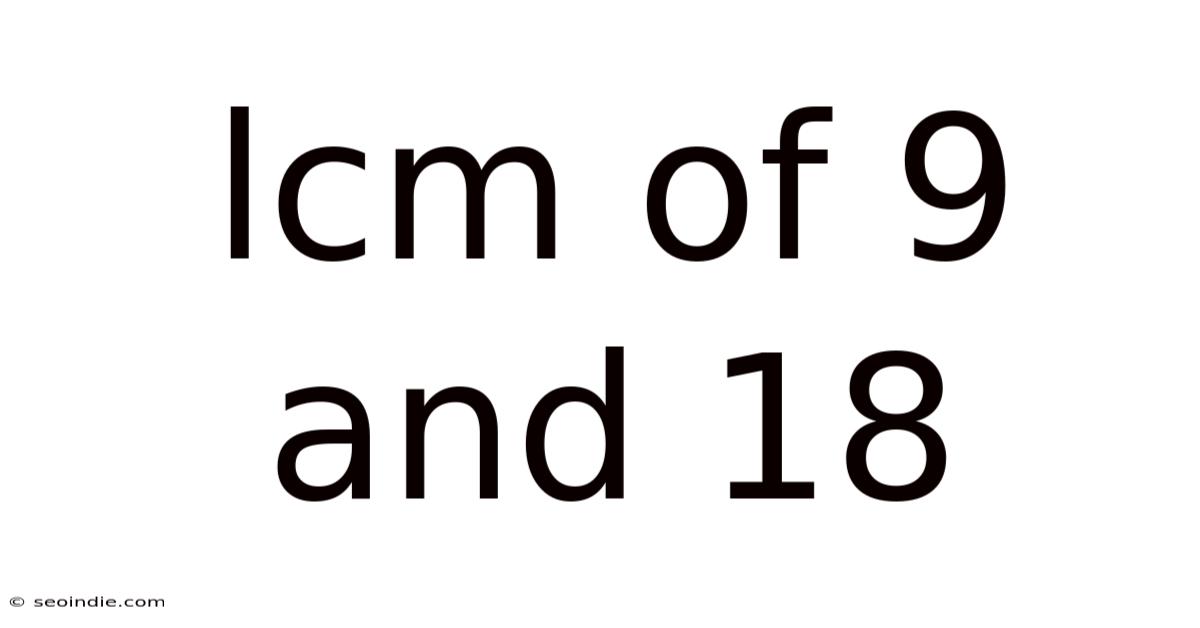
Table of Contents
Unveiling the Least Common Multiple (LCM) of 9 and 18: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple task, especially for smaller numbers like 9 and 18. However, understanding the underlying principles behind LCM calculations opens the door to a deeper appreciation of number theory and its applications in various fields, from scheduling to music theory. This comprehensive guide will not only show you how to calculate the LCM of 9 and 18 but will also delve into the methods, the underlying mathematics, and the broader significance of this concept.
Understanding Least Common Multiple (LCM)
Before we tackle the specific case of 9 and 18, let's establish a firm understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that both numbers divide into evenly without leaving a remainder. This concept is crucial in various mathematical and real-world applications, as we'll explore later.
Methods for Calculating LCM
There are several effective methods for determining the LCM of two numbers. Let's explore the most common approaches, illustrating each with the example of 9 and 18.
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54...
- Multiples of 18: 18, 36, 54, 72...
By comparing the lists, we quickly observe that the smallest common multiple is 18. Therefore, the LCM(9, 18) = 18. This method is intuitive but becomes less efficient when dealing with larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This approach is more systematic and efficient for larger numbers.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
To find the LCM, we identify the highest power of each prime factor present in either factorization and multiply them together:
LCM(9, 18) = 2 x 3² = 2 x 9 = 18
This method is more robust and scales well for larger numbers. It provides a deeper understanding of the number's structure and composition.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers themselves. This relationship is expressed as:
LCM(a, b) x GCD(a, b) = a x b
We can use this relationship to calculate the LCM if we know the GCD. Let's find the GCD of 9 and 18 using the Euclidean algorithm:
- Divide the larger number (18) by the smaller number (9): 18 ÷ 9 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number, which is 9.
Now, using the formula:
LCM(9, 18) = (9 x 18) / GCD(9, 18) = (9 x 18) / 9 = 18
This method highlights the interconnectedness between LCM and GCD, offering an alternative pathway to the solution.
Illustrative Examples: Expanding the Scope
Let's broaden our understanding by exploring LCM calculations with slightly more complex examples.
Example 1: LCM of 12 and 18
-
Listing Multiples:
- Multiples of 12: 12, 24, 36, 48...
- Multiples of 18: 18, 36, 54...
- LCM(12, 18) = 36
-
Prime Factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
- LCM(12, 18) = 2² x 3² = 4 x 9 = 36
-
GCD Method:
- GCD(12, 18) = 6 (using the Euclidean algorithm)
- LCM(12, 18) = (12 x 18) / 6 = 36
Example 2: LCM of 24 and 36
-
Listing Multiples: (becomes less practical with larger numbers)
-
Prime Factorization:
- 24 = 2³ x 3
- 36 = 2² x 3²
- LCM(24, 36) = 2³ x 3² = 8 x 9 = 72
-
GCD Method:
- GCD(24, 36) = 12
- LCM(24, 36) = (24 x 36) / 12 = 72
Real-World Applications of LCM
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical application in various scenarios:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. Finding the LCM of their arrival intervals helps determine when both buses will arrive simultaneously. This is crucial for optimizing schedules and coordinating transportation systems.
-
Music Theory: LCM plays a role in music theory, specifically in determining the least common multiple of the lengths of musical phrases or the frequency of beats, impacting the overall harmony and rhythm.
-
Construction and Engineering: In projects involving repetitive patterns or cycles, understanding LCM ensures efficient material usage and coordinated construction processes.
-
Computer Science: LCM is used in algorithms related to timing and synchronization in computer systems, particularly in concurrent programming.
Frequently Asked Questions (FAQ)
Q: Is the LCM always greater than or equal to the larger of the two numbers?
A: Yes, the LCM is always greater than or equal to the larger of the two numbers. This is because the LCM must be a multiple of both numbers.
Q: What if the two numbers are prime numbers?
A: If the two numbers are prime numbers (like 2 and 7), their LCM is simply their product (2 x 7 = 14). This is because prime numbers have only 1 and themselves as divisors, so they share no common factors other than 1. Their GCD is 1.
Q: Can we find the LCM of more than two numbers?
A: Yes, the LCM can be extended to more than two numbers. The prime factorization method is particularly useful for this, involving finding the highest power of each prime factor present in the factorization of all the numbers.
Conclusion: Beyond the Basics of LCM(9, 18)
While the calculation of the LCM of 9 and 18 might seem straightforward, the journey to understanding this concept unveils the elegance and power of number theory. Through various methods, we've not only calculated the LCM but also explored the deeper mathematical principles behind it. This understanding extends to a wide array of real-world applications, emphasizing the practical significance of this seemingly simple mathematical concept. The ability to efficiently calculate LCM is a fundamental skill that finds utility across numerous disciplines, proving its importance far beyond the classroom. Remember, understanding the why behind the calculation is just as important as knowing how to do it. This approach will empower you to tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Difference Between Amylopectin And Amylose
Sep 17, 2025
-
240 Sq Meters To Feet
Sep 17, 2025
-
Active Voice Worksheets With Answers
Sep 17, 2025
-
How Many 3 Number Combinations
Sep 17, 2025
-
All The Factors Of 91
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.