Lcm Of 9 And 15
seoindie
Sep 20, 2025 · 6 min read
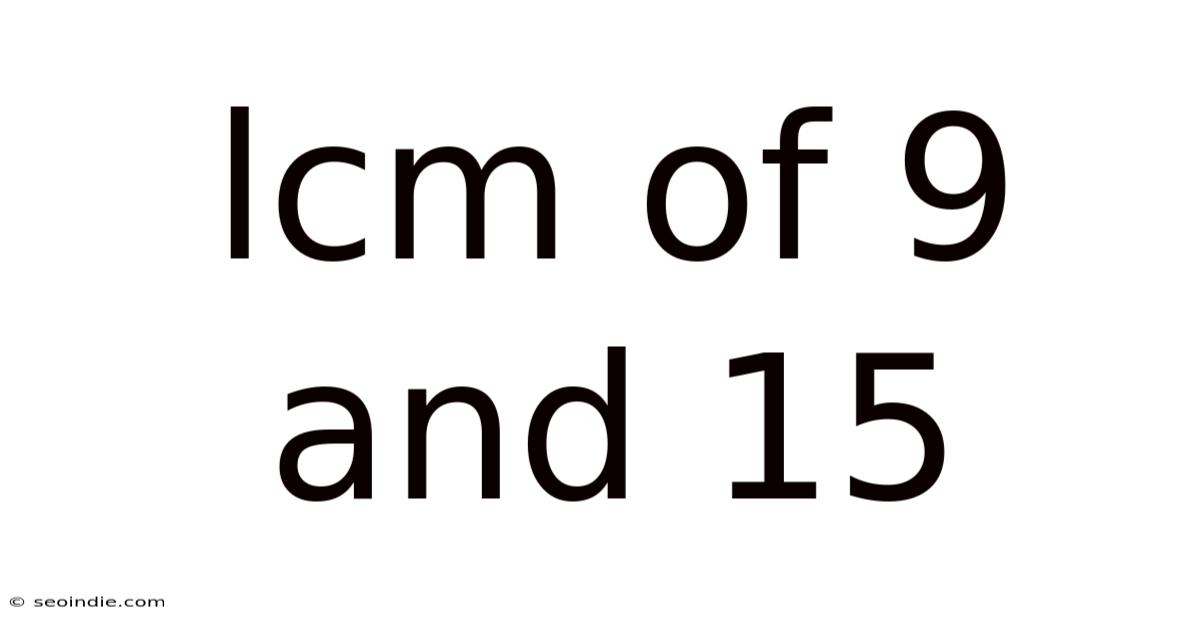
Table of Contents
Finding the Least Common Multiple (LCM) of 9 and 15: A Comprehensive Guide
Finding the Least Common Multiple (LCM) is a fundamental concept in mathematics, crucial for solving various problems in arithmetic, algebra, and even more advanced fields. This article provides a comprehensive guide to understanding and calculating the LCM of 9 and 15, exploring different methods and illustrating the underlying mathematical principles. We'll delve beyond simply finding the answer to explore the why behind the methods, ensuring a solid understanding of this important concept.
Introduction: What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. Think of it as the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is crucial for various applications, including simplifying fractions, solving problems involving time intervals, and working with ratios and proportions. In this article, we will focus on calculating the LCM of 9 and 15, providing multiple approaches to solidify your understanding.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We start by listing the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 45. Therefore, the LCM of 9 and 15 is 45. This method is simple and intuitive but can become cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factorization is expressing a number as a product of its prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 15: 3 x 5
To find the LCM using prime factorization:
- Identify the prime factors: We have 3 and 5.
- Find the highest power of each prime factor: The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5¹ (from the factorization of 15).
- Multiply the highest powers: 3² x 5 = 9 x 5 = 45
Therefore, the LCM of 9 and 15 is 45 using the prime factorization method. This method is generally preferred for larger numbers because it's more systematic and less prone to errors than simply listing multiples.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Let's first find the GCD of 9 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (9): 15 ÷ 9 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (6): 9 ÷ 6 = 1 with a remainder of 3.
- Repeat: 6 ÷ 3 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD. In this case, the GCD(9, 15) = 3.
Now, we can use the formula:
LCM(9, 15) x GCD(9, 15) = 9 x 15 LCM(9, 15) x 3 = 135 LCM(9, 15) = 135 ÷ 3 = 45
This method is also efficient, especially when dealing with larger numbers, as finding the GCD is often simpler than directly finding the LCM, particularly when using the Euclidean algorithm.
Understanding the Mathematics Behind LCM
The LCM represents the smallest point where the multiples of two numbers coincide. Visually, imagine two number lines representing multiples of 9 and 15. The LCM is the smallest value where both number lines intersect. Prime factorization helps us understand this intersection by breaking down the numbers into their fundamental building blocks. By finding the highest power of each prime factor present in both numbers, we ensure we capture the smallest multiple that encompasses all factors.
The relationship between LCM and GCD stems from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This unique representation allows us to efficiently determine both LCM and GCD, and the relationship between them provides an alternative, and sometimes more efficient, route to calculating the LCM.
Applications of LCM
The concept of LCM finds application in various real-world scenarios:
- Scheduling: Determining when events will occur simultaneously. For example, if two buses depart from the same stop at different intervals, the LCM helps find when they will depart together again.
- Fractions: Finding the least common denominator when adding or subtracting fractions.
- Measurement: Converting between different units of measurement.
- Patterning: Identifying recurring patterns in sequences.
Frequently Asked Questions (FAQ)
-
Q: What if I want to find the LCM of more than two numbers?
- A: You can extend the prime factorization method or the GCD method to include more numbers. For prime factorization, consider all the prime factors of all the numbers and take the highest power of each. For the GCD method, you would need to repeatedly apply the method to find the GCD of the entire set, and then use the extension of the formula: LCM(a, b, c) * GCD(a, b, c) = a * b * c.
-
Q: Is there a formula for the LCM of two numbers that doesn't involve the GCD?
- A: While the formula involving the GCD is often efficient, the LCM can be directly calculated using prime factorization without explicitly calculating the GCD.
-
Q: Why is the prime factorization method considered more efficient for larger numbers?
- A: Listing multiples becomes increasingly tedious and error-prone for larger numbers. Prime factorization provides a systematic approach that’s less reliant on manual counting and more resistant to errors.
Conclusion
Finding the LCM of 9 and 15, while seemingly a simple task, offers a gateway to understanding deeper mathematical concepts. We've explored three distinct methods – listing multiples, prime factorization, and the GCD method – each offering a unique perspective on this fundamental mathematical operation. Understanding these methods not only allows you to efficiently calculate the LCM but also provides valuable insight into number theory and its wide-ranging applications. Mastering the LCM is a crucial stepping stone in your mathematical journey, opening doors to more complex and challenging problems in the future. Remember to choose the method best suited to the numbers you are working with – for small numbers, listing multiples might suffice, but for larger numbers, prime factorization or the GCD method proves more efficient and less error-prone. By understanding the underlying principles, you can confidently tackle any LCM problem you encounter.
Latest Posts
Latest Posts
-
Active And Passive Voice Worksheet
Sep 20, 2025
-
Words That End With Ne
Sep 20, 2025
-
Distinguish Between Antibody And Antigen
Sep 20, 2025
-
English Words Ending With Boa
Sep 20, 2025
-
300 Meters In Square Feet
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.