Lcm Of 8 7 6
seoindie
Sep 13, 2025 · 6 min read
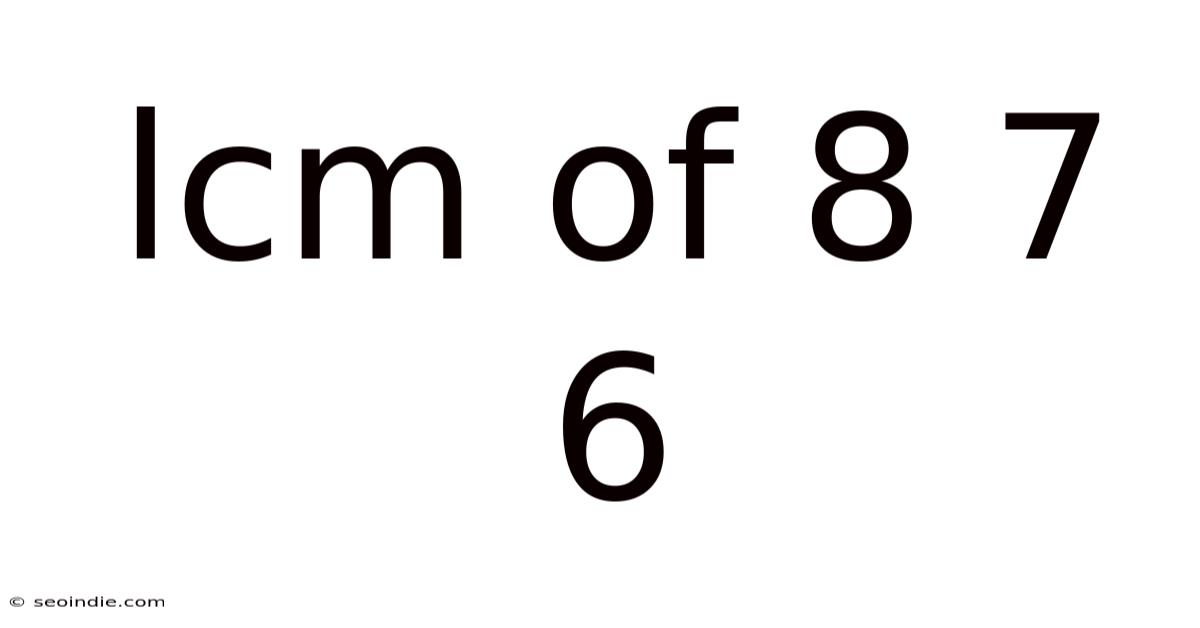
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 7, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications, from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will explore how to determine the LCM of 8, 7, and 6, detailing different methods and providing a deeper understanding of the underlying principles. We'll move beyond simply finding the answer and delve into why these methods work, making this a valuable resource for students and anyone looking to refresh their mathematical skills.
Introduction: Understanding LCM
The Least Common Multiple (LCM) is the smallest positive integer that is a multiple of all the numbers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. Understanding LCM is crucial for operations involving fractions, especially when adding or subtracting fractions with different denominators. Finding a common denominator is essentially finding the LCM of the denominators.
Our goal is to find the LCM of 8, 7, and 6. This seemingly simple problem provides an excellent opportunity to explore several methods for calculating the LCM, each with its own advantages and applications.
Method 1: Listing Multiples
The most straightforward method, particularly useful for smaller numbers, is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168…
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168…
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126, 132, 138, 144, 150, 156, 162, 168…
By comparing the lists, we can see that the smallest number that appears in all three lists is 168. Therefore, the LCM(8, 7, 6) = 168. This method is simple to understand but can become cumbersome with larger numbers or a greater number of numbers in the set.
Method 2: Prime Factorization
A more efficient and powerful method, especially for larger numbers, involves prime factorization. This method relies on expressing each number as a product of its prime factors.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 7 = 7 (7 is a prime number)
- 6 = 2 x 3
-
Identify the highest power of each prime factor:
- The prime factors present are 2, 3, and 7.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
-
Multiply the highest powers together:
- LCM(8, 7, 6) = 2³ x 3 x 7 = 8 x 3 x 7 = 168
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. The prime factorization method provides a systematic approach that avoids the tedious process of comparing long lists of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the Greatest Common Divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes more complex. Let's illustrate this with our example:
-
Find the GCD of 8 and 7: The GCD of 8 and 7 is 1, as they share no common factors other than 1.
-
Find the GCD of (the GCD of 8 and 7) and 6: The GCD of 1 and 6 is 1.
The formula, while directly applicable to two numbers, isn't as straightforward to extend for three or more numbers. While you could find the LCM of 8 and 7 first, and then find the LCM of that result and 6, this becomes less efficient than prime factorization for larger numbers. This method highlights the interconnectedness of LCM and GCD but isn't the most practical for this particular problem.
A Deeper Dive into Prime Factorization: Why it Works
The prime factorization method's efficiency stems from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This unique representation allows us to systematically find the LCM. By taking the highest power of each prime factor present in the numbers, we ensure that we capture all the factors necessary to create a multiple of each of the original numbers. Any smaller number would necessarily be missing at least one prime factor required for divisibility by one of the original numbers.
Applications of LCM
The LCM finds applications in various areas of mathematics and beyond:
-
Adding and Subtracting Fractions: Finding a common denominator is crucial for adding and subtracting fractions. The common denominator is the LCM of the denominators.
-
Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at the same stop, machines completing cycles at the same time).
-
Cyclic Patterns: Analyzing repeating patterns or cycles (e.g., planetary orbits, repeating musical patterns).
-
Number Theory: LCM plays a significant role in various number theory problems, including modular arithmetic and Diophantine equations.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors? A: If the numbers are relatively prime (i.e., their GCD is 1), their LCM is simply their product. For example, LCM(5, 7) = 5 x 7 = 35.
-
Q: Can I use a calculator to find the LCM? A: Many scientific calculators have a built-in function to calculate the LCM. However, understanding the underlying methods is crucial for problem-solving beyond simple calculations.
-
Q: Is there a limit to the number of numbers for which I can find the LCM? A: No, the methods described, particularly prime factorization, can be applied to find the LCM of any number of integers.
Conclusion
Finding the LCM of 8, 7, and 6, as demonstrated, involves various methods, each offering different levels of efficiency. While listing multiples is intuitive for smaller numbers, prime factorization provides a more efficient and systematic approach for larger numbers. Understanding the underlying principles, like the fundamental theorem of arithmetic and the relationship between LCM and GCD, provides a deeper appreciation of this fundamental mathematical concept. The LCM is a powerful tool with wide-ranging applications, making its mastery essential for anyone pursuing further study in mathematics or related fields. The ability to confidently determine the LCM of any set of numbers empowers you to solve complex problems and strengthens your foundational mathematical skills. Remember that consistent practice and understanding the "why" behind the methods are key to mastering this crucial concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 8 7 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.