Lcm Of 6 And 5
seoindie
Sep 17, 2025 · 6 min read
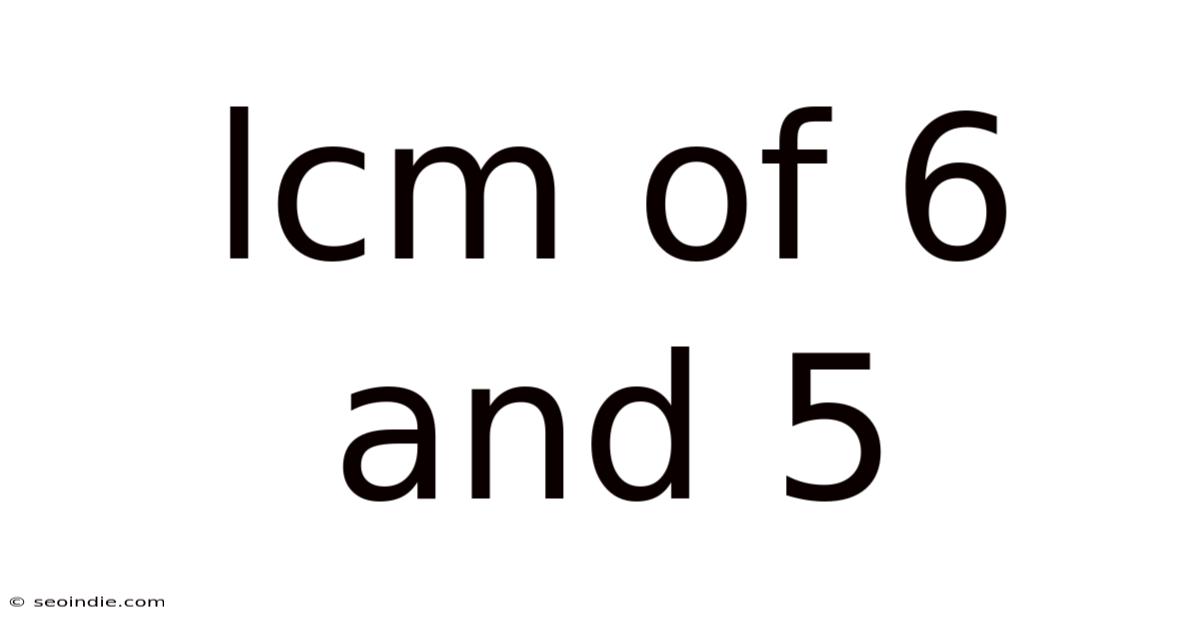
Table of Contents
Finding the Least Common Multiple (LCM) of 6 and 5: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a solid foundation for more advanced mathematical concepts. This article will explore the LCM of 6 and 5 in detail, explaining several approaches, their applications, and delving into the theoretical underpinnings. We’ll move beyond simply stating the answer and delve into why the answer is what it is, ensuring a thorough and insightful understanding.
Introduction: What is the Least Common Multiple?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number that is divisible by both 2 and 3. Understanding LCMs is crucial in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like modular arithmetic.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to find the LCM of 6 and 5.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
By examining both lists, we observe that the smallest number common to both is 30. Therefore, the LCM of 6 and 5 is 30. This method works well for smaller numbers but can become cumbersome with larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
-
Find the prime factorization of each number:
- 6 = 2 × 3
- 5 = 5 (5 is a prime number)
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
- LCM(6, 5) = 2 × 3 × 5 = 30
This method is more systematic and efficient, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula connecting the LCM and GCD:
LCM(a, b) × GCD(a, b) = a × b
-
Find the GCD of 6 and 5:
The GCD of 6 and 5 is 1, as 1 is the only common divisor.
-
Apply the formula:
LCM(6, 5) × GCD(6, 5) = 6 × 5 LCM(6, 5) × 1 = 30 LCM(6, 5) = 30
This method is particularly useful when you already know the GCD of the numbers. Finding the GCD can be done using the Euclidean algorithm, a very efficient method for larger numbers.
Understanding the LCM: A Deeper Look
The LCM represents the cycle length before the multiples of both numbers repeat. Imagine two gears rotating. The LCM represents the number of rotations after which both gears will simultaneously be in their starting position. This concept has applications in various fields, such as scheduling and cyclical events.
For instance, if one task repeats every 6 days and another every 5 days, the LCM (30) indicates that both tasks will coincide every 30 days. This is a powerful concept with real-world applications in project management, logistics, and even understanding natural cycles.
Applications of LCM
The concept of LCM has wide-ranging applications across various fields:
- Fraction Addition and Subtraction: To add or subtract fractions with different denominators, finding the LCM of the denominators is necessary to find a common denominator.
- Ratio and Proportion Problems: LCM is used to solve problems involving ratios and proportions where we need to find equivalent ratios with common terms.
- Scheduling and Cyclical Events: As mentioned earlier, LCM helps determine when events with different cycles will occur simultaneously. This is used in scheduling tasks, planning events, and even in understanding astronomical phenomena.
- Music Theory: The LCM is used in music theory to determine the least common denominator for musical intervals.
- Computer Science: In computer programming, LCM is used in algorithms dealing with cyclical patterns and timing.
Frequently Asked Questions (FAQ)
Q1: What if I want to find the LCM of more than two numbers?
A: The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you'll include all prime factors from all numbers and take the highest power of each. For the GCD method, you can find the GCD of the numbers iteratively.
Q2: Is there a formula for the LCM of three or more numbers?
A: There isn't a single compact formula like the one for two numbers, but the principles of prime factorization remain the same. You find the prime factorization of each number, take the highest power of each prime factor, and multiply them together.
Q3: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other. For example, LCM(4, 8) = 8.
Q4: What is the difference between LCM and GCD?
A: The LCM is the smallest common multiple, while the GCD is the largest common divisor. They are inversely related; a larger GCD means a smaller LCM, and vice-versa.
Q5: How can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM. Consult your calculator's manual for instructions. Online calculators are also readily available.
Conclusion
Finding the LCM of 6 and 5, which is 30, might seem like a trivial task at first glance. However, understanding the different methods—listing multiples, prime factorization, and using the GCD—provides a deeper understanding of fundamental mathematical concepts. This understanding extends far beyond basic arithmetic, providing a foundation for solving more complex problems in various fields, emphasizing the practical relevance of this seemingly simple concept. The ability to calculate the LCM efficiently is a valuable skill, not just in mathematics, but also in various practical applications. Mastering this concept solidifies your understanding of number theory and its real-world relevance.
Latest Posts
Latest Posts
-
Equilateral Triangle Center Of Mass
Sep 17, 2025
-
What Does U N O Stand For
Sep 17, 2025
-
Dialog Writing Between Two Friends
Sep 17, 2025
-
220 Meters Squared To Feet
Sep 17, 2025
-
Presents That Start With E
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.