Lcm Of 6 8 9
seoindie
Sep 17, 2025 · 6 min read
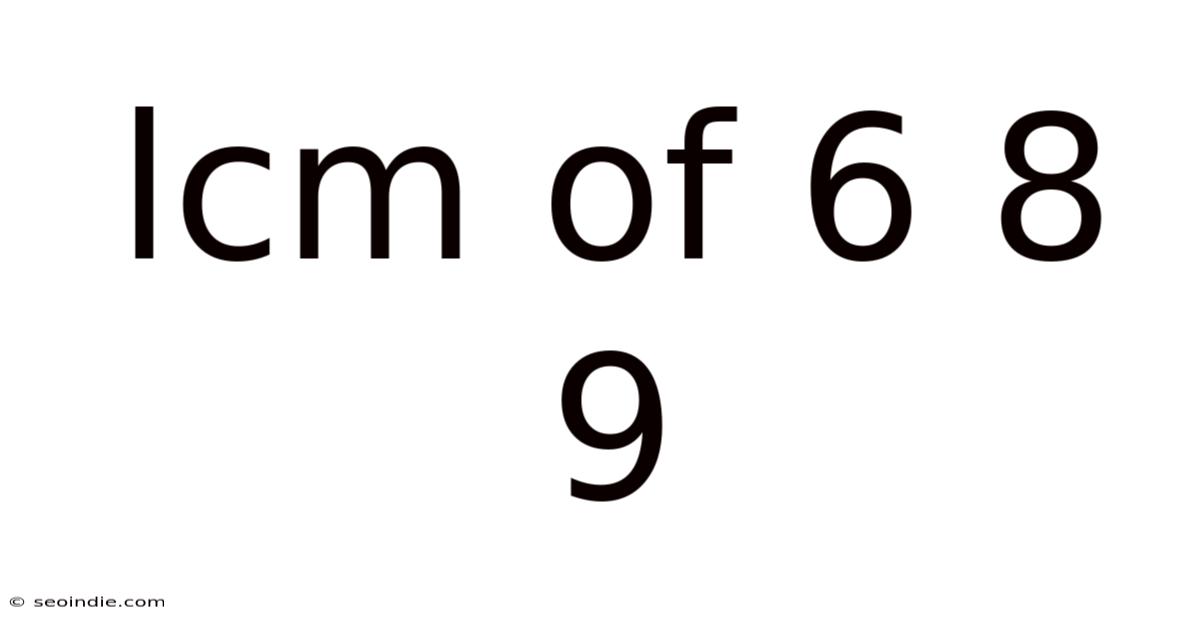
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 8, and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving real-world problems involving cyclical events. This article will delve into a comprehensive understanding of how to calculate the LCM of 6, 8, and 9, exploring different methods and providing a deeper insight into the underlying mathematical principles. We'll cover everything from basic definitions to advanced techniques, ensuring a clear and thorough grasp of the subject.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 6, 8, and 9, let's establish a solid understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider finding the LCM of 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 72, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
Looking at the lists, we can see that the smallest number that appears in all three lists is 72. Therefore, the LCM of 6, 8, and 9 is 72. This method is effective for smaller numbers but becomes cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
This is a more efficient and systematic method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's find the prime factorization of each number:
- 6 = 2 × 3
- 8 = 2 × 2 × 2 = 2³
- 9 = 3 × 3 = 3²
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
To find the LCM, we multiply these highest powers together:
LCM(6, 8, 9) = 2³ × 3² = 8 × 9 = 72
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a powerful relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This can be extended to more than two numbers, although the calculation becomes slightly more involved. While not as direct for multiple numbers as prime factorization, it demonstrates a fundamental mathematical connection.
Let's first find the GCD of 6, 8, and 9 using the Euclidean algorithm or prime factorization. The GCD(6, 8, 9) = 1 (because there are no common factors other than 1).
While the direct relationship formula doesn't easily extend to three numbers, the underlying principle of finding common factors is still relevant. We've already established the LCM using prime factorization as 72.
Applications of LCM
Understanding and calculating the LCM has numerous applications in various fields:
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions with different denominators. This allows us to find a common denominator, simplifying the calculation.
-
Scheduling: LCM is used in scheduling problems, such as determining when events that occur at different intervals will coincide. For example, if two buses leave a station at different intervals, the LCM helps determine when they will depart at the same time again.
-
Modular Arithmetic: The concept of LCM is fundamental in modular arithmetic, used extensively in cryptography and computer science.
-
Cyclic Patterns: LCM helps analyze and predict cyclical patterns in various phenomena, like the repeating cycles of planetary motion or the periodic behavior of certain physical systems.
-
Real-world Problems: LCM helps solve various real-world problems involving repetitive events or cycles, such as aligning machinery in manufacturing processes or planning work schedules.
Step-by-Step Guide to Finding the LCM of Any Set of Numbers
To solidify our understanding, let's outline a general step-by-step procedure for finding the LCM of any set of numbers:
-
Prime Factorization: Find the prime factorization of each number in the set. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
-
Identify Highest Powers: For each distinct prime factor that appears in the factorizations, identify the highest power of that prime factor.
-
Multiply Highest Powers: Multiply together all the highest powers of the distinct prime factors identified in step 2. The result is the LCM of the original set of numbers.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The Least Common Multiple (LCM) is the smallest number that is a multiple of all the given numbers. The Greatest Common Divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides all the given numbers without leaving a remainder.
Q: Can the LCM of two numbers be smaller than both numbers?
A: No, the LCM of two numbers can never be smaller than either of the numbers. It's always greater than or equal to the largest of the two numbers.
Q: What if the numbers have no common factors other than 1?
A: If the numbers have no common factors other than 1, their GCD is 1. In such cases, their LCM is simply the product of the numbers. For instance, the LCM of 7 and 11 (which are both prime and therefore have no common factors other than 1) is 77 (7 x 11).
Q: Are there any other methods for finding the LCM besides the ones discussed?
A: While prime factorization and listing multiples are the most common methods, there are other algorithms and techniques, especially for larger sets of numbers or within the context of specialized computational environments. These often rely on more advanced mathematical principles and computational optimizations.
Q: How does the LCM relate to the concept of fractions?
A: When adding or subtracting fractions, finding the LCM of the denominators is crucial. This ensures that we can work with equivalent fractions that have a common denominator, simplifying the process.
Conclusion
Finding the least common multiple is a fundamental skill with broad applications in mathematics and beyond. This article explored various methods for calculating the LCM, emphasizing the efficiency and elegance of the prime factorization method. We've seen how the LCM helps solve problems related to fractions, scheduling, and cyclical patterns. Understanding the LCM lays a strong foundation for further exploration into more advanced mathematical concepts. By mastering these techniques, you'll be equipped to solve a wide range of mathematical problems efficiently and confidently. Remember, practice is key to solidifying your understanding and building your problem-solving skills!
Latest Posts
Latest Posts
-
Greatest Common Factor Of 19
Sep 17, 2025
-
Soda Ash Vs Sodium Carbonate
Sep 17, 2025
-
According To Kirchhoffs Voltage Law
Sep 17, 2025
-
Infinite Line Charge Electric Field
Sep 17, 2025
-
Is 0 001 Less Than 0 05
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 8 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.