Lcm Of 50 And 35
seoindie
Sep 17, 2025 · 6 min read
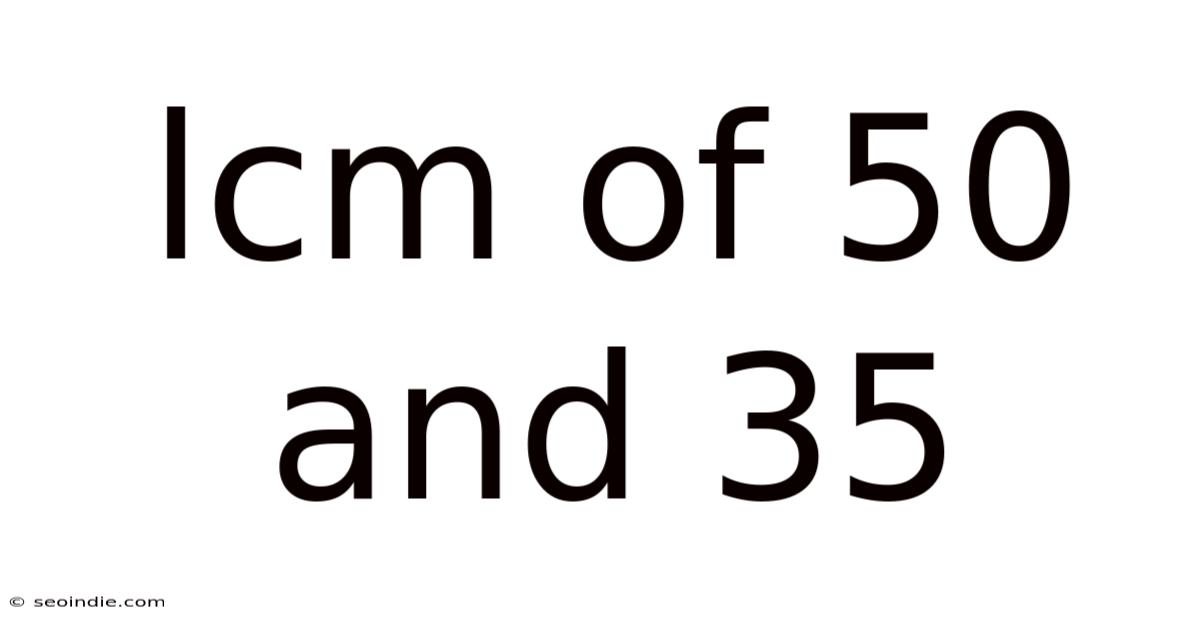
Table of Contents
Finding the LCM of 50 and 35: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications ranging from simple fraction arithmetic to complex scheduling problems. This article provides a thorough explanation of how to calculate the LCM of 50 and 35, exploring various methods and delving into the underlying mathematical principles. We'll move beyond simply finding the answer to understand why the methods work, building a solid foundation in number theory.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's define what the least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Understanding this definition is crucial to grasping the different methods we'll explore.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 50 and 35. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 50: 50, 100, 150, 200, 250, 300, 350, ...
- Multiples of 35: 35, 70, 105, 140, 175, 210, 245, 280, 315, 350, ...
By comparing the lists, we can see that the smallest multiple common to both 50 and 35 is 350. Therefore, the LCM(50, 35) = 350. This method is simple to visualize but can become tedious with larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It relies on expressing each number as a product of its prime factors. A prime factor is a number divisible only by 1 and itself (e.g., 2, 3, 5, 7, 11...).
Step 1: Find the prime factorization of each number.
- 50: 2 x 5 x 5 = 2 x 5²
- 35: 5 x 7
Step 2: Identify the highest power of each prime factor present in either factorization.
In our case, the prime factors are 2, 5, and 7. The highest power of 2 is 2¹ (from 50), the highest power of 5 is 5² (from 50), and the highest power of 7 is 7¹ (from 35).
Step 3: Multiply the highest powers together.
LCM(50, 35) = 2¹ x 5² x 7¹ = 2 x 25 x 7 = 350
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or multiple numbers simultaneously. The prime factorization method provides a systematic approach that avoids the potential for oversight.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a useful formula connecting them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where |a x b| represents the absolute value of the product of 'a' and 'b'. This means we can find the LCM if we know the GCD.
Step 1: Find the GCD of 50 and 35 using the Euclidean algorithm.
The Euclidean algorithm is an efficient method for finding the GCD.
- Divide the larger number (50) by the smaller number (35): 50 = 1 x 35 + 15
- Replace the larger number with the remainder (15) and repeat: 35 = 2 x 15 + 5
- Repeat until the remainder is 0: 15 = 3 x 5 + 0
The last non-zero remainder is the GCD, which is 5.
Step 2: Apply the formula:
LCM(50, 35) = (50 x 35) / 5 = 1750 / 5 = 350
This method leverages the relationship between LCM and GCD, providing an alternative approach to calculating the LCM. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers efficiently.
A Deeper Dive into Prime Factorization
The prime factorization method highlights a fundamental concept in number theory: the fundamental theorem of arithmetic. This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This unique factorization is the cornerstone of many number-theoretic calculations, including finding the LCM and GCD. Understanding this theorem allows us to appreciate the elegance and power of the prime factorization method. The uniqueness of the prime factorization ensures that we'll always arrive at the same LCM regardless of the order in which we list the prime factors.
Applications of LCM
The concept of LCM has numerous practical applications:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop, machines completing cycles) often involves calculating the LCM of the time intervals.
- Modular Arithmetic: LCM plays a critical role in solving problems in modular arithmetic, which is used in cryptography and other fields.
- Music Theory: The LCM is used to find the least common period of repeating musical patterns.
Frequently Asked Questions (FAQ)
-
Q: What if I use different prime factorizations for the same number? Will I get a different LCM?
A: No. The fundamental theorem of arithmetic guarantees that the prime factorization of any number is unique (except for the order of the factors). Therefore, you will always obtain the same LCM, regardless of how you factorize the numbers.
-
Q: Can I use the LCM method for more than two numbers?
A: Yes, all three methods can be extended to handle more than two numbers. For prime factorization, you would consider all the prime factors from all the numbers and take the highest power of each. For the GCD-based method, you would iteratively compute the GCD of pairs of numbers and then use the formula repeatedly. The listing multiples method becomes increasingly inefficient with more numbers.
-
Q: Why is the LCM always greater than or equal to the larger of the two numbers?
A: The LCM must be a multiple of both numbers. Since it's the least common multiple, it will be at least as large as the larger of the two numbers.
-
Q: What if the two numbers are relatively prime (i.e., their GCD is 1)?
A: If the GCD is 1, then the LCM is simply the product of the two numbers. This is a special case of the GCD-based method.
Conclusion
Finding the LCM of 50 and 35, while seemingly a simple task, provides a gateway to understanding fundamental concepts in number theory. We've explored three distinct methods – listing multiples, prime factorization, and the GCD approach – each offering unique insights and efficiencies. Mastering these methods equips you not only to calculate LCMs but also to appreciate the deeper mathematical principles underpinning this essential concept. Remember, the chosen method often depends on the size of the numbers involved and your comfort level with different mathematical techniques. Understanding the underlying principles, however, will empower you to tackle any LCM problem confidently.
Latest Posts
Latest Posts
-
Total Biodiversity Hotspots In World
Sep 17, 2025
-
Winter Things Starting With W
Sep 17, 2025
-
Lcm Of 3 9 12
Sep 17, 2025
-
What Times What Equals 60
Sep 17, 2025
-
Tartaric Acid Vs Citric Acid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 50 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.