Lcm Of 5 6 7
seoindie
Sep 25, 2025 · 6 min read
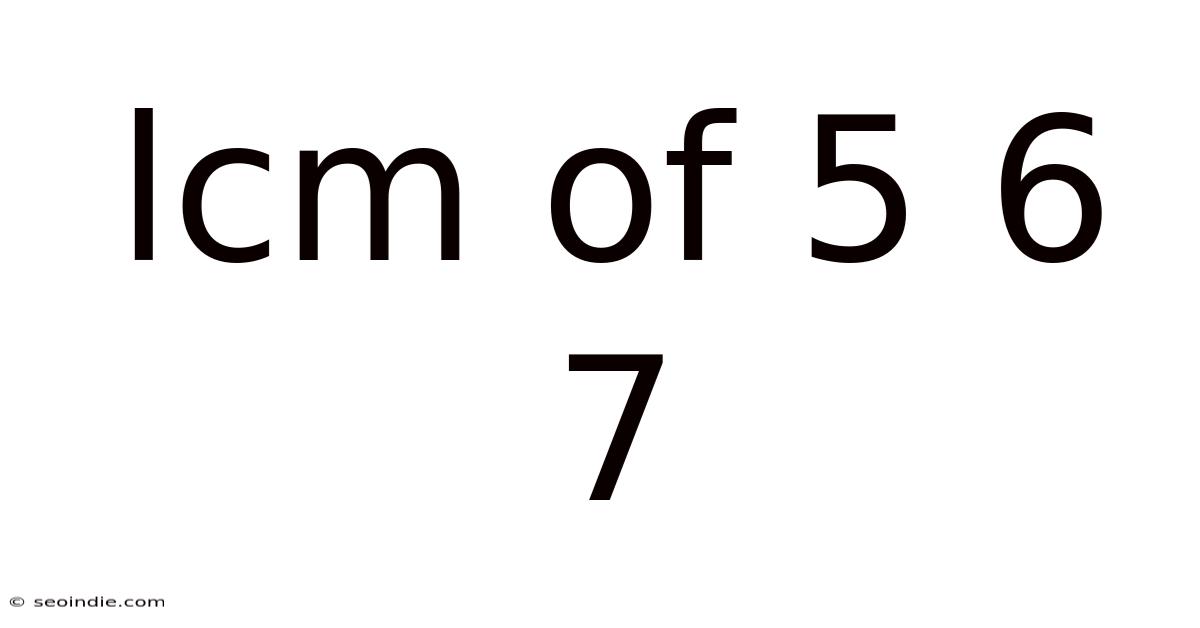
Table of Contents
Finding the Least Common Multiple (LCM) of 5, 6, and 7: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article provides a comprehensive guide on how to calculate the LCM of 5, 6, and 7, explaining the underlying principles and offering different methods to solve this seemingly simple, yet important, mathematical problem. We'll explore various techniques, from listing multiples to using prime factorization, ensuring a deep understanding for learners of all levels.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's clarify what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3. Understanding this fundamental definition is key to mastering LCM calculations.
Method 1: Listing Multiples
This method is straightforward, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126, 210...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 210...
By comparing the lists, we observe that the smallest number common to all three lists is 210. Therefore, the LCM of 5, 6, and 7 is 210. This method is simple to visualize but can become cumbersome with larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's find the prime factorization of 5, 6, and 7:
- 5: 5 (5 is a prime number)
- 6: 2 x 3
- 7: 7 (7 is a prime number)
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, 5, and 7.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
- The highest power of 7 is 7¹ = 7.
Multiplying these highest powers together: 2 x 3 x 5 x 7 = 210. Therefore, the LCM of 5, 6, and 7 is 210. This method is generally more efficient and less prone to error than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This formula can be extended to more than two numbers, but it becomes more complex. While we could use this for two numbers at a time (finding the LCM of 5 and 6, then finding the LCM of that result and 7), it's generally less efficient than prime factorization for this particular problem.
For a quick recap:
- GCD: The greatest common divisor is the largest positive integer that divides each of the integers without leaving a remainder. The GCD of 5, 6, and 7 is 1 because they share no common divisors other than 1.
Let's illustrate how to use this method with a simpler example: Finding the LCM of 12 and 18.
-
Find the GCD: The prime factorization of 12 is 2² x 3, and the prime factorization of 18 is 2 x 3². The GCD is 2 x 3 = 6.
-
Apply the formula: LCM(12, 18) * GCD(12, 18) = 12 * 18 LCM(12, 18) * 6 = 216 LCM(12, 18) = 216 / 6 = 36
This demonstrates the relationship between LCM and GCD, but the prime factorization method remains more direct and efficient for our initial problem.
Why is finding the LCM important?
The ability to calculate LCMs is essential in many areas of mathematics and beyond:
-
Fraction addition and subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
-
Scheduling problems: Determining when events will occur simultaneously. For example, if three buses depart at different intervals, finding the LCM helps determine when they will all depart at the same time.
-
Modular arithmetic: Used in cryptography and computer science, LCM plays a vital role in solving congruences.
-
Music theory: Determining the least common multiple of note durations helps musicians understand rhythmic relationships.
-
Engineering and design: In areas such as gear ratios and frequency synchronization, LCM is crucial for optimizing designs.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always larger than the largest number in the set?
A1: Yes, the LCM will always be greater than or equal to the largest number in the set. In our case, 210 is greater than 7. This is because the LCM must be divisible by all numbers in the set.
Q2: What if the numbers have common factors? Does that affect the LCM calculation?
A2: Yes, it does. The prime factorization method automatically accounts for common factors. If numbers share common factors, the LCM will be smaller than the simple product of all the numbers.
Q3: Can I use a calculator to find the LCM?
A3: Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of multiple numbers. However, understanding the underlying principles and methods is crucial for grasping the concept and solving problems effectively.
Q4: Are there other methods to find the LCM besides the ones mentioned?
A4: While the methods described are the most common and efficient, more advanced algorithms exist for calculating the LCM of very large numbers. These algorithms are often employed in computer science for optimization purposes.
Conclusion
Finding the least common multiple of 5, 6, and 7, although seemingly simple, provides a stepping stone to understanding a crucial mathematical concept with broad applications. We've explored three methods: listing multiples, prime factorization (the most efficient), and a method involving the GCD. The prime factorization method is particularly useful for its efficiency and clarity, especially when working with larger numbers. Mastering LCM calculations is vital for success in various mathematical fields and their related applications. Understanding the concept and its different approaches empowers you to tackle more complex mathematical problems with confidence. Remember to practice regularly to solidify your understanding and build your problem-solving skills. The journey of learning mathematics is continuous, and every step forward strengthens your abilities.
Latest Posts
Latest Posts
-
2 Times What Equals 36
Sep 25, 2025
-
Constitutional Isomers Vs Conformational Isomers
Sep 25, 2025
-
What Is 1 4 In Percentage
Sep 25, 2025
-
Gcf Of 15 And 8
Sep 25, 2025
-
Periodic Table Metal Nonmetal Metalloid
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 6 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.