Lcm Of 39 And 26
seoindie
Sep 15, 2025 · 6 min read
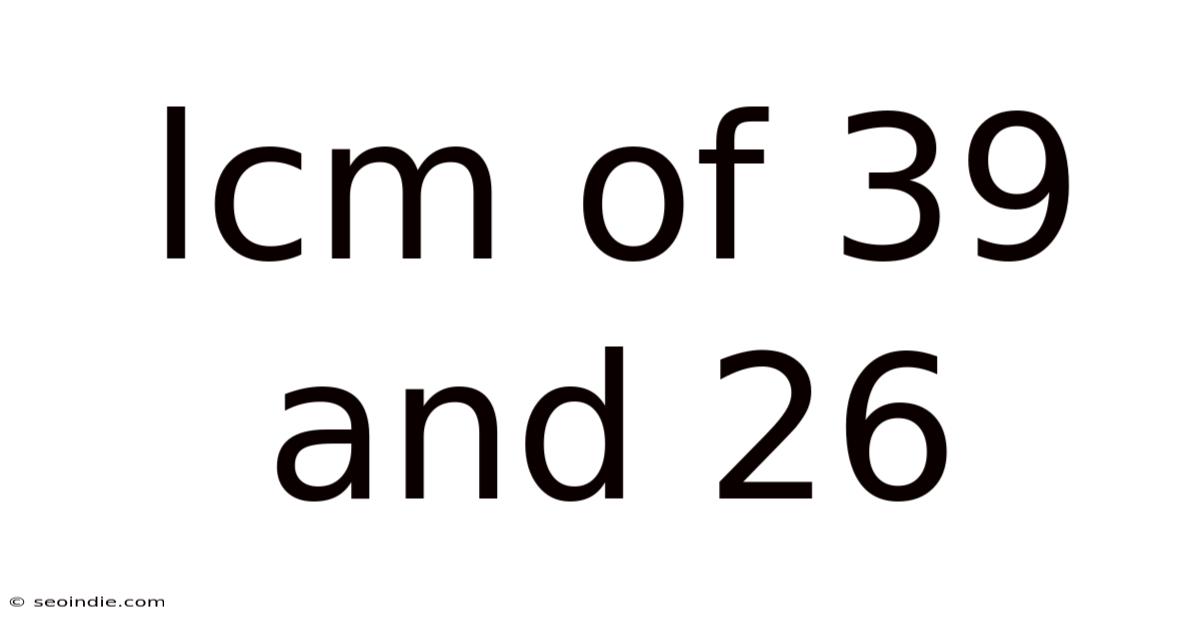
Table of Contents
Finding the LCM of 39 and 26: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in arithmetic with wide-ranging applications in various fields, from scheduling to music theory. This article provides a comprehensive guide to calculating the LCM of 39 and 26, exploring different methods and delving deeper into the underlying mathematical principles. We'll move beyond simply finding the answer and explore the why behind the calculations, ensuring a thorough understanding of this important mathematical concept.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 39 and 26, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. Think of it as the smallest common "meeting point" for multiples of the given numbers.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 39: 39, 78, 117, 156, 195, 234, 273, 312, 351, 390…
- Multiples of 26: 26, 52, 78, 104, 130, 156, 182, 208, 234, 260…
By comparing the two lists, we can see that the smallest number that appears in both lists is 78. Therefore, the LCM of 39 and 26 is 78.
This method works well for smaller numbers but becomes increasingly cumbersome and time-consuming as the numbers get larger.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is using prime factorization. This method involves breaking down each number into its prime factors – the prime numbers that multiply together to give the original number.
- Prime factorization of 39: 39 = 3 x 13
- Prime factorization of 26: 26 = 2 x 13
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together.
In this case, the prime factors are 2, 3, and 13. The highest power of 2 is 2¹, the highest power of 3 is 3¹, and the highest power of 13 is 13¹. Therefore, the LCM is 2 x 3 x 13 = 78.
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related by a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, we need to find the GCD of 39 and 26. We can use the Euclidean algorithm for this:
- Divide the larger number (39) by the smaller number (26): 39 ÷ 26 = 1 with a remainder of 13.
- Replace the larger number with the smaller number (26) and the smaller number with the remainder (13): 26 ÷ 13 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 13.
Now we can use the formula:
LCM(39, 26) = (|39 x 26|) / GCD(39, 26) = (1014) / 13 = 78
Why is LCM Important?
Understanding LCM isn't just about solving mathematical problems; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine you have two machines that need regular maintenance. One requires servicing every 39 days, and the other every 26 days. To find out when both machines will need servicing simultaneously, you need to calculate the LCM. In this case, the LCM of 39 and 26 is 78 days. Both machines will need servicing together every 78 days.
-
Fractions: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to find a common denominator. This allows you to add or subtract the fractions easily.
-
Music: Musical rhythms often involve finding common multiples of different note values. The LCM helps determine when different rhythmic patterns will align.
-
Project Management: In project planning, if different tasks have varying durations, LCM can help determine the optimal time for project milestones or completion points.
A Deeper Dive into Prime Factorization
The prime factorization method is a powerful tool because it reveals the fundamental building blocks of a number. Every integer greater than 1 can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This unique factorization allows us to systematically determine the LCM and GCD of numbers. Understanding prime factorization provides a deeper insight into the structure of numbers and their relationships.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are inversely related, as demonstrated by the formula relating them.
-
Can I use a calculator to find the LCM? Yes, many scientific calculators have built-in functions to calculate the LCM and GCD of numbers.
-
What if I have more than two numbers? The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you'd consider all prime factors across all numbers, taking the highest power of each. For the GCD method, you can find the GCD of two numbers, then find the GCD of the result and the next number, and so on.
-
Why is 78 the smallest common multiple of 39 and 26? Because 78 is the smallest positive integer that is divisible by both 39 and 26 without leaving a remainder. Any other common multiple will be a larger multiple of 78.
Conclusion
Calculating the LCM of 39 and 26, whether through listing multiples, prime factorization, or using the GCD, results in the same answer: 78. While the listing method is suitable for smaller numbers, prime factorization and the GCD method offer more efficient approaches, especially for larger numbers. Understanding the concept of LCM extends beyond simple calculation; it holds practical significance in various fields and provides deeper insight into the structure of numbers. Mastering LCM calculations enhances your mathematical skills and provides a valuable tool for problem-solving in numerous contexts. Remember to choose the method most appropriate for the numbers involved and always strive to understand the underlying mathematical principles to build a stronger foundation in arithmetic.
Latest Posts
Latest Posts
-
How Does An Amoeba Reproduce
Sep 15, 2025
-
Difference Between Alloy And Composite
Sep 15, 2025
-
Where To Purchase Sodium Silicate
Sep 15, 2025
-
Electron Dot Symbol For Aluminum
Sep 15, 2025
-
Adverbs That Start With M
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 39 And 26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.