Lcm Of 30 And 48
seoindie
Sep 25, 2025 · 7 min read
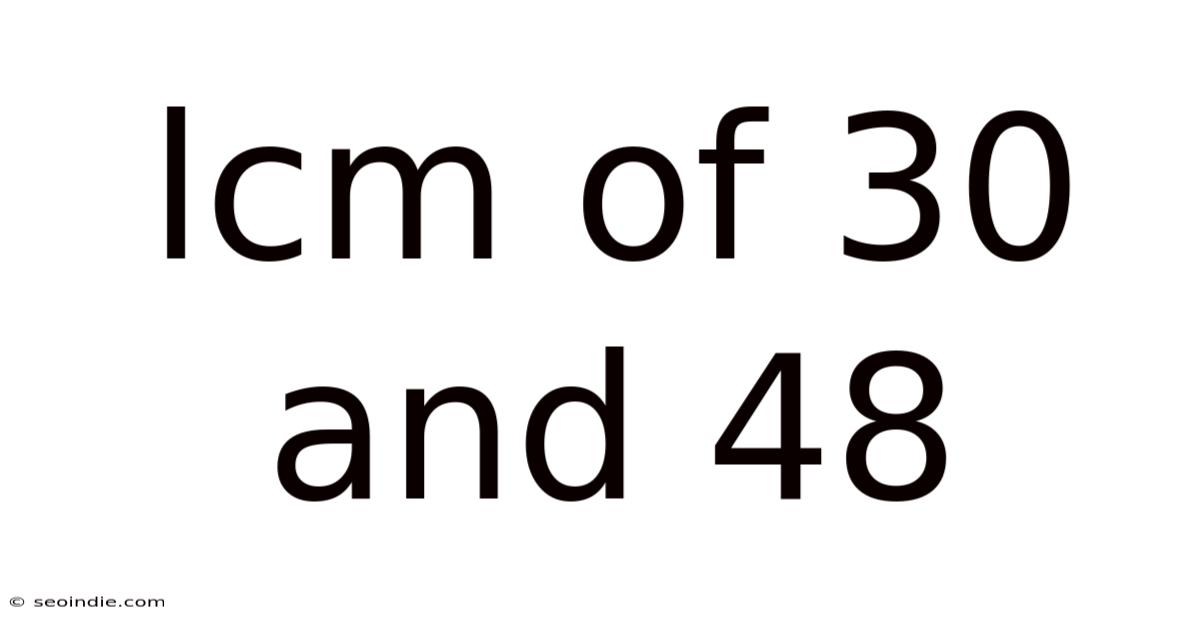
Table of Contents
Finding the Least Common Multiple (LCM) of 30 and 48: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, with applications ranging from simple fraction addition to complex scheduling problems. This comprehensive guide will explore how to find the LCM of 30 and 48 using several different methods, explaining the underlying mathematical principles and providing examples to solidify your understanding. We'll also delve into the broader concept of LCM and its significance in various mathematical contexts.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. Understanding LCM is crucial for various mathematical operations, including simplifying fractions, solving problems involving ratios and proportions, and even scheduling tasks with cyclical patterns. This guide focuses on efficiently calculating the LCM of 30 and 48, illustrating multiple approaches along the way.
Method 1: Listing Multiples
The most straightforward, albeit potentially time-consuming method, is listing the multiples of each number until a common multiple is found.
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, ...
- Multiples of 48: 48, 96, 144, 192, 240, ...
By comparing the lists, we observe that the smallest common multiple is 240. Therefore, the LCM(30, 48) = 240. This method works well for smaller numbers but becomes impractical for larger numbers.
Method 2: Prime Factorization
This method is more efficient and systematic, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in either factorization.
-
Prime Factorization of 30:
30 = 2 × 15 = 2 × 3 × 5
-
Prime Factorization of 48:
48 = 2 × 24 = 2 × 2 × 12 = 2 × 2 × 2 × 6 = 2 × 2 × 2 × 2 × 3 = 2<sup>4</sup> × 3
-
Constructing the LCM:
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2<sup>4</sup> = 16
- The highest power of 3 is 3<sup>1</sup> = 3
- The highest power of 5 is 5<sup>1</sup> = 5
Therefore, LCM(30, 48) = 2<sup>4</sup> × 3 × 5 = 16 × 3 × 5 = 240.
This method is generally preferred because it's less prone to error and scales well for larger numbers. The prime factorization method provides a deeper understanding of the numbers' structure and their relationship.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula connecting them:
LCM(a, b) × GCD(a, b) = a × b
where 'a' and 'b' are the two numbers.
-
Finding the GCD of 30 and 48:
We can use the Euclidean algorithm to find the GCD.
- 48 = 30 × 1 + 18
- 30 = 18 × 1 + 12
- 18 = 12 × 1 + 6
- 12 = 6 × 2 + 0
The last non-zero remainder is 6, so GCD(30, 48) = 6.
-
Using the formula:
LCM(30, 48) = (30 × 48) / GCD(30, 48) = (30 × 48) / 6 = 1440 / 6 = 240.
This method is efficient if you already know or can easily calculate the GCD of the two numbers. The Euclidean algorithm is a particularly robust method for finding the GCD of even very large numbers.
Method 4: Ladder Method (or Staircase Method)
This visual method is helpful for understanding the concept of finding the LCM. We arrange the numbers in a ladder-like structure and repeatedly divide by common factors until we are left with only 1s. The LCM is then the product of all the divisors used.
2 | 30 48
2 | 15 24
2 | 15 12
2 | 15 6
3 | 15 3
5 | 5 1
| 1 1
LCM = 2 × 2 × 2 × 2 × 3 × 5 = 240
This method visually represents the prime factorization process, making it easier to follow for beginners.
Explanation of Prime Factorization and its Importance in LCM Calculation
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely expressed as a product of prime numbers (ignoring the order of the factors).
Prime factorization is crucial for finding the LCM because it allows us to systematically identify all the prime factors contributing to the multiples of the given numbers. By taking the highest power of each prime factor present in the factorizations, we ensure that the resulting LCM will be divisible by both numbers and the smallest such multiple.
Applications of LCM in Real-world Scenarios
The concept of LCM has numerous applications beyond theoretical mathematics. Here are a few examples:
-
Scheduling: Imagine two buses depart from a station at different intervals. One bus leaves every 30 minutes, and another every 48 minutes. Using the LCM, you can determine when both buses will depart simultaneously again (after 240 minutes, or 4 hours).
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is necessary when adding or subtracting fractions with unlike denominators. This ensures that you have a common denominator for performing the operation.
-
Gear Ratios: In mechanical engineering, gear ratios often involve finding the LCM to determine the synchronization of rotating parts in machines.
-
Cyclic Patterns: Many real-world events follow cyclical patterns (e.g., planetary orbits, tides). LCM helps analyze and predict when these patterns will coincide.
Frequently Asked Questions (FAQ)
-
Q: Is the LCM always larger than the two given numbers?
A: Yes, the LCM will always be greater than or equal to the larger of the two numbers. It will be equal only if one number is a multiple of the other.
-
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the prime factorization method to include all the numbers. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations to construct the LCM.
-
Q: Can the LCM be negative?
A: No, the LCM is always a positive integer.
-
Q: Is there a formula for the LCM of more than two numbers?
A: There isn't a single, simple formula like the one for two numbers. The process involves iterative calculation using the prime factorization method or similar approaches, extending the principle to accommodate additional numbers.
-
Q: Why is the prime factorization method considered the most efficient?
A: The prime factorization method is considered the most efficient because it directly addresses the fundamental structure of the numbers involved. It systematically identifies all the prime factors and their powers, guaranteeing a correct and efficient calculation, especially when dealing with larger numbers. Other methods, while useful for smaller numbers, become cumbersome and more prone to error as the numbers increase in size.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with various practical applications. We've explored four different methods for calculating the LCM of 30 and 48, highlighting the efficiency and underlying principles of each approach. The prime factorization method stands out as the most robust and generalizable technique, particularly suitable for handling larger numbers and more complex scenarios. Understanding the LCM enhances your mathematical abilities and problem-solving skills, making it a valuable tool in diverse fields. Remember to practice these methods with different number pairs to solidify your understanding and develop proficiency in calculating LCMs.
Latest Posts
Latest Posts
-
2000 In Words For Check
Sep 25, 2025
-
Whats The Factors Of 20
Sep 25, 2025
-
Is 7 An Even Number
Sep 25, 2025
-
What Words Start With Mashed
Sep 25, 2025
-
Is Prime Odd Or Even
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 30 And 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.