Lcm Of 3 And 18
seoindie
Sep 23, 2025 · 6 min read
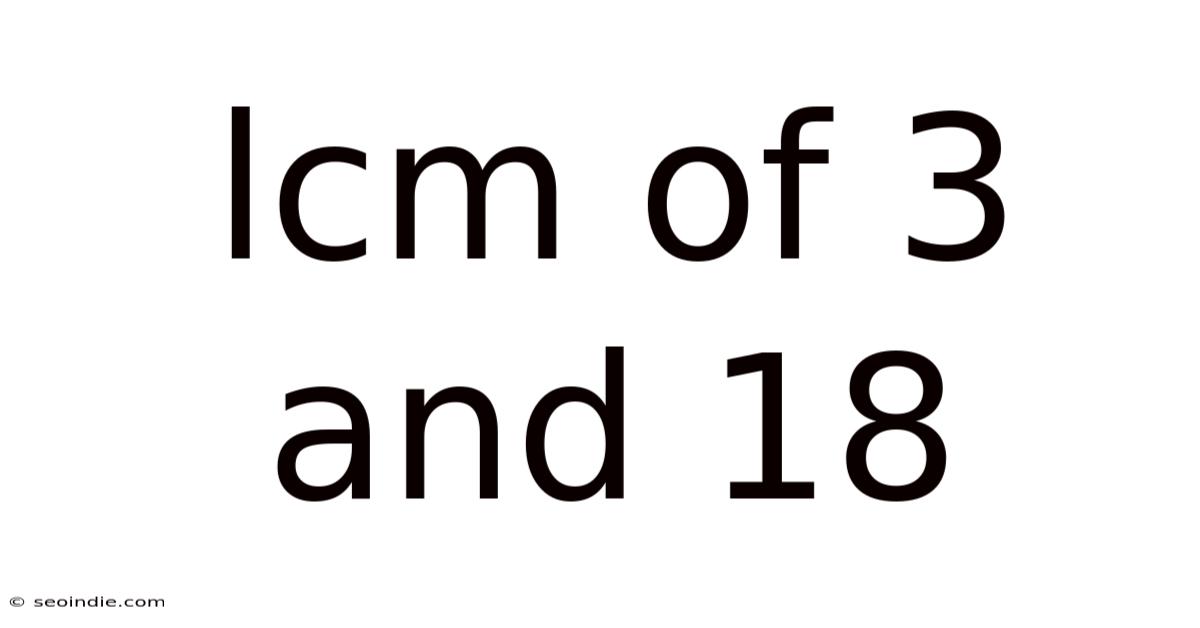
Table of Contents
Unveiling the Least Common Multiple (LCM) of 3 and 18: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical applications. This comprehensive guide delves into calculating the LCM of 3 and 18, exploring multiple methods and illuminating the broader significance of LCM in various mathematical contexts. We’ll go beyond a simple answer, examining the theoretical underpinnings and practical uses of this fundamental concept.
Understanding Least Common Multiple (LCM)
Before we dive into the specifics of finding the LCM of 3 and 18, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. This concept is crucial in various areas, from simplifying fractions to solving problems involving cycles and patterns.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of relatively small numbers like 3 and 18 is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27…
- Multiples of 18: 18, 36, 54, 72…
By comparing the lists, we can see that the smallest number appearing in both lists is 18. Therefore, the LCM of 3 and 18 is 18.
Method 2: Prime Factorization
Prime factorization offers a more systematic and efficient approach, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 3: 3 is a prime number, so its prime factorization is simply 3.
-
Prime Factorization of 18: 18 can be broken down as follows: 18 = 2 x 9 = 2 x 3 x 3 = 2 x 3².
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together. In this case, the prime factors are 2 and 3. The highest power of 2 is 2¹ and the highest power of 3 is 3².
Therefore, LCM(3, 18) = 2¹ x 3² = 2 x 9 = 18.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The GCD is the largest number that divides both integers without leaving a remainder. There's a convenient formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Finding the GCD of 3 and 18: The GCD of 3 and 18 is 3 because 3 is the largest number that divides both 3 and 18 evenly.
-
Applying the formula: LCM(3, 18) = (|3 x 18|) / GCD(3, 18) = 54 / 3 = 18.
Why is understanding LCM important?
The concept of LCM extends far beyond simple arithmetic exercises. Its applications span various fields:
-
Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/3 and 1/18, we find the LCM of 3 and 18 (which is 18), then convert the fractions to equivalent fractions with a denominator of 18 before adding them.
-
Scheduling and Cyclical Events: LCM is invaluable in scheduling problems. Imagine two buses that depart from the same station, one every 3 minutes and the other every 18 minutes. The LCM (18 minutes) determines when both buses will depart simultaneously again. This concept applies to various cyclical processes, from planetary alignments to machine maintenance schedules.
-
Modular Arithmetic: In modular arithmetic (a system of arithmetic for integers), the LCM plays a crucial role in solving congruences and determining when certain patterns repeat.
-
Music Theory: The LCM is used in music theory to determine the least common multiple of the durations of musical notes, helping in calculating rhythmic patterns and harmonies.
-
Abstract Algebra: The concept of LCM extends to more advanced mathematical structures like rings and fields, where the concept of least common multiple is generalized to ideals and other algebraic objects.
Further Exploration: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For the prime factorization method, we would simply include all the prime factors from all the numbers, taking the highest power of each. For the GCD method, we would need to extend the formula iteratively. For example, to find the LCM of 3, 6, and 18:
-
Prime Factorization:
- 3 = 3¹
- 6 = 2¹ x 3¹
- 18 = 2¹ x 3²
-
LCM: The highest power of 2 is 2¹, and the highest power of 3 is 3². Therefore, LCM(3, 6, 18) = 2¹ x 3² = 18.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If two or more numbers are relatively prime (they share no common factors other than 1), their LCM is simply the product of the numbers. For example, LCM(5, 7) = 5 x 7 = 35.
Q: Can the LCM be larger than the product of the numbers?
A: No. The LCM will always be less than or equal to the product of the numbers. In the case where the numbers are relatively prime, the LCM equals the product.
Q: Is there a single "best" method for finding the LCM?
A: The best method depends on the numbers involved. For small numbers, listing multiples is easy. For larger numbers, prime factorization is more efficient. The GCD method is useful when you already know the GCD.
Q: How can I use a calculator to find the LCM?
A: Many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers. Refer to your calculator's manual for instructions.
Conclusion
Finding the LCM of 3 and 18, whether through listing multiples, prime factorization, or using the GCD, consistently yields the answer 18. This seemingly simple calculation underscores the importance of understanding fundamental mathematical concepts and their diverse applications. The LCM is not merely an abstract idea but a practical tool with far-reaching implications across various fields, demonstrating the interconnectedness of mathematical principles and their relevance to the real world. Mastering the LCM calculation opens doors to a deeper appreciation of mathematics and its power to solve problems in unexpected ways.
Latest Posts
Latest Posts
-
The Vltage Valur At Which
Sep 23, 2025
-
First 20 Elements Electronic Configuration
Sep 23, 2025
-
Gcf Of 45 And 25
Sep 23, 2025
-
Adjectives To Describe A Tree
Sep 23, 2025
-
Meaning Of Non Biodegradable Waste
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.