Lcm Of 24 And 27
seoindie
Sep 17, 2025 · 6 min read
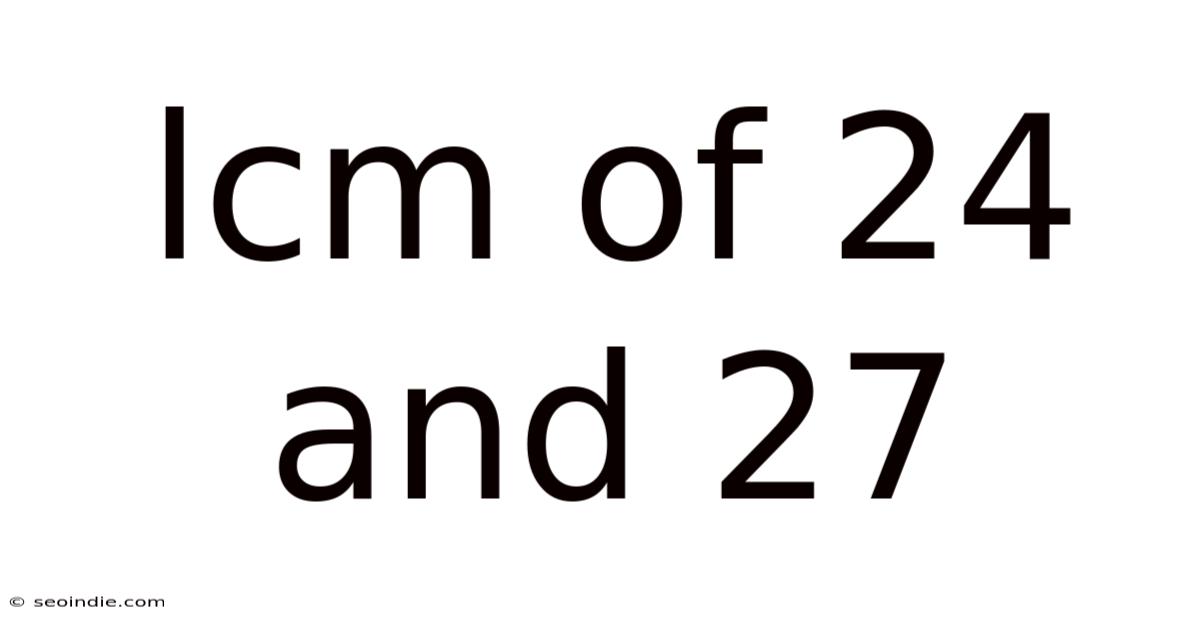
Table of Contents
Finding the LCM of 24 and 27: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will delve into the process of finding the LCM of 24 and 27, exploring different methods and providing a deeper understanding of the underlying mathematical principles. We'll cover everything from basic definitions to advanced techniques, ensuring you grasp this concept thoroughly.
What is the Least Common Multiple (LCM)?
Before we dive into calculating the LCM of 24 and 27, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the factors of both numbers. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method, particularly useful for smaller numbers like 24 and 27, involves listing the multiples of each number until you find the smallest multiple they share.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, ...
- Multiples of 27: 27, 54, 81, 108, 135, 162, 189, 216, ...
By comparing the lists, we can see that the smallest number present in both lists is 216. Therefore, the LCM of 24 and 27 is 216. This method is simple but can become cumbersome when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Find the prime factorization of 24.
24 can be factored as: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
Step 2: Find the prime factorization of 27.
27 can be factored as: 27 = 3 x 3 x 3 = 3³
Step 3: Identify the highest power of each prime factor.
In the prime factorizations of 24 and 27, we have the prime factors 2 and 3. The highest power of 2 is 2³ (from 24), and the highest power of 3 is 3³ (from 27).
Step 4: Multiply the highest powers together.
To find the LCM, multiply the highest powers of each prime factor: 2³ x 3³ = 8 x 27 = 216
Therefore, the LCM of 24 and 27 is 216 using the prime factorization method. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers, and GCD(a, b) is their greatest common divisor.
Step 1: Find the GCD of 24 and 27 using the Euclidean algorithm.
The Euclidean algorithm is an efficient method for finding the GCD.
- Divide the larger number (27) by the smaller number (24): 27 = 24 x 1 + 3
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (3): 24 = 3 x 8 + 0
The last non-zero remainder is the GCD, which is 3.
Step 2: Apply the formula.
LCM(24, 27) = (24 x 27) / GCD(24, 27) = (24 x 27) / 3 = 648 / 3 = 216
Therefore, the LCM of 24 and 27 is 216 using the GCD method. This method demonstrates the elegant relationship between LCM and GCD.
Understanding the Significance of LCM
The LCM has wide-ranging applications in various mathematical and real-world contexts. Here are a few examples:
- Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling: Determining when events will occur simultaneously (e.g., buses arriving at the same stop) involves finding the LCM of the time intervals.
- Cyclic patterns: Identifying when repeating patterns will coincide requires finding the LCM of the cycle lengths.
- Modular arithmetic: LCM plays a critical role in solving congruences and other problems in modular arithmetic.
A Deeper Dive into Prime Factorization
The prime factorization method offers a powerful understanding of the underlying structure of numbers. It reveals the fundamental building blocks of a number and allows for efficient calculation of LCM and GCD. Let's revisit the prime factorization of 24 and 27:
24 = 2³ x 3¹ 27 = 3³
Notice that the LCM includes all the prime factors, with each factor raised to its highest power. This is because the LCM must be divisible by both numbers, hence it must contain all their prime factors.
Addressing Common Misconceptions
A common mistake is confusing LCM with GCD. Remember:
- LCM: The smallest number divisible by both numbers.
- GCD: The largest number that divides both numbers.
Another misconception involves assuming the LCM is always the product of the two numbers. This is only true if the GCD of the two numbers is 1 (they are relatively prime).
Frequently Asked Questions (FAQ)
-
Q: Is there a way to find the LCM of more than two numbers?
- A: Yes, the prime factorization method extends easily to more than two numbers. Find the prime factorization of each number, then take the highest power of each prime factor present and multiply them together.
-
Q: Can the LCM of two numbers be smaller than both numbers?
- A: No, the LCM is always greater than or equal to the larger of the two numbers.
-
Q: What if one of the numbers is zero?
- A: The LCM of any number and zero is undefined.
-
Q: Are there any shortcuts for finding the LCM?
- A: If you notice that the numbers share no common factors (their GCD is 1), then their LCM is simply their product.
Conclusion
Finding the least common multiple is a valuable skill with applications in numerous areas of mathematics and beyond. We've explored three different methods – listing multiples, prime factorization, and using the GCD – each offering a unique perspective on this fundamental concept. The prime factorization method, in particular, provides a deep understanding of the underlying number theory principles. Remember to choose the method that best suits the numbers you're working with and always double-check your calculations. Mastering the LCM lays a strong foundation for tackling more advanced mathematical concepts. Understanding the relationship between LCM and GCD enhances problem-solving skills and opens up a wider appreciation of number theory. By understanding the different approaches and the underlying theory, you can confidently tackle LCM problems of any complexity.
Latest Posts
Latest Posts
-
Linear Equations Consistent Or Inconsistent
Sep 17, 2025
-
How To Find Average Revenue
Sep 17, 2025
-
List Of Factors 1 100
Sep 17, 2025
-
Calculating Polar Moment Of Inertia
Sep 17, 2025
-
Are Fungi Prokaryotic Or Eukaryotic
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.