Lcm Of 24 And 16
seoindie
Sep 17, 2025 · 6 min read
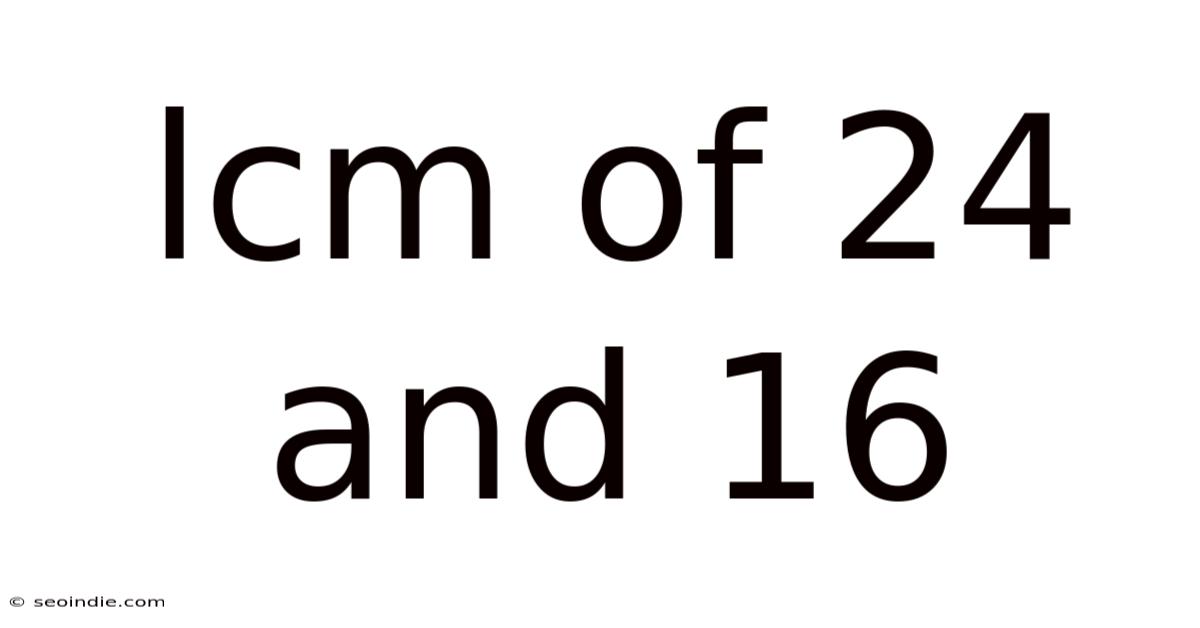
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 16: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 24 and 16, is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will walk you through different methods to calculate the LCM of 24 and 16, providing a deep understanding of the underlying principles and demonstrating their practical use. We'll cover everything from basic methods to more advanced techniques, ensuring you master this essential mathematical skill.
Understanding Least Common Multiple (LCM)
Before diving into the calculations, let's establish a clear understanding of what the LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, if we consider the numbers 2 and 3, their LCM is 6 because 6 is the smallest number divisible by both 2 and 3.
Think of it like this: Imagine you have two gears with different numbers of teeth (24 and 16 teeth, in our case). The LCM represents the smallest number of rotations needed for both gears to return to their starting positions simultaneously. This analogy highlights the practical relevance of LCM in scenarios involving cyclical processes.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 24 and 16:
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240, ...
- Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, ...
By comparing the lists, we can see that the smallest number that appears in both lists is 48. Therefore, the LCM of 24 and 16 is 48. This method is simple for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
- Prime factorization of 16: 16 = 2 x 2 x 2 x 2 = 2⁴
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(24, 16) = 2⁴ x 3¹ = 16 x 3 = 48
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic approach that eliminates the need for extensive listing.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a handy formula that connects the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
First, we need to find the GCD of 24 and 16. We can use the Euclidean algorithm for this:
- Divide the larger number (24) by the smaller number (16): 24 ÷ 16 = 1 with a remainder of 8.
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (8): 16 ÷ 8 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 8.
Now, we can use the formula:
LCM(24, 16) = (24 x 16) / 8 = 384 / 8 = 48
This method is also efficient and demonstrates the relationship between LCM and GCD, providing a deeper understanding of number theory concepts.
Method 4: Ladder Method (or Staircase Method)
This visual method helps understand the prime factorization approach in a more intuitive way. Let's apply it to 24 and 16:
2 | 24 16
2 | 12 8
2 | 6 4
2 | 3 2
3 | 3 1
---| --- ---
1 1
We start by dividing both numbers by the smallest prime number that divides at least one of them (2). We continue this process until we get 1 for both numbers. Then we multiply the prime numbers on the left-hand side to obtain the LCM: 2 x 2 x 2 x 2 x 3 = 48. This method is particularly helpful for visualizing the process and reinforcing the concept of prime factorization.
The Significance of LCM in Real-World Applications
The LCM is not just a theoretical concept; it has numerous practical applications:
- Scheduling: Imagine two buses leaving a terminal at different intervals. The LCM helps determine when both buses will depart simultaneously again.
- Fraction Addition and Subtraction: Finding the LCM of the denominators is crucial for adding or subtracting fractions with different denominators.
- Cyclic Processes: LCM finds use in scenarios involving periodic events, like the synchronization of machines or the alignment of celestial bodies.
- Project Management: Determining the least common multiple of task durations can help optimize project timelines.
- Music Theory: LCM plays a role in understanding musical intervals and harmonies.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined because 0 is not a factor of any positive integer.
Q: Can I use this method for more than two numbers?
A: Yes, the prime factorization method can be extended to find the LCM of more than two numbers. You would still find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations.
Q: Is there a way to find the LCM of very large numbers efficiently?
A: For extremely large numbers, advanced algorithms based on the Euclidean algorithm and other number theory concepts are employed to efficiently compute the GCD and, consequently, the LCM.
Q: Why is the prime factorization method considered more efficient?
A: The listing method relies on brute-force searching, while prime factorization provides a structured approach that reduces the search space significantly, especially for larger numbers.
Conclusion
Finding the LCM of 24 and 16, as we've demonstrated, can be accomplished through several methods: listing multiples, prime factorization, using the GCD, and the ladder method. While the listing method is intuitive for small numbers, the prime factorization and GCD methods are more efficient and adaptable to larger numbers. Understanding these methods not only allows you to calculate the LCM but also enhances your comprehension of fundamental mathematical concepts and their real-world applications. Mastering LCM calculation is a crucial step in building a solid foundation in mathematics, opening doors to more advanced concepts and problem-solving skills. Remember to choose the method that best suits your needs and understanding, and don't hesitate to explore the different approaches to solidify your grasp of this important mathematical concept.
Latest Posts
Latest Posts
-
Example Of An Unsaturated Hydrocarbon
Sep 17, 2025
-
Organisms In The Kingdom Protista
Sep 17, 2025
-
What Times What Equals 68
Sep 17, 2025
-
Lcm Of 7 6 3
Sep 17, 2025
-
Lcm Of 11 And 7
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.