Lcm Of 21 And 6
seoindie
Sep 13, 2025 · 6 min read
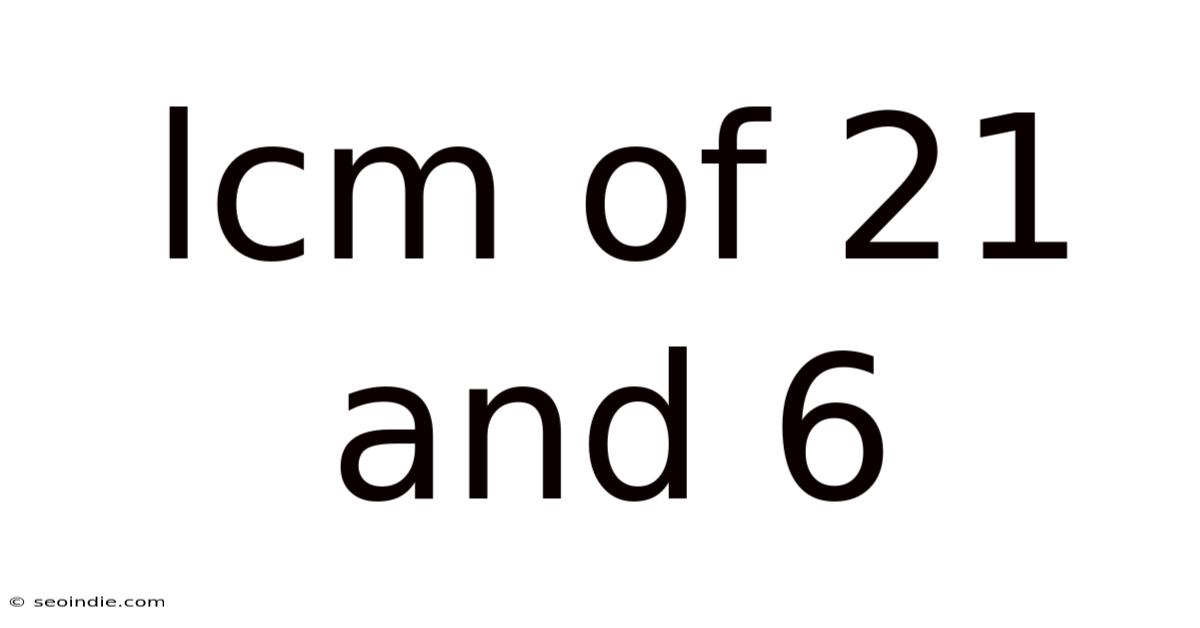
Table of Contents
Finding the Least Common Multiple (LCM) of 21 and 6: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial for working with fractions and solving various mathematical problems. This article provides a comprehensive guide to calculating the LCM of 21 and 6, exploring different methods and delving into the underlying mathematical principles. Understanding LCMs is essential for students across various grade levels, from elementary school to higher education, and is frequently applied in fields like engineering, computer science, and music theory. We’ll not only show you how to find the LCM of 21 and 6 but also equip you with the knowledge to tackle similar problems effectively.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 21 and 6, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving any remainder. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This method is particularly useful for smaller numbers like 21 and 6. We list the multiples of each number until we find the smallest common multiple.
Multiples of 21: 21, 42, 63, 84, 105, 126, ...
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, ...
Notice that 42 appears in both lists. Since it's the smallest number common to both lists, the LCM of 21 and 6 is 42. This method is straightforward but can become cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Prime factorization of 21:
21 = 3 x 7
Prime factorization of 6:
6 = 2 x 3
Now, let's construct the LCM:
- We have the prime factors 2, 3, and 7.
- The highest power of 2 is 2¹ (from the prime factorization of 6).
- The highest power of 3 is 3¹ (present in both factorizations).
- The highest power of 7 is 7¹ (from the prime factorization of 21).
Therefore, the LCM(21, 6) = 2¹ x 3¹ x 7¹ = 2 x 3 x 7 = 42.
Method 3: Using the Formula (for two numbers)
For two numbers 'a' and 'b', the LCM can be calculated using the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where GCD(a, b) is the greatest common divisor (highest common factor) of 'a' and 'b'.
First, we need to find the GCD of 21 and 6. We can use the Euclidean algorithm for this:
- 21 = 3 x 6 + 3
- 6 = 2 x 3 + 0
The last non-zero remainder is 3, so GCD(21, 6) = 3.
Now, we can apply the formula:
LCM(21, 6) = (|21 x 6|) / 3 = 126 / 3 = 42
Therefore, the LCM of 21 and 6 is 42, confirming the results obtained using the previous methods.
Explanation of the Formula: LCM and GCD Relationship
The formula LCM(a, b) = (|a x b|) / GCD(a, b) stems from a fundamental relationship between the LCM and GCD of two numbers. Consider the prime factorizations of 'a' and 'b':
- a = p₁^α₁ * p₂^α₂ * ... * pₙ^αₙ
- b = p₁^β₁ * p₂^β₂ * ... * pₙ^βₙ
Where p₁, p₂, ..., pₙ are prime numbers and αᵢ and βᵢ are their respective exponents.
The GCD(a, b) is found by taking the minimum exponent for each prime factor:
GCD(a, b) = p₁^min(α₁, β₁) * p₂^min(α₂, β₂) * ... * pₙ^min(αₙ, βₙ)
The LCM(a, b) is found by taking the maximum exponent for each prime factor:
LCM(a, b) = p₁^max(α₁, β₁) * p₂^max(α₂, β₂) * ... * pₙ^max(αₙ, βₙ)
Now, consider the product of 'a' and 'b':
a x b = p₁^(α₁+β₁) * p₂^(α₂+β₂) * ... * pₙ^(αₙ+βₙ)
Notice that min(αᵢ, βᵢ) + max(αᵢ, βᵢ) = αᵢ + βᵢ for each i. This relationship underpins the formula, allowing us to efficiently compute the LCM using the GCD.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
-
Scheduling Problems: LCM is useful in solving scheduling problems. For example, if two events occur at regular intervals, the LCM helps determine when both events will coincide.
-
Music Theory: LCM plays a role in understanding musical intervals and harmonies.
-
Gear Ratios: In mechanics, LCM helps calculate gear ratios and speeds.
-
Computer Science: LCM finds applications in algorithms and data structures.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers are negative?
- A: The formula works with the absolute values of the numbers. The LCM itself will always be positive.
-
Q: Can this method be used for more than two numbers?
- A: Yes, the prime factorization method can be extended to find the LCM of more than two numbers. You find the prime factorization of each number and then construct the LCM using the highest power of each prime factor present. The formula method, however, needs to be adapted for more than two numbers; iterative application of the formula is required.
-
Q: Is there a difference between finding the LCM and finding the GCD?
- A: Yes, the LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related but represent different aspects of the number relationships.
-
Q: Why is the LCM important in fraction operations?
- A: When adding or subtracting fractions, having a common denominator simplifies the process significantly. The LCM provides the smallest possible common denominator.
-
Q: Are there any online calculators or tools available to find the LCM?
- A: Yes, numerous online calculators are available that can quickly compute the LCM of multiple numbers. These tools are very helpful for verifying your calculations or for dealing with larger numbers.
Conclusion
Finding the least common multiple is a vital skill in mathematics. We explored three different methods for calculating the LCM of 21 and 6: listing multiples, prime factorization, and using the formula relating the LCM and GCD. The prime factorization method is generally the most efficient, especially for larger numbers, while the formula method provides a concise and elegant approach. Understanding the underlying principles and the relationship between LCM and GCD strengthens your mathematical foundation and equips you to confidently tackle a wide range of mathematical problems. Remember to choose the method that best suits the numbers you are working with and the context of the problem. The LCM, seemingly a simple concept, finds its application in numerous fields, highlighting its importance in both theoretical and practical mathematics.
Latest Posts
Latest Posts
-
How To Spell Number 15
Sep 13, 2025
-
1 Percent Of 1 Billion
Sep 13, 2025
-
What Numbers Go Into 36
Sep 13, 2025
-
12 Inches In A Foot
Sep 13, 2025
-
How Do You Spell 81
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 21 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.