Lcm Of 20 And 35
seoindie
Sep 20, 2025 · 6 min read
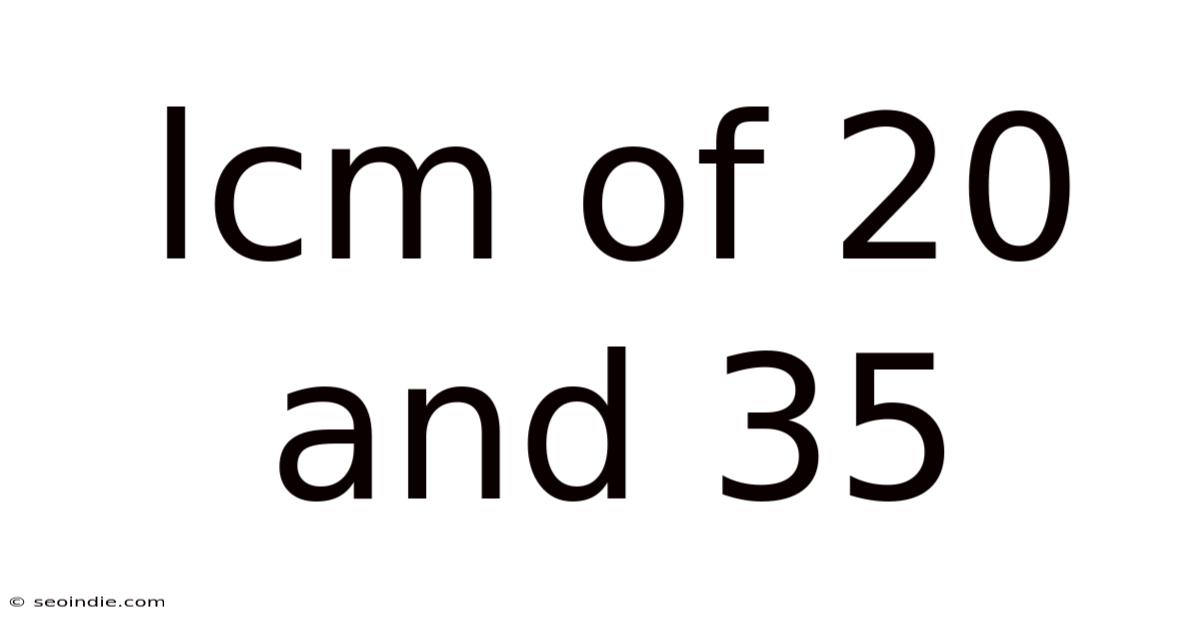
Table of Contents
Understanding the Least Common Multiple (LCM) of 20 and 35: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for grasping more advanced mathematical principles. This article delves deep into finding the LCM of 20 and 35, explaining multiple approaches, exploring the theoretical background, and providing practical examples to solidify your understanding. This guide is perfect for students, teachers, and anyone looking to refresh their knowledge of LCM and its applications.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding the LCM is fundamental in various mathematical applications, including simplifying fractions, solving problems involving time and cycles, and working with ratios and proportions. This guide will focus on finding the LCM of 20 and 35, demonstrating various methods and illuminating the underlying principles.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 20 and 35:
- Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, ...
- Multiples of 35: 35, 70, 105, 140, 175, 210, ...
By comparing the lists, we can see that the smallest multiple common to both 20 and 35 is 140. Therefore, the LCM(20, 35) = 140. This method is effective for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the LCM's structure. It involves breaking down each number into its prime factors. Prime factorization is expressing a number as a product of its prime numbers (numbers divisible only by 1 and themselves).
Let's find the prime factorization of 20 and 35:
- 20 = 2² × 5 (20 is 2 multiplied by 2 multiplied by 5)
- 35 = 5 × 7 (35 is 5 multiplied by 7)
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
- The prime factors are 2, 5, and 7.
- The highest power of 2 is 2² = 4.
- The highest power of 5 is 5¹ = 5.
- The highest power of 7 is 7¹ = 7.
Therefore, LCM(20, 35) = 2² × 5 × 7 = 4 × 5 × 7 = 140
This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or multiple numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD), also known as the greatest common factor (GCF), are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides another method for calculating the LCM.
First, let's find the GCD of 20 and 35 using the Euclidean algorithm:
- Divide the larger number (35) by the smaller number (20): 35 ÷ 20 = 1 with a remainder of 15.
- Replace the larger number with the smaller number (20) and the smaller number with the remainder (15): 20 ÷ 15 = 1 with a remainder of 5.
- Repeat the process: 15 ÷ 5 = 3 with a remainder of 0.
- The last non-zero remainder is the GCD. In this case, the GCD(20, 35) = 5.
Now, using the relationship between LCM and GCD:
LCM(a, b) = (a × b) / GCD(a, b)
LCM(20, 35) = (20 × 35) / 5 = 700 / 5 = 140
This method is particularly useful when the GCD is easily determined, offering a quick alternative to prime factorization.
Understanding the Concepts: Why Does LCM Matter?
The LCM is not just a mathematical exercise; it has practical applications in various real-world scenarios. Consider these examples:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 20 minutes, and another arrives every 35 minutes. The LCM (140 minutes) helps determine when both buses will arrive simultaneously.
-
Fraction Operations: When adding or subtracting fractions, finding the LCM of the denominators is crucial to finding a common denominator. This simplifies the calculation and provides an accurate result.
-
Project Management: In project management, tasks might repeat at different intervals. Understanding LCM can aid in scheduling and coordinating tasks efficiently.
Real-world Applications of LCM
Beyond the simple examples, the LCM finds its application in more complex scenarios:
-
Gear Ratios: In mechanical engineering, understanding LCM helps determine the optimal gear ratios for smooth and efficient operation of machinery. The synchronization of rotating parts often relies on finding the LCM of their rotational speeds.
-
Signal Synchronization: In electronics and telecommunications, synchronizing signals often requires finding the LCM of signal frequencies. This ensures that signals are aligned and operate effectively together.
-
Cyclic Processes: Many natural and engineered systems operate in cycles. The LCM helps in analyzing the timing of events within these cycles and predicting when certain events will coincide.
-
Music Theory: In music theory, LCM plays a role in understanding musical intervals and harmonies. The relationships between note frequencies often involve multiples and common multiples.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for two numbers?
A: Yes, there's only one least common multiple for any given set of numbers. While there are infinitely many common multiples, only one is the smallest.
Q: What if the two numbers are relatively prime (their GCD is 1)?
A: If the GCD of two numbers is 1, their LCM is simply the product of the two numbers. For example, the LCM of 9 and 10 is 90 because their GCD is 1.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method or the GCD method to find the LCM of multiple numbers. For prime factorization, you consider all the prime factors and their highest powers present in any of the numbers' factorizations. For the GCD method, you can find the GCD of pairs of numbers sequentially and work your way up to the LCM of all the numbers.
Q: Can I use a calculator to find the LCM?
A: Most scientific calculators have a built-in function to calculate the LCM. Many online calculators are also available for this purpose.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill in mathematics with wide-ranging practical applications. While the simple listing method works for small numbers, the prime factorization and GCD methods are more efficient and provide a deeper understanding of the mathematical principles involved. Mastering these methods will not only improve your arithmetic skills but also enhance your ability to solve more complex problems in various fields, from scheduling to engineering. Remember the importance of understanding the underlying concepts, as this will solidify your understanding and prepare you for more advanced mathematical concepts. The LCM, although seemingly simple, is a powerful tool in the mathematician's arsenal, unlocking solutions to diverse and complex problems.
Latest Posts
Latest Posts
-
3 5 Centimeters In Inches
Sep 20, 2025
-
Hno2 Weak Or Strong Acid
Sep 20, 2025
-
What Times What Is 49
Sep 20, 2025
-
Nouns That Begin With V
Sep 20, 2025
-
Facotrs Of 180 In Pairs
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.